求4个数字组成的不重复三位数，Python解法

题目要求：
求所有由5,6,7,8组成的数字不重复的三位数

不重复的三位数，即不能出现555,566这种

通过分析，可以使用画树的方法来确定要求的三位数的值与个数

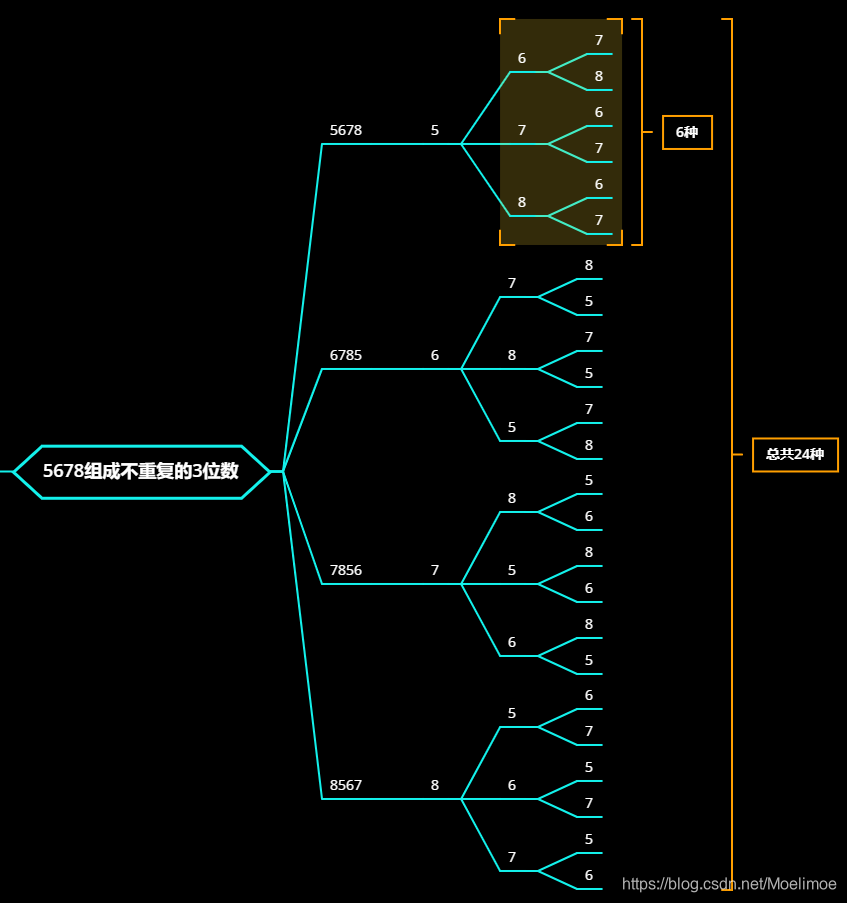
按照上图所示可以确定由5，6，7，8共可以组成24个不重复的三位数
于是写出Python代码如下：

class Solution:def noRepeatTriplets(self, strs='5678'):global nfirst, sub_str = strs[0], strs[1:]strs = sub_str + first  # 调换顺序用作下一轮运算时使用for i in range(len(sub_str)):for x in sub_str[:i] + sub_str[i + 1:]:s = first + sub_str[i] + xn += 1print(s, f'已输出次数：{n}')if strs == '5678':  # 再次回到5678则结束运算returnself.noRepeatTriplets(strs)n = 0
T = Solution()
T.noRepeatTriplets()

输出共24种：

567 已输出次数：1
568 已输出次数：2
576 已输出次数：3
578 已输出次数：4
586 已输出次数：5
587 已输出次数：6
678 已输出次数：7
675 已输出次数：8
687 已输出次数：9
685 已输出次数：10
657 已输出次数：11
658 已输出次数：12
785 已输出次数：13
786 已输出次数：14
758 已输出次数：15
756 已输出次数：16
768 已输出次数：17
765 已输出次数：18
856 已输出次数：19
857 已输出次数：20
865 已输出次数：21
867 已输出次数：22
875 已输出次数：23
876 已输出次数：24

时间复杂度和给出的数字位数d有关，两次for循环次数数量级都是d（都是循环d-1次），递归的次数也是d-1次，因此时间复杂度为O(d³)

以上方法也可以用于3位数或5位数，只需要将5678改成567或56789
如‘56789’（12×5=60种）：

class Solution:def noRepeatTriplets(self, strs='56789'):global nfirst, sub_str = strs[0], strs[1:]strs = sub_str + first  # 调换顺序用作下一轮运算时使用for i in range(len(sub_str)):for x in sub_str[:i] + sub_str[i + 1:]:s = first + sub_str[i] + xn += 1print(s, f'已输出次数：{n}')if strs == '56789':  # 再次回到56789则结束运算returnself.noRepeatTriplets(strs)n = 0
T = Solution()
T.noRepeatTriplets()

56789对应输出的60种不重复三位数：

567 已输出次数：1
568 已输出次数：2
569 已输出次数：3
576 已输出次数：4
578 已输出次数：5
...
976 已输出次数：56
978 已输出次数：57
985 已输出次数：58
986 已输出次数：59
987 已输出次数：60

这是我能想到的较容易理解的方法
如果你有更简单易懂的方法，欢迎一起评论交流