1.背包问题
(1)01背包
从n个重量和价值分别为wi,vi的物品,从中选出不超过W的物品,每种物品仅有一件,求所有方案中V的最大值。
最朴素最简单也最费时的方法:O(2^n) int rec(int i,int j)//从第i个开始挑选总重小于j的部分
递归 递归终止条件:i==n return 0;
递归分支:① j<wi res=rec(i+1,j); //无法挑选,看下一个
② res=max(rec(i+1,j),rec(i+1,j-w[i])+v[i]))//挑选,不挑选,选其中大的
分析:递归搜索深度→n,每层两次分支(选与不选),有重复计算
优化:记录每次递归的结果(记忆化搜索)
Int dp[MAX_N][MAX_N];
递归 int rec(int i,int j)
初始条件:memset(dp,-1,sizeof(dp));
终止条件:①dp[i][j]>=0 returndp[i][j]//已计算过
②i==n return 0;
递归分支:① j<wi res=rec(i+1,j); //无法挑选,看下一个
② res=max(rec(i+1,j),rec(i+1,j-w[i])+v[i]))//挑选,不挑选,选其中大的
分析及remark:复杂度O(nW)
数组初始化:①memset(type *arrary,figure,sizeof(arrary))
只能填充(0,+-1,0x3f3f3f3f),其他值不可以
memset按照1字节为单位对内存填充,-1的二进制每一位均为1
②fill(type* arrary,type *arrary+n,figure) 可赋值任意值
递归
↓↓↓↓↓↓ for(int i=n-1;i>=0;i--) //
递推(双重循环) for(int j=0;j<=w;j++)
{ if(j<w[i]) dp[i][j]=dp[i+1][j]; //不选
else dp[i][j]=max(dp[i+1][j],dp[i+1][j-w[i]]+v[i]);}
其他3种递推写法:(来源:《挑战程序设计竞赛》)
(2)完全背包
递推关系1:(3重循环,有重复计算)复杂度O(nW^2)
For(int i=0;i<n;i++)
For(int j=0;j<=w;j++)
For(int k=0;k*w[i]<=j;k++)
Dp[i+1][j]=max(dp[i+1][j],dp[i+1][j-k*w[i]]+k*v[i])
优化:(左上→右下 变为 左→右)
Dp数组初始化为0
For(int i=0;i<n;i++)
For(int j=0;j<=w;j++)
{
If(j<w[i]) dp[i+1][j]=dp[i][j];
Else dp[i+1][j]=max(dp[i][j],dp[i+1][j-w[i]]+v[i])
} 只有这里与01背包不同,前j个已更新过,可直接用
进一步优化:用一个数组实现,只需要记录当前最优状态
比较01背包与完全背包(循环方向不同)
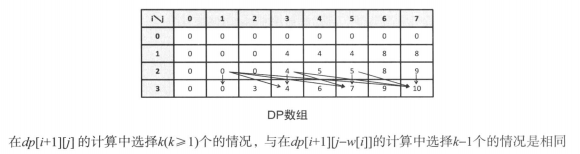
2.LCS(Longest common subsequence)
dp[n][m]即为所求
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
{
if(s[i]==t[i])
dp[i+1][j+1]=dp[i][j]+1;
else
dp[i+1][j+1]=max(dp[i+1][j],dp[i][j+1])
}
3.LIS(Longest Increasing subsequence)
dp[i]:以ai为结尾的最长上升子序列长度
dp[i]=max{1,dp[i]+1|j<i且aj<ai}
O(n^2)
int res;
for(int i=0;i<n;i++)
{
dp[i]=1;
for(int j=0;j<i;j++)
if(a[j]<a[i]) //每存在aj<ai&&j<i,dp[i]更新一次
dp[i]=max{dp[i],dp[j]+1};
}
res=max{dp[i]|0<=i<n}
Remark:
其他方法:
可以用lower_bound();
dp[i]:长度为i+1的上升子列中末尾元素的最小值(不存在的话为inf)
dp[max_n]初始化为inf,按顺序逐个考虑数列的元素,对于每个ai,如果i=0||dp[i-1]<ai,就用dp[i]=min(dp[i],ai)更新,最终找出使得dp[i]<inf的最大的i+1即为结果。DP直接实现,可以在O(n^2)的时间内给出结果,但可以进一步优化,dp数组中除inf之外是单调递增的,对于每个ai最多有一次更新,更新的位置可用二分的方法优化,时间复杂度可以降低到O(nlogn)
int dp[max_n]
void solve()
{
fill(dp,dp+n,inf);
for(int i=0;i<n;i++)
*lower_bound(dp,dp+n,a[i])=a[i];
res=lower_bound(dp,dp+n,inf)-dp;
}
// lower_bound()可以从已排好序的a中利用二分搜索找出满足ai>=k的ai的最小的指针,类似的还有upper_bound,找出的为ai>k的最小指针
//求n个有序数组a中k的个数,可以用:upper_bound(a,a+n,k)-lower_bound(a,a+n,k);










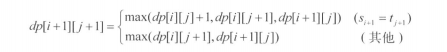







)

)




二叉树)




