前提要素

本文代码用Java实现。

//二叉树节点结构
public static class TreeNode {public int val;public TreeNode left;public TreeNode right;public TreeNode(int x) {val = x;}public TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}
}//打印二叉树节点值
private static void print(TreeNode node, StringBuilder sb) {sb.append(node.val);sb.append(',');
}

深度优先搜索DFS

经典遍历算法

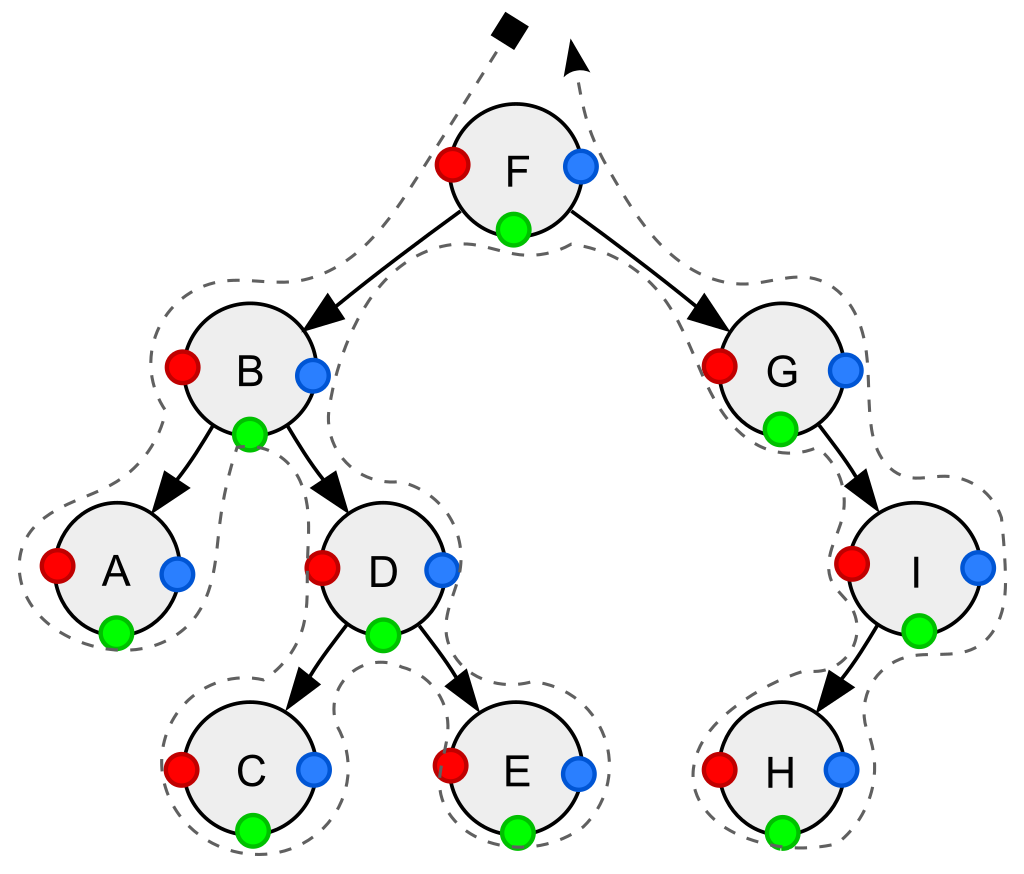
Depth-first traversal (dotted path) of a binary tree:

• Pre-order (node access at position red color dot):
  • F, B, A, D, C, E, G, I, H;
• In-order (node access at position green color dot):
  • A, B, C, D, E, F, G, H, I;
• Post-order (node access at position blue color dot):
  • A, C, E, D, B, H, I, G, F.

前序遍历

递归版

public static String recursivePreorderTraverse(TreeNode root) {if(root == null) return "";StringBuilder sb = new StringBuilder();recursivePreorderTraverse(root, sb);return sb.substring(0, sb.length() - 1);
}private static void recursivePreorderTraverse(TreeNode node, StringBuilder sb) {if (node == null)return;print(node, sb);recursivePreorderTraverse(node.left, sb);recursivePreorderTraverse(node.right, sb);
}

迭代版

public static String iterativePreorderTraverse(TreeNode root) {if(root == null)return "";StringBuilder sb = new StringBuilder();LinkedList<TreeNode> stack = new LinkedList<>();stack.push(root);while(!stack.isEmpty()) {TreeNode node = stack.pop();print(node, sb);//right child is pushed first so that left is processed firstif(node.right != null)stack.push(node.right);if(node.left != null)stack.push(node.left);}return sb.substring(0, sb.length() - 1);
}

中序遍历

递归版

public static String recursiveInorderTraverse(TreeNode root) {if(root == null) return "";StringBuilder sb = new StringBuilder();recursiveInorderTraverse(root, sb);return sb.substring(0, sb.length() - 1);
}private static void recursiveInorderTraverse(TreeNode node, StringBuilder sb) {if (node == null)return;recursiveInorderTraverse(node.left, sb);print(node, sb);recursiveInorderTraverse(node.right, sb);
}

迭代版

public static String iterativeInorderTraverse(TreeNode root) {if(root == null) return "";StringBuilder sb = new StringBuilder();LinkedList<TreeNode> stack = new LinkedList<>();TreeNode p = root;while(!stack.isEmpty() || p != null) {if(p != null) {stack.push(p);p = p.left;}else {p = stack.pop();print(p, sb);p = p.right;}}		return sb.substring(0, sb.length() - 1);
}

后序遍历

递归版

public static String recursivePostorderTraverse(TreeNode root) {if(root == null) return "";StringBuilder sb = new StringBuilder();recursivePostorderTraverse(root, sb);return sb.substring(0, sb.length() - 1);
}public static void recursivePostorderTraverse(TreeNode node, StringBuilder sb) {if (node == null)return;recursivePostorderTraverse(node.left, sb);recursivePostorderTraverse(node.right, sb);print(node, sb);
}

迭代版

public static String iterativePostorderTraverse(TreeNode root) {if(root == null) return "";StringBuilder sb = new StringBuilder();LinkedList<TreeNode> stack = new LinkedList<>();TreeNode p = root, lastNodeVisited = null;while(!stack.isEmpty() || p != null) {if(p != null) {stack.push(p);p = p.left;}else {TreeNode peekNode = stack.peek();// if right child exists and traversing node// from left child, then move rightif(peekNode.right != null && lastNodeVisited != peekNode.right) {p = peekNode.right;}else {print(peekNode, sb);lastNodeVisited = stack.pop();}}}return sb.substring(0, sb.length() - 1);
}

Morris遍历算法

实现二叉树的前序（preorder）、中序（inorder）、后序（postorder）遍历有两个常用的方法：一是递归（recursive），二是使用栈实现的迭代版本（stack+iterative）。这两种方法都是O(n)的空间复杂度（递归本身占用stack空间或者用户自定义的stack）。

Morris Traversal方法与前两种方法的不同在于该方法只需要O(1)空间，而且同样可以在O(n)时间内完成。

要使用O(1)空间进行遍历，最大的难点在于，遍历到子节点的时候怎样重新返回到父节点（假设节点中没有指向父节点的p指针），由于不能用栈作为辅助空间。为了解决这个问题，Morris方法用到了线索二叉树（threaded binary tree）的概念。在Morris方法中不需要为每个节点额外分配指针指向其前驱（predecessor）和后继节点（successor），只需要利用叶子节点中的左右空指针指向某种顺序遍历下的前驱节点或后继节点就可以了。

Morris只提供了中序遍历的方法，在中序遍历的基础上稍加修改可以实现前序遍历，后续遍历。

中序遍历

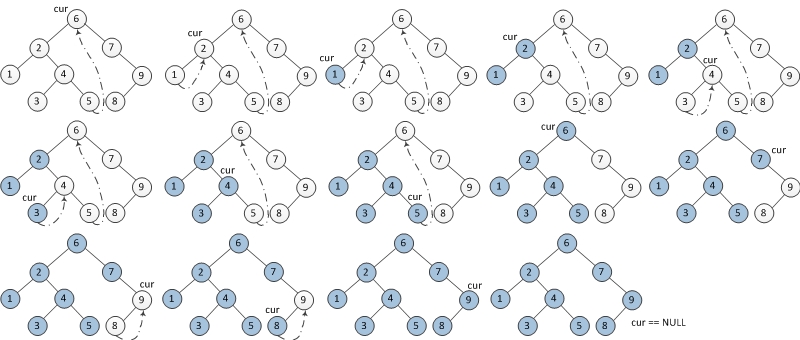
public String inorderTraverse(TreeNode root) {StringBuilder sb = new StringBuilder();inorderMorrisTraversal(root, sb);return sb.substring(0, sb.length() - 1);
}private void inorderMorrisTraversal(TreeNode root, StringBuilder sb) {TreeNode cur = root, prev = null;while (cur != null) {if (cur.left == null) {// 1.如果curr左子节点为空：print(cur.val, sb);// 输出当前节点cur = cur.right;// curr指向它的右子节点，为下次循环作准备} else {// 2. 如果curr左子节点不为空，在curr的左子树中，找到curr在中序遍历下的前驱节点。prev = cur.left;while (prev.right != null && prev.right != cur)prev = prev.right;// 2.a 如果前驱节点的右孩子为空，if (prev.right == null) {// （这里curr第一次遍历到，建立连接）prev.right = cur; // 将它的右子节点设置为curr。（让当前节点与中序遍历下的前驱节点形成链接，这里形成）cur = cur.left; // curr指向它的 左子节点，为下次循环作准备} else {// 2.b 如果前驱节点的右子节点 为curr，（这里curr第二次遍历到，断开连接，打印值）print(cur.val, sb);prev.right = null;// 将它的右孩子重新设为空（断开链接，恢复树的形状）。cur = cur.right; // curr指向它的 左子节点，为下次循环作准备}}}
}

前序遍历

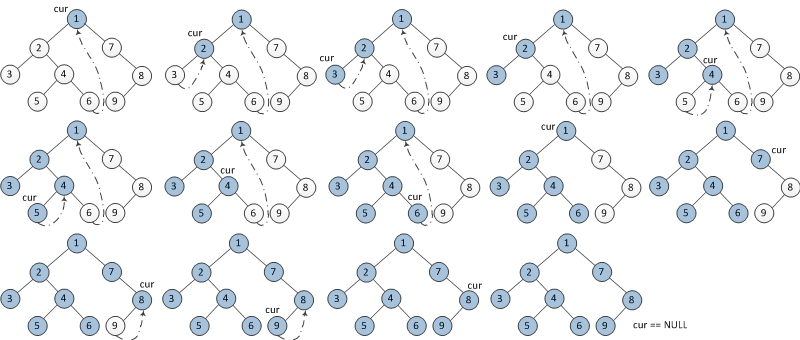
public String preorderTraverse(TreeNode root) {StringBuilder sb = new StringBuilder();preorderMorrisTraversal(root, sb);return sb.substring(0, sb.length() - 1);
}private void preorderMorrisTraversal(TreeNode root, StringBuilder sb) {TreeNode cur = root, prev = null;while (cur != null) {if (cur.left == null) {print(cur.val, sb);cur = cur.right;} else {prev = cur.left;while (prev.right != null && prev.right != cur)prev = prev.right;if (prev.right == null) {print(cur.val, sb); // the only difference with inorder-traversalprev.right = cur;cur = cur.left;} else {prev.right = null;cur = cur.right;}}}
}

后序遍历

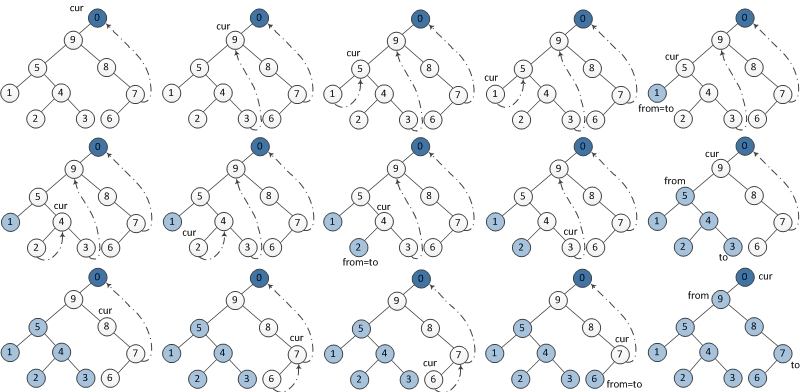
public String postorderTraverse(TreeNode root) {StringBuilder sb = new StringBuilder();postorderMorrisTraversal(root, sb);return sb.substring(0, sb.length() - 1);
}private void postorderMorrisTraversal(TreeNode root, StringBuilder sb) {TreeNode dump = new TreeNode(0);dump.left = root;TreeNode cur = dump, prev = null;while (cur != null) {if (cur.left == null) {cur = cur.right;} else {prev = cur.left;while (prev.right != null && prev.right != cur)prev = prev.right;if (prev.right == null) {prev.right = cur;cur = cur.left;} else {// call printprintReverse(cur.left, prev, sb); prev.right = null;cur = cur.right;}}}
}// print the reversed tree nodes 'from' -> 'to'
private void printReverse(TreeNode from, TreeNode to, StringBuilder sb) {reverse(from, to);TreeNode p = to;while (true) {print(p.val, sb);if (p == from)break;p = p.right;}reverse(to, from);
}// reverse the tree nodes 'from' -> 'to'.
private void reverse(TreeNode from, TreeNode to) {if (from == to)return;TreeNode x = from, y = from.right, z;while (true) {z = y.right;y.right = x;x = y;y = z;if (x == to)break;}
}

广度优先搜索BFS

按层遍历

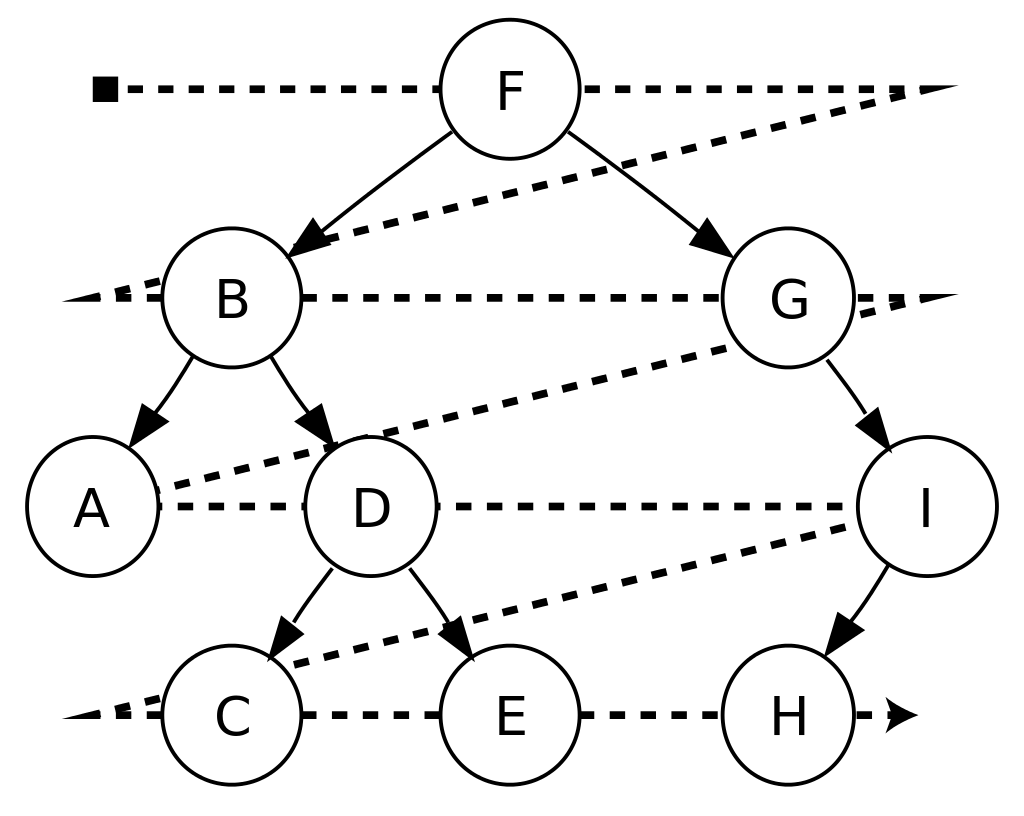
Level-order: F, B, G, A, D, I, C, E, H.

public static String levelOrderTraverse(TreeNode root) {if(root == null) return "";StringBuilder sb = new StringBuilder();LinkedList<TreeNode> queue = new LinkedList<>();queue.offer(root);while(!queue.isEmpty()) {TreeNode node = queue.poll();print(node, sb);if(node.left != null)queue.offer(node.left);if(node.right != null)queue.offer(node.right);}return sb.substring(0, sb.length() - 1);
}

参考资料

1. Tree traversal - Wikipedia
2. Morris Traversal方法遍历二叉树（非递归，不用栈，O(1)空间） - AnnieKim - 博客园