文章目录
- 题目
- 思路
- 代码
- 复杂度分析
题目
输入一个整数 n ，求1～n这n个整数的十进制表示中1出现的次数。
例如，输入12，那么1～12这些整数中包含1 的数字有1、10、11和12。可得1一共出现了5次。
思路
将个位、十位……每位1出现的次数加起来就是1一共出现的次数。
以12为例，个位上1出现了 2 次分别是 01，11（暂时不看11的十位）。
十位上1出现了 3 次，分别是10，11，12。
因此1~12中1一共出现了 2+3=5 次。
两位数不好找规律，我们以四位数为例。一个四位数十位上 1 出现的次数，与十位上的值有关。根据值不同，可分为三种情况，值为0，1，2~9：
我们通过三个不同四位数进行探讨，分别是 2304 ， 2314 和 2324 ：
我们将数字划分为三部分，当前位（cur），高位（high），以及低位（low），用digit表示当前处于哪个数位。
- 当
cur = 0时： 此位 1 的出现次数只由高位high决定，计算公式为：
high×digit
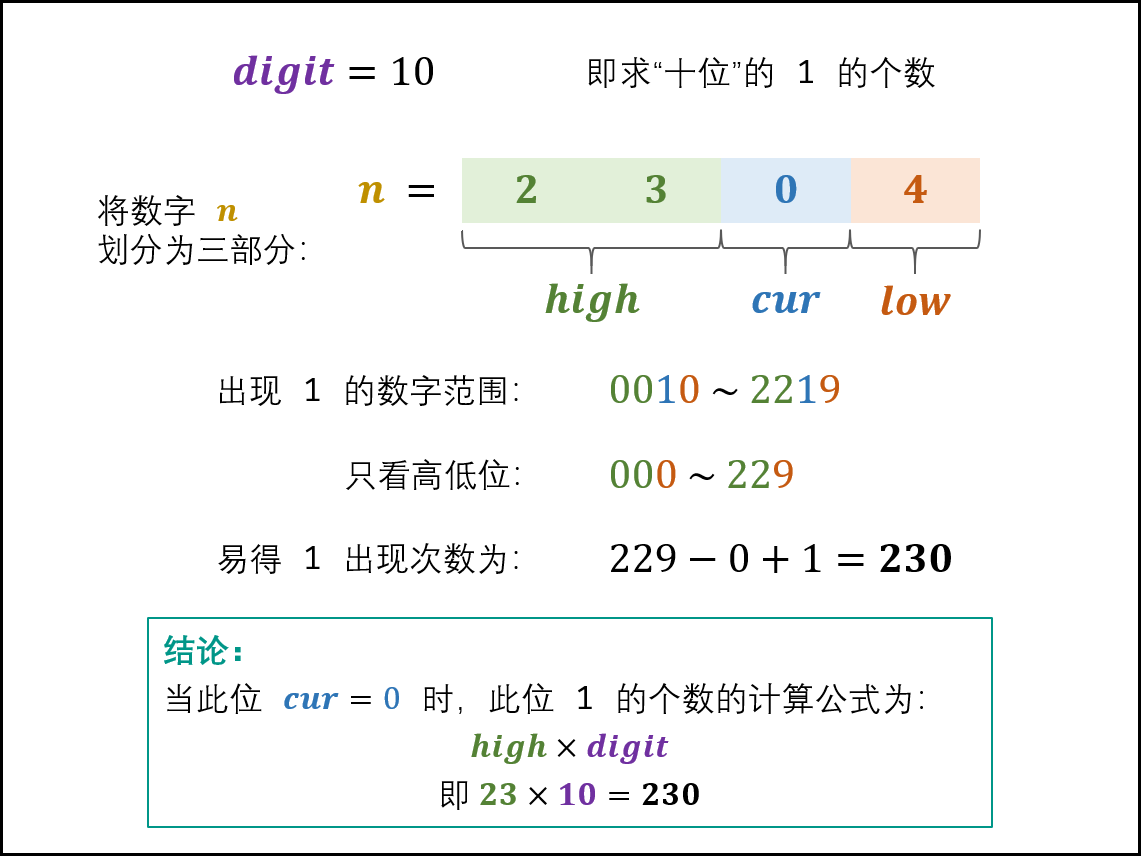
详细分析：
对于2304来讲，十位出现1的范围：0010~2219 没有什么可多说的。
那么1出现的次数怎么算呢？
光看高位的话，00 ~ 22 总共有 23 种数字，也就是 001X ~ 221X 。而其中的 ‘X'，有 0 ~ 9 总共 10 种取法，也就是说排列组合下来，可以构成有 23*10=230 个十位为1的数字，如下表：
| high | cur | low |
|---|---|---|
| 00 | 1 | 0 |
| 00 | 1 | 1 |
| 00 | 1 | 2 |
| 00 | 1 | 3 |
| 00 | 1 | 4 |
| 00 | 1 | 5 |
| 00 | 1 | 6 |
| 00 | 1 | 7 |
| 00 | 1 | 8 |
| 00 | 1 | 9 |
| … | 1 | … |
| 22 | 1 | 0 |
| 22 | 1 | 1 |
| 22 | 1 | 2 |
| 22 | 1 | 3 |
| 22 | 1 | 4 |
| 22 | 1 | 5 |
| 22 | 1 | 6 |
| 22 | 1 | 7 |
| 22 | 1 | 8 |
| 22 | 1 | 9 |
- 当
cur = 1时： 此位 1 的出现次数由高位high和低位low共同决定，计算公式为：
high×digit+low+1
详细分析：
十位上1出现的次数怎么算呢？
出现 1 的数字范围： 0010 ~ 2314
光看高位的话，有 00 ~ 23 总共 24 种组合排列方法，但是！ 对于 00 ~ 22 这 23 种高位来讲，低位都有 0 ~ 9 总共 10 种排列组合 —— 0010 ~ 0019 或 2210 ~ 2219 ，但是 23 不同，其低位只有 0 ~ 4 五种排列组合 —— 2310 ~ 2314 。因此，可以构成 23*10+5=235 个十位为 1 的数字（23*10代表 【高位为00~22】 的所有数字，5代表 【高位为23】 的所有数字）。
- 当
cur=2,3,⋯,9时： 此位 1 的出现次数只由高位high决定，计算公式为：
(high+1)×digit
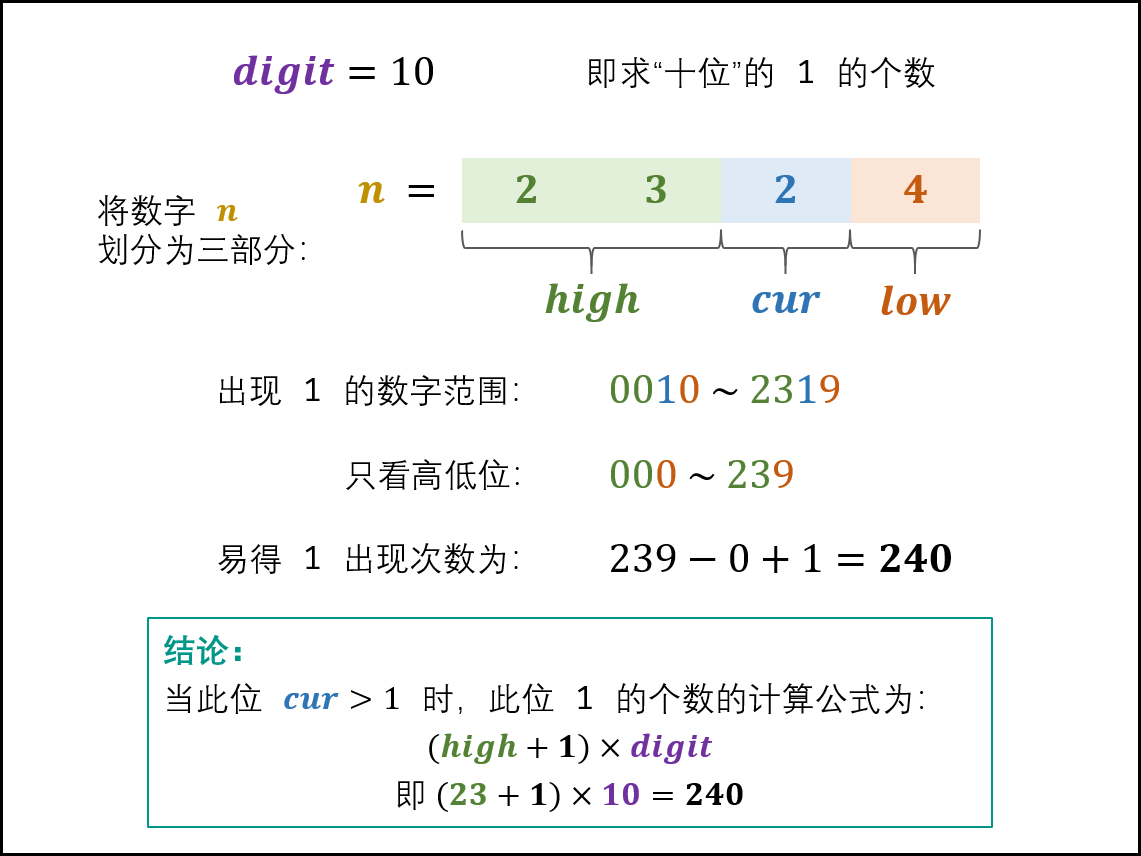
详细分析：
十位上1出现的次数怎么算呢？
此时与 cur=1 不同，cur=1 时出现的次数还需要看 low 的值，此时出现 1 的数字范围： 0010 ~ 2319 ，也就是说，高位为 23 时，低位也有 0 ~ 9 共计 10 种排列组合方法，与高位为 00 ~ 22 时一样，因此，cur=2~9 时，十位上 1 出现的次数为：24*10=240 。
上面各图源自jyd大佬
代码
class Solution {
public:int countDigitOne(int n) {long long digit = 1;int low = 0;int cur = n % 10;int high = n / 10;int sum = 0;while(high || cur){if(cur==0){sum += high * digit;}if(cur==1){sum += high*digit+low+1;}if(cur!=0 && cur!=1){sum += (high+1)*digit;}low += cur * digit;cur = high % 10;high /= 10;digit *= 10;}return sum;}
};
复杂度分析
时间复杂度 O(logn)： 循环内的计算操作使用 O(1) 时间；循环次数为数字 n 的位数，即 log10n，因此循环使用 O(logn) 时间。
空间复杂度 O(1) ： 几个变量使用常数大小的额外空间。
