Coursera自动驾驶课程第5讲：Vehicle Dynamic Modeling

在上一讲《Coursera自动驾驶课程第4讲：Safety Assurance for Autonomous Vehicles》中我们了解了自动驾驶汽车中一个非常重要的模块：安全模块。

本讲我们将学习新的模块：汽车运动学和动力学模块。（这部分可能需要一定的理论力学和汽车理论背景知识，没学过理论力学和汽车理论的话也不要紧，本部分模块难度也不是很大）。

B站视频链接：https://www.bilibili.com/video/BV1WE411D74g?p=1

文章目录

- - 1. Kinematic Modeling in 2D
  - - 1.1 Overview
    - 1.2 Coordinate frames and transformations
    - 1.3 Two-Wheeled Robot Kinematic Model
  - 2. The Kinematic Bicycle Model
  - - 2.1 Bicycle Kinematic Model
    - 2.2 State-space Representation
  - 3. Basic Dynamic Modeling in 2D
  - - 3.1 Overview
    - 3.2 Translational System
    - 3.3 Rotational Systems
    - 3.4 2D Dynamics
  - 4. Longitudinal Vehicle Model （重点）
  - - 4.1 Overview
    - 4.2 Resistance Force Models
    - 4.3 Powertrain Modeling
  - 5. Lateral Dynamic Bicycle Model （重点）
  - - 5.1 Lateral Dynamics of a Bicycle Model
    - 5.2 Space Representation of Lateral Model
  - 6. Vehicle Actuation
  - - 6.1 Steering Model
    - 6.2 Accelerating Model
    - 6.3 Braking Model
  - 7. Tire Slip & Modeling
  - - 7.1 Tire Slip
    - 7.2 Tire Modeling

1. Kinematic Modeling in 2D

1.1 Overview

在本模块中，我们将介绍自动驾驶汽车的运动学和动力学模块。在本模块中，将学习坐标系和运动学的基础知识，开发基于自行车模型的汽车运动学模型；探索汽车动力学模型的基础知识，开发纵向和侧向车辆动力学模式，创建用于转向，油门的执行器模型 ，最后研究轮胎滑移现象和轮胎模型。

在工程上，可以通过考虑定义其运动的几何约束或通过考虑作用在车辆上的所有力和力矩来对车辆运动建模。

第一种情况称为运动学建模。特别是在加速度不显着的低速行驶时，运动学建模足以捕获车辆的运动。
相反，当我们包括作用在车辆上的力和力矩的知识时，我们正在执行动力学建模。动力学模型可以很好地估计整个车辆运行范围内的车辆运动，但与运动学模型相比，动力学模型涉及更多的开发工作。

在这里插入图片描述

1.2 Coordinate frames and transformations

我们从2D转换开始介绍。按照惯例：

使用的坐标系是右手坐标系。
惯性坐标系是固定在地球上的固定参考系。通常，将此坐标系表示为相对于附近参考点的ENU坐标，或GNSS系统中使用的以地球为中心的ECEF坐标。
车辆坐标系，坐标原点一般为车辆的重心或后轴的中心点。
最后，是传感器坐标，用于描述传感器输出的坐标。

在自动驾驶汽车上一般会安装十几个传感器。为了使传感器数据表示一致，我们需要对坐标进行转换。

那么如何进行坐标转换呢？

（1）这里我们先看一个汽车速度向量的转换示例。通常，运动学变量（例如速度）以矢量的形式表示，具有大小和方向。在左边这幅图中，矢量 $v$ 使用绿色箭头表示。在这里有两个坐标系：

由轴 $b_1$ 和 $b_2$ 定义的载体坐标
由轴 $e_1$ 和 $e_2$ 定义的惯性坐标。

（2）假设两个坐标系具有相同的坐标原点。但是载体坐标 $b$ 相对于惯性坐标 $e$ 旋转了一定角度 $θ\theta$ 。然后，我们可以定义旋转矩阵 $C_{EB}$ ，表示将向量从载体坐标转换为惯性坐标，同样地，我们也可以定义旋转矩阵 $C_{BE}$ 。二者之间转换关系为：
$CEB=[cos⁡θsin⁡θ−sin⁡θcos⁡θ]，CBE=[cos⁡θ−sin⁡θsin⁡θcos⁡θ]C_{E B}=\left[\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta\end{array}\right]，C_{B E}=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta\end{array}\right]$

（3）在图3中，我们看到了一个两轮机器人，我们想表示机器人在载体坐标 $b$ 中观察到的点 $P$ 相对于惯性坐标 $e$ 的位置。机器人相对于惯性坐标的位置为 $x$ 和 $y$ ，机器人的方向夹角为 $θ\theta$ 。则二者坐标转换关系为：
$PB=CEB(θ)PE+OEB，PE=CBE(θ)PB+OBEP_{B}=C_{E B}(\theta) P_{E}+O_{E B}，P_{E}=C_{B E}(\theta) P_{B}+O_{B E}$

（4）最后，我们可以使用齐次坐标来总结两个坐标系之间的变换，坐标转换关系为：
$PE‾=[CEB(θ)∣OEB]PB‾\overline{P_{E}}=\left[C_{E B}(\theta) \quad \mid O_{E B}\right] \overline{P_{B}}$

1.3 Two-Wheeled Robot Kinematic Model

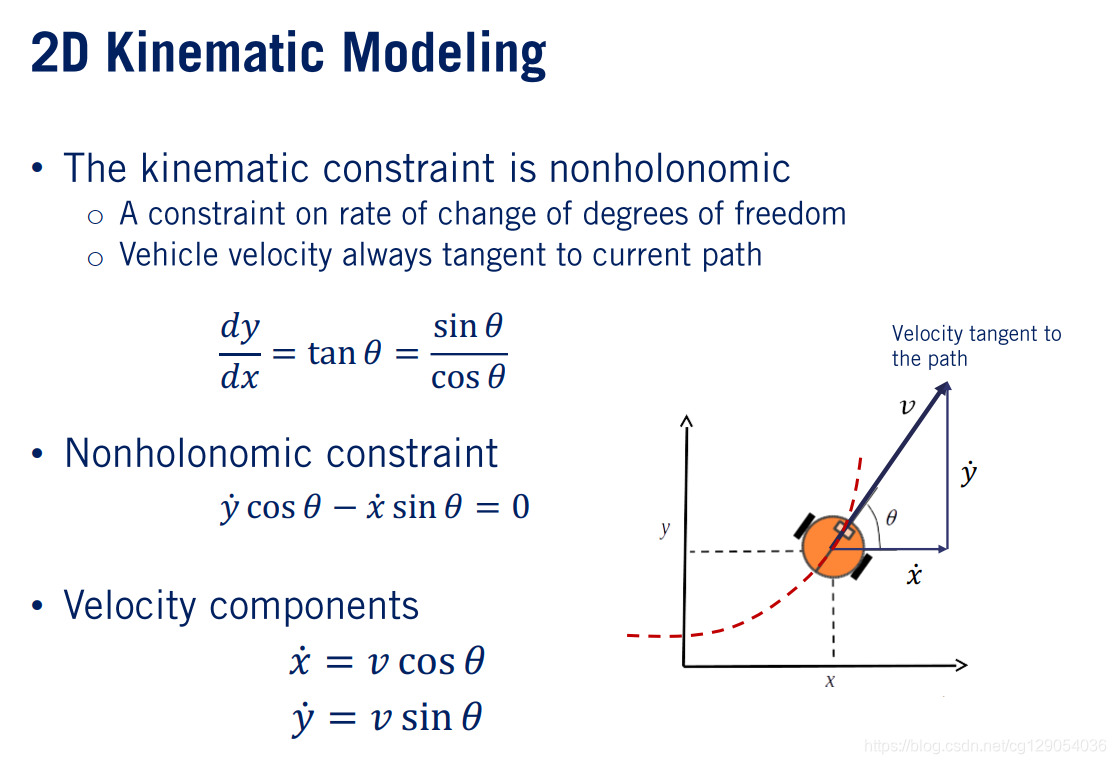
现在，我们准备开始对一个简单的机器人进行运动学建模。机器人的运动被限制为向前移动，车轮指向为运动方向。机器人的速度由其路径的切向量定义。让我们定义机器人运动方向的切向夹角 $θ\theta$ ，则有：
$dydx=tan⁡θ=sin⁡θcos⁡θ\frac{d y}{d x}=\tan \theta=\frac{\sin \theta}{\cos \theta}$
通过重新排列上面的方程，非完整约束方程的表达式如下：
$y˙cos⁡θ−x˙sin⁡θ=0\dot{y} \cos \theta-\dot{x} \sin \theta=0$
然后，我们可以通过组合这些方程来为机器人的运动构建一对方程，则运动方程为：
$x˙=vcos⁡θy˙=vsin⁡θ\dot{x}=v \cos \theta\\ \dot{y}=v \sin \theta$
现在，我们成功地为机器人建立了运动学模型。该模型以旋转速度的正向速度作为输入，并使用三个状态的矢量表示机器人。

回到我们的机器人，模型的输入是速度 $v$ 和方向变化率 $w$ 。但是，对于实际的两轮机器人，也可能需要直接命令轮速作为输入。现在，我们将研究如何扩展模型并将每个车轮的旋转速度与前进速度相关联。
（1）我们将需要定义一些其他变量，如下所示：

$P$ 是机器人的中心。
$L$ 是从机器人中心到每个轮子的距离。
$R$ 是轮子的半径。
$w_1$ 和 $w_2$ 是左右车轮的角速度。

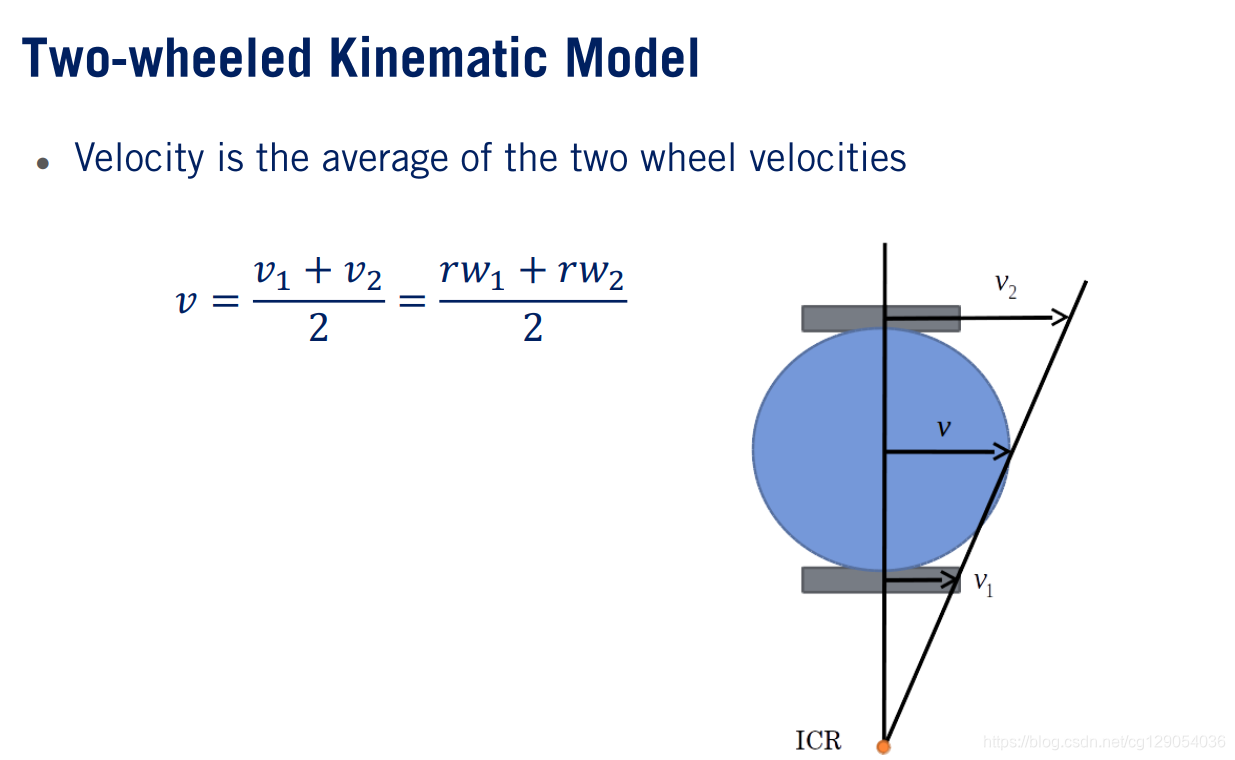
（2）机器人在每个车轮上的速度是车轮半径乘以其旋转速度。因此， $v_i=rw_{i}$ 。我们可以通过假设车轮和路面之间没有打滑来做到这一点。
（3）从该图可以看出，机器人的速度可以计算为两个车轮的平均速度。当两个车轮的速度相同时，机器人沿直线运动。
（4）如果车轮速度不同，则机器人将在某个瞬时旋转中心或ICR的弯曲路径上运动。

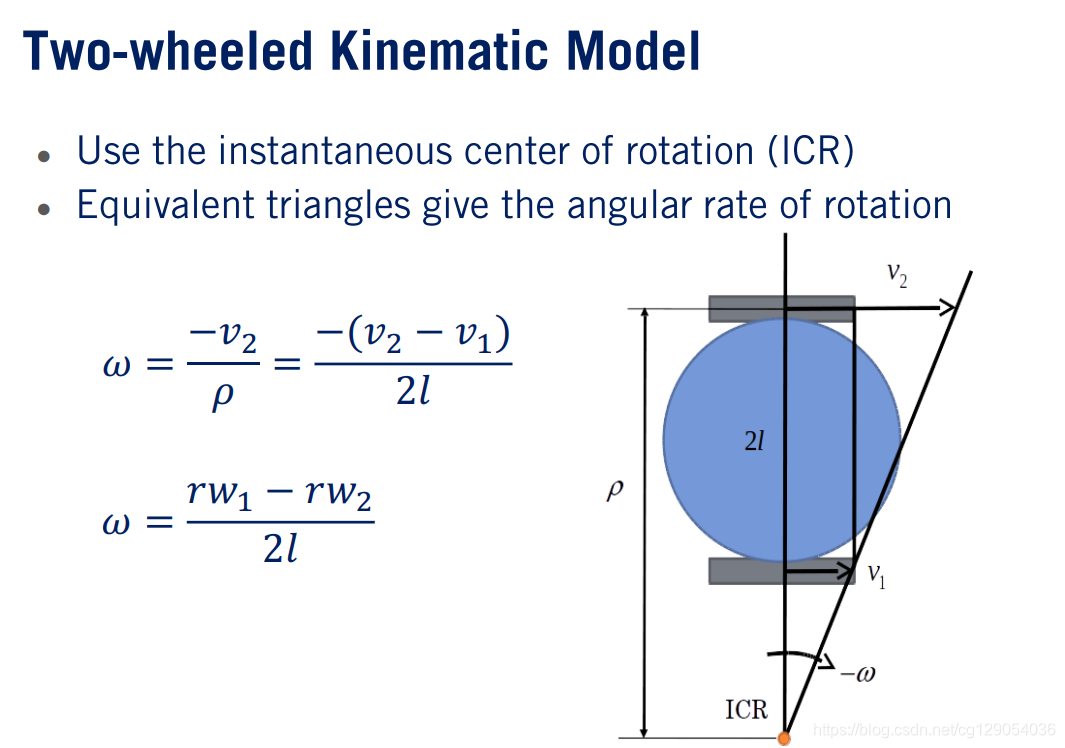现在，我们回到原始的机器人模型，并用新的表达式代替两轮机器人的速度和旋转速率。我们可以看到该模型的输入是 $w_1$ 和 $w_2$ ，它们是车轮的角速度。机器人的状态保持不变。同样，通过离散化连续时间方程，我们可以将模型从微分形式转换为有限差分形式。最终得到连续时间模型为：
$x˙=[(rw1+rw22)cos⁡θ]y˙=[(rw1+rw22)sin⁡θ]θ˙=(rw1−rw22l)\begin{aligned} \dot{x}&=\left[\left(\frac{r w_{1}+r w_{2}}{2}\right) \cos \theta\right] \\ \dot{y} &=\left[\left(\frac{r w_{1}+r w_{2}}{2}\right) \sin \theta\right] \\ \dot{\theta}&=\left(\frac{r w_{1}-r w_{2}}{2 l}\right) \end{aligned}$
离散时间模型为：
$xk+1=xk+[(rw1,k+rw2,k2)cos⁡θk]Δtyk+1=yk+[(rw1,k+rw2,k2)sin⁡θk]Δtθk+1=θk+(rw1,k−rw2,k2l)Δtx_{k+1}=x_{k}+\left[\left(\frac{r w_{1, k}+r w_{2, k}}{2}\right) \cos \theta_{k}\right] \Delta t\\ y_{k+1}=y_{k}+\left[\left(\frac{r w_{1, k}+r w_{2, k}}{2}\right) \sin \theta_{k}\right] \Delta t\\ \theta_{k+1}=\theta_{k}+\left(\frac{r w_{1, k}-r w_{2, k}}{2 l}\right) \Delta t$
在这里插入图片描述

2. The Kinematic Bicycle Model

2.1 Bicycle Kinematic Model

在本讲中，我们将研究自行车运动模型，这是一个非常经典的模型。

在推导模型之前，让我们先定义一些有关变量。我们将研究的自行车模型为前轮转向模型，我们平时所开的汽车一般都是前轮转向。我们假设车辆在由惯性坐标系 $F_{I}$ 表示的2维平面上运行。在提出的自行车模型中，前轮代表汽车的左右前轮，后轮代表汽车的左右后轮。要分析自行车模型的运动学，我们必须在车辆上选择一个参考点 $(X ， Y)$ ，该参考点可以选在后轴中心 $x_r,y_r)$ ，或前轴中心 $x_f,y_f)$ 或重心 $x_c,y_c)$ 。参考点的选择会影响所产生的运动方程，进而改变我们将要使用的控制器。

（1） Rear Axle Bicycle Model
我们从后轴参考点模型开始。

后轴参考点的位置表示为 $x_r，y_r)$ 。
自行车的前进方向夹角表示为 $θ\theta$ 。
$L$ 表示自行车的长度，以两个车轮轴线之间的长度为单位。
前轮的转向角用 $δ\delta$ 表示。
速度用 $v$ 表示。

由于没有考虑打滑情况，我们很容易得到车轮角速度与速度之间的关系：
$θ˙=ω=vR\dot{\theta}=\omega=\frac{v}{R}$
根据相似三角形，我们得到前轮转向角度 $δ\delta$ 为：
$tan⁡δ=LR\tan \delta=\frac{L}{R}$

联立上述两个方程，我们可以找到车辆的转速和前轮转角之间的关系：
$θ˙=ω=vR=vtan⁡δL\dot{\theta}=\omega=\frac{v}{R}=\frac{v \tan \delta}{L}$
我们可以为后轴参考点形成完整的运动自行车模型。基于此模型配置，参考点在 $x$ 和 $y$ 方向上的速度分量为：
$x˙r=vcos⁡θy˙r=vsin⁡θθ˙=vtan⁡δL\dot{x}_{r}=v \cos \theta\\ \dot{y}_{r}=v \sin \theta\\\dot{\theta}=\frac{v \tan \delta}{L}$

（2） Front Axle Bicycle Model & Gravity Bicycle Model
当以前轴的中心为参考点时，同理也可以构建自行车运动模型。速度关系为：
$x˙f=vcos⁡(θ+δ)y˙f=vsin⁡(θ+δ)θ˙=vsin⁡δL\dot{x}_{f}=v \cos (\theta+\delta)\\\dot{y}_{f}=v \sin (\theta+\delta)\\\dot{\theta}=\frac{v \sin \delta}{L}$

当选择重心或质心为参考点时。由于我们在前后轮上施加了无打滑约束，因此在重心处的运动方向与任一车轮的前进速度方向和自行车的前进方向都略有不同。最后，我们得出以下公式：
$x˙c=vcos⁡(θ+β)y˙c=vsin⁡(θ+β)θ˙=vcos⁡βtan⁡δLβ=tan⁡−1(lrtan⁡δL)\begin{aligned} \dot{x}_{c}& =v \cos (\theta+\beta) \\ \dot{y}_{c} &=v \sin (\theta+\beta) \\ \dot{\theta}& =\frac{v \cos \beta \tan \delta}{L} \\ \beta&=\tan ^{-1}\left(\frac{l_{r} \tan \delta}{L}\right) \end{aligned}$

2.2 State-space Representation

我们的运动学模型可以用四个状态表示： $\theta, \delta]^{T}$ 。

如果假设我们只能控制转向角 $ϕ\phi$ 的变化率，那么我们的自行车运动模型将速度 $v$ 和转向速度 $ϕ\phi$ 作为输入。最后我们得到如下关系：
$x˙c=vcos⁡(θ+β)y˙c=vsin⁡(θ+β)θ˙=vcos⁡βtan⁡δLδ˙=φ\dot{x}_{c} =v \cos (\theta+\beta) \\\dot{y}_{c}=v \sin (\theta+\beta) \\\dot{\theta}=\frac{v \cos \beta \tan \delta}{L} \\\dot{\delta}=\varphi$
在这里插入图片描述

3. Basic Dynamic Modeling in 2D

3.1 Overview

上一小节，我们研究了自行车运动模型。在本小节，我们将研究汽车动力学模型。

首先思考一个问题，为什么我们需要建立汽车动力学模型？当汽车以较高的速度行驶和转弯时，或者在道路打滑时，不打滑条件的假设不再成立。此外，汽车所受的牵引力和摩擦力需要额外的扭矩输入。

要构建典型的动力学模型，我们可以按照以下步骤进行。

首先，我们先确定在模型中使用的坐标系。例如，我们之前讨论过的车辆坐标和惯性坐标。
接下来，我们可以将系统拆分为一个个元素。在图中，有三个零件：弹簧，簧载质量和阻尼器。我们为每个元素定义一个力学模型。例如，弹簧作用力与位移成正比。阻尼器作用力与运动速度成比例
接下来，我们绘制元素列表中每个刚体的受力图。并正确命名作用在刚体上的所有力和力矩。
最后，通过使用牛顿第二定律，建立动力学模型数学方程。结果是一个描述我们刚体运动的常微分方程，这就是我们的动力学模型。

3.2 Translational System

下图中运动小车质量为 $M$ 。我们首先定义小车位置坐标系，坐标系用 $x$ 表示。然后我们确定刚体，在这种情况下，刚体是质量为 $M$ 的小车。接下来，我们绘制小车受力图并定义作用在推车上的所有力。在这种情况下，有三个力作用在推车上， $f_1$ 将推车向右拉， $f_2$ 和 $f_3$ 将推车向左拉。最后，我们在 $x$ 方向上应用牛顿第二定律来建立力学模型：
$\ddot{x}=f_{1}-f_{2}-f_{3}$

汽车减震器力学模型可采用相同的分析过程。受力分析如图所示，最终我们得到力学模型：
$\ddot{y}+b \dot{y}+k y=F$

3.3 Rotational Systems

现在让我们使用上述四步建模过程对车轮建立旋转动力学模型。

首先，我们建立坐标系。旋转方向上的一个坐标足以表示车轮的运动。我们将 $θ\theta$ 定义为车轮的角位置，将 $θ˙\dot{\theta}$ 点作为其旋转速度，将 $θ¨\ddot{\theta}$ 作为其角加速度。
接下来，轮胎模型由于旋转质量而具有旋转惯性 $J$ 。扭转刚度 $k$ 和阻尼 $b$ 由轮毂中轮胎的材料属性定义。我们通过来自车辆驱动轴的驱动扭矩来驱动车轮，并通过轮胎与路面相互作用产生的扭矩来阻止车轮前进。
现在，我们可以形成车轮系统的力学模型。驱动扭矩和负载扭矩之间的差定义了作用在车轮上的净扭矩。最终轮胎的旋转动力学方程为：
$\ddot{\theta}+b \dot{\theta}+k \theta=\tau_{\text {Drive}}-\tau_{\text {Load}}$

3.4 2D Dynamics

现在，我们可以将车辆动力学模型分为两个2D模型，将我们的车辆控制分为转向控制以及油门和制动控制问题。
(1) 纵向模型考虑了在倾斜道路上行驶的车辆。我们将车辆运动限制在 $X Z$ 平面上。有几种作用在车身和轮胎上的力，包括牵引力，滚动阻力，空气阻力和重力引力产生的坡度阻力。
(2) 同样，可以根据 $x y$ 平面中的运动来开发横向车辆动力学模型。从上向下查看车辆时。在此2D模型中，还存在一些作用在车辆上的侧向力，例如滑动力和离心力。

在下一课中，我们将介绍车辆的纵向动力学。并研究可调整驱动轮的传动系组件。会看到那里。

4. Longitudinal Vehicle Model （重点）

4.1 Overview

在本小节，我们将介绍车辆纵向动力学相关概念，以及在轮胎上产生扭矩所需的动力总成组件模型。

下图是在倾斜道路上，作用在车辆上前后轮胎力分别为 $F_{xf}$ 和 $F_{xr}$ 。空气阻力 $F_{aero}$ 和滚动阻力 $R_{xf}$ 和 $R_{xr}$ 。还有由于重力而产生的坡道分力 $mgsin⁡αmg\sin\alpha$ 。

根据牛顿第二定律，我们不难得出纵向上车辆的力学方程为：
$\ddot{x}=F_{x f}+F_{x r}-F_{a e r o}-R_{x f}-R_{x r}-m g \sin \alpha$
我们也可以对上述方程进行简化，简化后力学方程为：
$\ddot{x}=F_{x}-F_{a e r o}-R_{x}-m g \alpha$

4.2 Resistance Force Models

现在，让我们为汽车上的阻力建立一些简单的模型。
车辆的纵向运动受到空气阻力、滚动阻力和重力坡度分力的作用，坡度分力我们已经介绍过了。

这里我们进行空气动力学研究。通常空气阻力与空气密度，车辆迎风面积，风阻系数和车辆的速度有关。空气阻力数学形式为：
$Faero=1/2CaρAx˙2F_{\text {aero}}=1 / 2 C_{a} \rho A \dot{x}^{2}$

对于滚动阻力，我们也有一个类似的模型，该模型可以取决于法向力，轮胎压力和特性以及车速。这里我们给出线性关系：
$Rx=N(c^r,0+c^r,1∣x˙∣+c^r,2x˙2)≈(cr,1)∣x˙∣R_{x}=N\left(\hat{c}_{r, 0}+\hat{c}_{r, 1}|\dot{x}|+\hat{c}_{r, 2} \dot{x}^{2}\right) \approx\left(c_{r, 1}\right)|\dot{x}|$
在这里插入图片描述

4.3 Powertrain Modeling

为克服阻力而产生的力来自动力系统，由一系列组件产生。发动机或电池产生的机械能通常会经过传动系统进行扭矩放大传递给车轮。传动系是指发动机和车轮之间的组件顺序，通常包括离合器，变速器，差速器。（这一小节剩余内容可以查阅汽车构造和汽车理论书籍。）

5. Lateral Dynamic Bicycle Model （重点）

5.1 Lateral Dynamics of a Bicycle Model

在本小节，我们将介绍基于自行车建模方法的汽车侧向动力学模型。

（1）为了建立汽车侧向动力学模型，我们需要做几个假设：

首先，假设汽车向前的纵向车速恒定。这样做是为了解耦我们的侧向和纵向模型，这能够大大简化我们的建模任务，但是当汽车加速或减速出时确实会导致模型不准确。
其次，前后轴的左右车轮都集中在一个车轮中。因此，将四轮自行车模型转换为两轮自行车。
最后，假设其他非线性影响（如悬架运动，道路倾斜和空气阻力）可以忽略不计。

（2）侧向动力学方程

我们可以定义汽车总的侧向加速度为 $a_y$ ，其中包括汽车线性横向加速度 $y¨\ddot{y}$ ，以及来自车辆旋转向心加速度， $w^2R$ 。根据之前介绍过的内容，侧向动力学模型可以写为：
$V(\dot{\beta}+\dot{\psi})=F_{y f}+F_{y r}$

其中 $F_{yf}$ 和 $F_{yr}$ 时作用汽车前后轮的侧向力。同时，我们也能够得出力矩方程，其中 $l_f$ 和 $l_r$ 是汽车重心到前后轴的距离。
$Izψ¨=lfFyf−lrFyrI_{z} \ddot{\psi}=l_{f} F_{y f}-l_{r} F_{y r}$
在这里插入图片描述

（3）轮胎模型
现在我们开始探讨一些更常见的轮胎模型。一般在正常的行驶状态中，可以使用简单的线性近似来模拟轮胎力的产生。这种近似值实际上仅对较小的滑移角有效。为了使用这些线性轮胎模型，我们需要定义前后滑移角 $αf\alpha_f$ 和 $αr\alpha_r$ 。

轮胎的转弯刚度为其在车辆转弯时抵抗变形的能力。下图给出了轮胎侧向力与轮胎滑移角之间的关系。从图中可以看出，对于较小的滑移角，该关系几乎是线性关系。我们可以将 $C_f$ 和 $C_r$ 引入自行车模型的前后轮的线性转弯刚度。因此，作用在前轮和后轮上的侧向力之间的关系将是每个轮胎的转弯刚度 $C_y$ 和滑移角 $α$ 的乘积。

最终将=对以上所有公式进行整理，我们可以得到以下关于汽车质心侧偏角和横摆角关系（本节详细推导可以参考汽车理论横向稳定性一章）：
$β˙=−(Cr+Cf)mVβ+(Crlr−CflfmV2−1)ψ˙+CfmVδψ¨=Crlr−CflfIZβ−Crlr2+Cflf2IZVψ˙+CflfIZδ\dot{\beta}=\frac{-\left(C_{r}+C_{f}\right)}{m V} \beta+\left(\frac{C_{r} l_{r}-C_{f} l_{f}}{m V^{2}}-1\right) \dot{\psi}+\frac{C_{f}}{m V} \delta \\\ddot{\psi}=\frac{C_{r} l_{r}-C_{f} l_{f}}{I_{Z}} \beta-\frac{C_{r} l_{r}^{2}+C_{f} l_{f}^{2}}{I_{Z} V} \dot{\psi}+\frac{C_{f} l_{f}}{I_{Z}} \delta$

5.2 Space Representation of Lateral Model

现在我们可以定义一个侧向状态向量 $X_{lat}$ ， $Xlat=[yβψψ˙]TX_{\text {lat}}=\left[\begin{array}{llll}y & \beta & \psi & \dot{\psi}\end{array}\right]^{T}$
其中： $y$ 为汽车质心侧向位置， $β$ 为质心侧偏角， $ψ\psi$ 为横摆角；以及横摆角速率 $ψ˙\dot{\psi}$ 。

该系统现在可以用空间状态形式来表示：
$X˙lat=AlatXlat+Blatδ\dot{X}_{\text {lat}}=A_{\text {lat}} X_{\text {lat}}+B_{\text {lat}} \delta$
如果前进速度保持恒定，则系统动力学矩阵为 $A_{lat}$ 和 $B_{lat}$ ，它们是不变的。这里 $δ\delta$ 是驾驶员输入的转向角。
在这里插入图片描述

6. Vehicle Actuation

6.1 Steering Model

在本小节，我们将介绍关于车辆执行系统的基础知识，常见的执行操作有转向，加速和制动。

侧向力的来源是方向盘转角，纵向力的来源是油门踏板位置和制动踏板位置。车辆控制的主要任务是提供合适的转向节气门和制动命令，以使车辆保持在所需的路径上行驶。
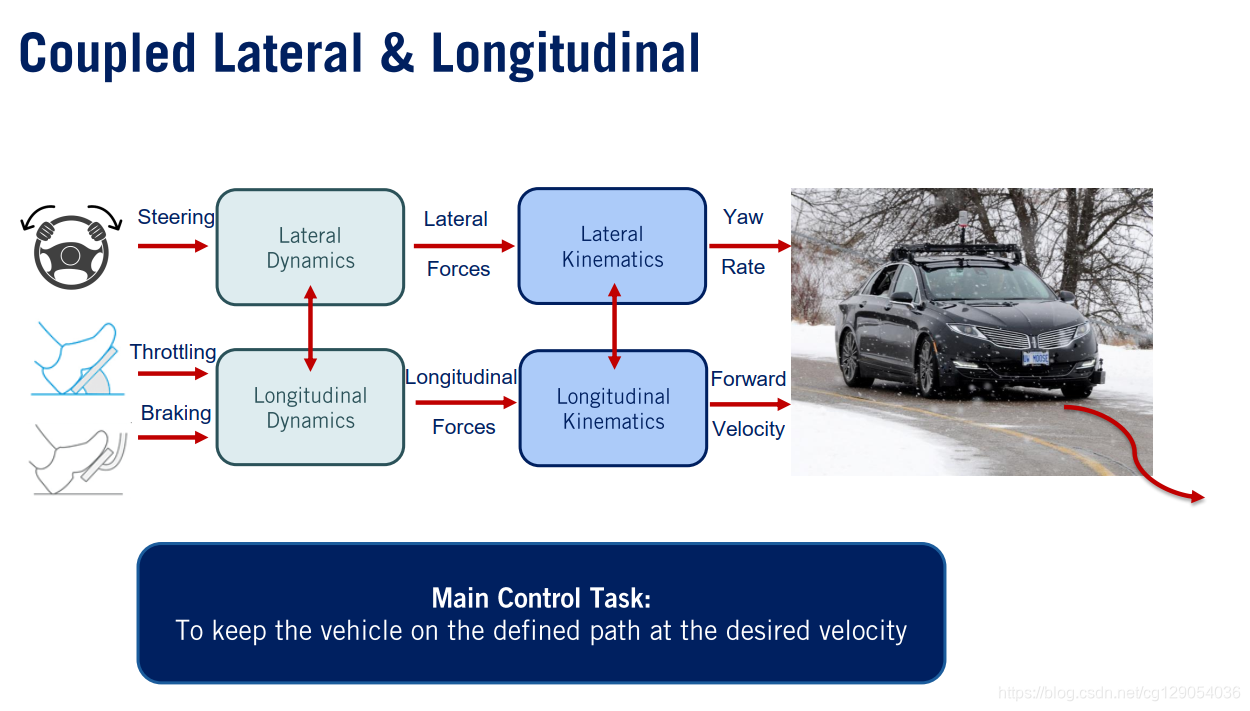
在这里插入图片描述
现在，让我们先看一下转向系统。转向系统控制车辆以使车辆向右或向左旋转。在转向系统的最简单模型中，车轮角度为与方向盘转角成比例。转向系统的主要作用是减速增扭。图中给出了转向系统的组成构件。

6.2 Accelerating Model

接下来是动力传动系统。

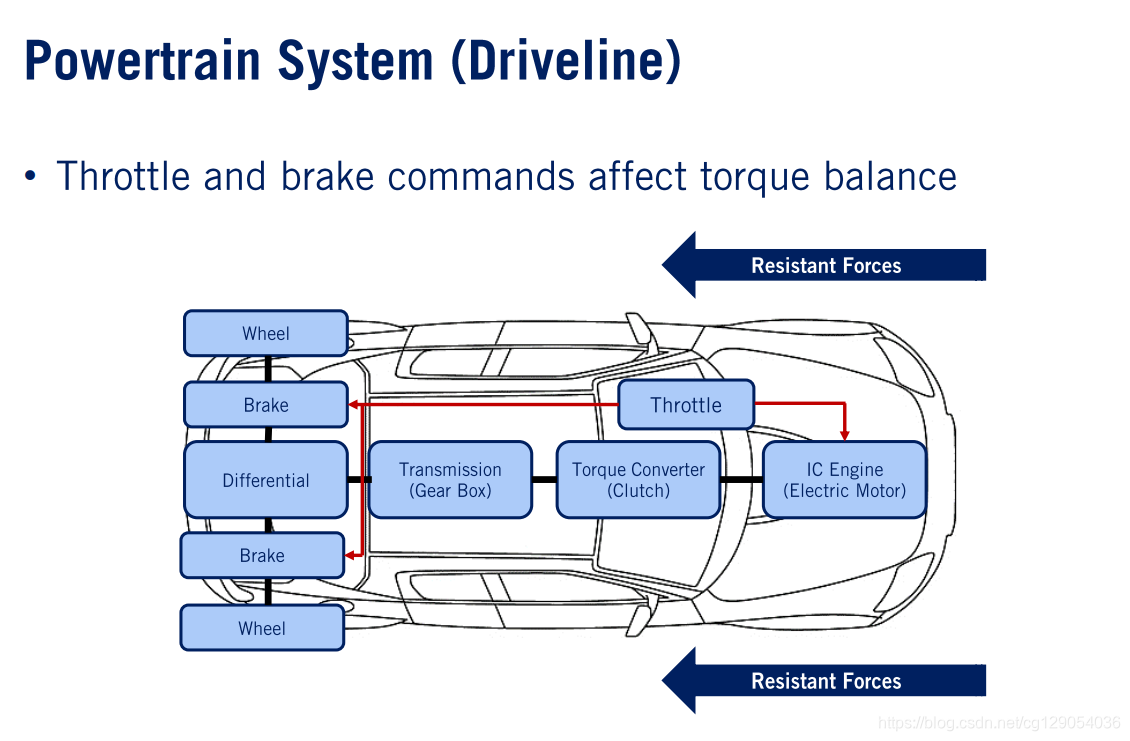
这里我们可以回顾一下功率流程图。功率流程图从诸如内燃机或电动机之类的动力源开始。脚踩油门踏板产生扭矩。该扭矩传递到传动系统。然后，基于工作模式和所需速度，切换变速器挡位。然后，动力通过差速器到车轮，并产生车轮扭矩，最终产生牵引力。牵引力必须大于阻力，阻力包括空气阻力和路面摩擦力，以使车辆在纵向方向上向前加速。

6.3 Braking Model

现在我们来讨论制动系统。制动过程从驾驶员踩下制动踏板位置开始，该位置通过电子控制单元转换为制动压力。制动压力在制动盘或制动鼓上产生制动力，该制动力成为车轮上的制动扭矩。车轮上的制动扭矩会产生负的纵向力，从而使车辆减速。

制动系统的一些主要功能包括：通过硬制动缩短制动距离；通过ABS在制动过程中保持汽车转向性；在制动过程中保持稳定性以避免侧翻。这些功能有助于扩大我们行驶安全操作条件范围，目前汽车制动功能已使车辆安全性和性能有了显着进步。

7. Tire Slip & Modeling

7.1 Tire Slip

在本小节，我们将探介绍侧偏角和滑移率的概念，并介绍一些经典的轮胎模型`。下面这幅图介绍了研究轮胎模型的重要性。施加在汽车上的作用力都是由轮胎产生的。
在这里插入图片描述

我们先介绍两个重要的概念：侧偏角和滑移率。

侧偏角是车辆前进方向与车辆实际运动方向之间的夹角，我们用 $β\beta$ 表示。数学公式为：
$β=tan⁡−1VyVx=tan⁡−1y˙x˙\beta=\tan ^{-1} \frac{V_{y}}{V_{x}}=\tan ^{-1} \frac{\dot{y}}{\dot{x}}$
为横向速度 $V_y$ 与纵向速度 $V_x$ 之比。

同样的，我们也可以定义每个轮胎的侧偏角。在此，前轮和后轮的轮胎侧偏角分别定义为 $αf\alpha_f$ 和 $αr\alpha_r$ 。轮胎侧偏角是轮胎前进的方向和车轮实际行驶的方向之间的角度。这里我们直接给出，轮胎前后侧偏角的数学公式：
$αr=−β+lrψ˙Vkαf=δ−β−lfψ˙V\alpha_{r}=-\beta+\frac{l_{r} \dot{\psi}}{V_{k}}\\\alpha_{f}=\delta-\beta-\frac{l_{f} \dot{\psi}}{V}$