本文介绍一篇 IMU 和 GPS 融合的惯性导航论文，重点是理解本文提出的：Dynamical constraints update、Roll and pitch updates 和 Position and heading updates。

论文链接为：https://www.sciencedirect.com/science/article/pii/S1665642314700963

---

1. Method Description

1.1 Vector state and system specification

首先系统状态量 $\hat{\mathrm{x}}$（22维） ：
$$\hat{\mathrm{x}}={\left[\begin{array}{lllllll}{q}^{nb}& {\omega }^b& {\mathrm{x}}_g& r^n& {\mathrm{v}}^n& a^n& {\mathrm{x}}_a\end{array}\right]}^{\prime }$$

其中：

• $q^{nb}=\left[{\mathrm{q}}_1,{\mathrm{q}}_2,{\mathrm{q}}_3,{\mathrm{q}}_4\right]$ 为单位四元数，表示导航坐标到载体坐标的坐标变换。
• ${\omega }^b=\left[{\omega }_{\mathrm{x}},{\omega }_{\mathrm{y}},{\omega }_{\mathrm{z}}\right]$ 是偏差补偿后的载体旋转角速度。
• ${\mathrm{x}}_g=\left[{\mathrm{x}}_{g\_\mathrm{x}},{}_{g\_\mathrm{y}},{\mathrm{x}}_{g\_\mathrm{z}}\right]$ 是角速度偏差。
• $r^n=\left[{\mathrm{x}}_{\mathrm{v}},{\mathrm{y}}_{\mathrm{v}},{\mathrm{z}}_{\mathrm{v}}\right]$ 是载体坐标原点在导航坐标下的位置。
• ${\mathrm{v}}^n=\left[{\mathrm{v}}_{\mathrm{x}},{\mathrm{v}}_{\mathrm{y}},{\mathrm{v}}_{\mathrm{z}}\right]$ 是载体在导航坐标下的速度。
• $a^n=\left[a_{\mathrm{x}},a_{\mathrm{y}},a_{\mathrm{z}}\right]$ 是载体在导航坐标下偏差补偿后的加速度。
• ${\mathrm{x}}_a=\left[{\mathrm{x}}_{a\_\mathrm{x}},{\mathrm{x}}_{a\_\mathrm{y}},{\mathrm{x}}_{a\_\mathrm{z}}\right]$ 是加速度偏差。

下图说明了载体坐标与导航坐标之间的关系，这里导航坐标为NED坐标。

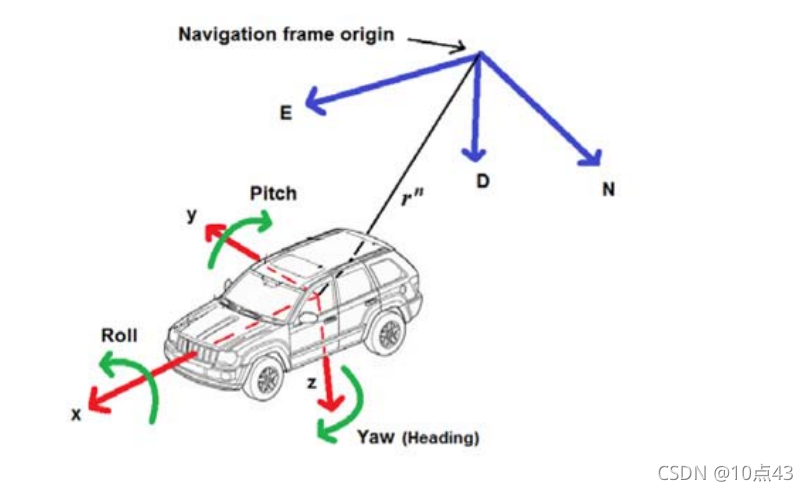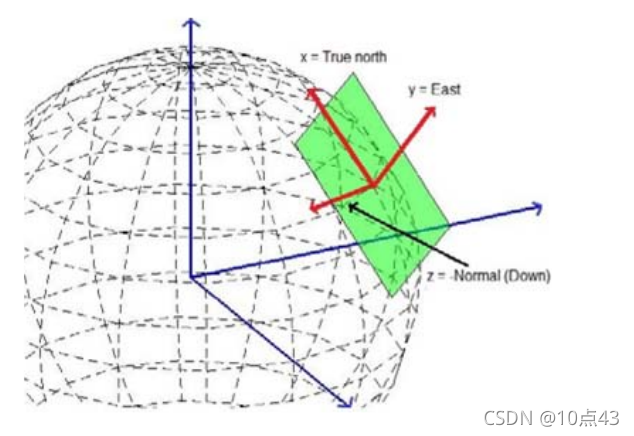在惯性导航系统中，需要考虑两种测量：

• 高频测量(IMU)。角速度测量模型为：${\mathrm{y}}_g={\omega }^b+{\mathrm{x}}_g+{\nu }_g$，其中 ${\mathrm{y}}_g$ 为测量值，${\mathrm{x}}_g$ 为角速度偏差，${\nu }_g$ 为角速度高斯白噪声，${\omega }^b$ 为角速度真值。加速度测量模型为：${\mathrm{y}}_a=a^b+g^b+{\mathrm{x}}_a+{\nu }_a$，其中 $g^b$ 为载体坐标下的重力向量，${\mathrm{x}}_a$ 是加速度偏差，${\nu }_a$ 是加速度高斯白噪声。
• 低频测量(GPS)。其位置 ${\mathrm{z}}_r$ 和 航向角 ${\mathrm{z}}_{\theta }$ 测量模型为：$\left[\begin{array}{c}{z}_r^n\\ z_{\theta }^n\end{array}\right]=\left[\begin{array}{c}{r}^n+{\nu }_r\\ {\theta }^n+{\nu }_{\theta }\end{array}\right]$。其中 $r^n$ 为导航位置，${\nu }_r$ 是位置高斯白噪声，${\theta }^n$ 是航向角，${\nu }_{\theta }$ 是航向角高斯白噪声。这里需要注意的是，处理时需要将GPS测量的WGS坐标转换成NED坐标。

---

1.2 Architecture of the system

系统结构如下图所示，包含预测和更新两部份。使用IMU数据进行预测，更新由三个子系统组成。

---

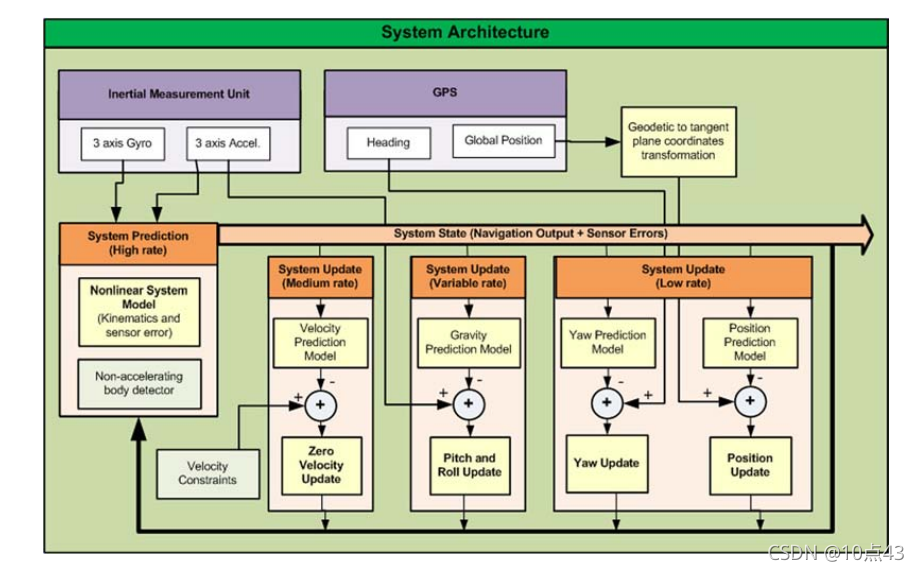
1.3 System prediction

当IMU数据到来时，系统进行预测，预测方程为：
$$\begin{array}{l}\text{ Attitude }\{\begin{array}{l}{q}_{(k+1)}^{nb}=q_{(k)}^{nb}\times q\left(R^{bn}{\left[{\omega }_{(k+1)}^b\Delta t\right]}^{\prime }\right)\\ {\omega }_{(k+1)}^b=-\left(y_{g(k)}-{\mathrm{x}}_{g(k)}\right)\\ {\mathrm{x}}_{\mathrm{g}(\mathrm{k}+1)}=\left(1-{\lambda }_{xg}\Delta t\right){\mathrm{x}}_{\mathrm{g}(\mathrm{k})}\end{array}\\ \text{ Position }\{\begin{array}{l}{r}_{(k+1)}^n=r_{(k)}^n+\left({\mathrm{v}}_{(k+1)}^n\Delta t\right)+\left(a_{(k+1)}^n\Delta t^2/2\right)\\ {\mathrm{v}}_{(k+1)}^n={\mathrm{v}}_{(k)}^n+\left(a_{(k+1)}^n\Delta t\right)\\ a_{(k+1)}^n=R^{bn}\left[y_{a(k)}-{\mathrm{x}}_{a(k)}\right]+g\\ {\mathrm{x}}_{a(k+1)}=\left(1-{\lambda }_{xa}\Delta t\right){\mathrm{x}}_{a(\mathrm{k})}\end{array}\end{array}$$

其中，${\lambda }_{\mathrm{x}\mathrm{g}},{\lambda }_{\mathrm{x}\mathrm{a}}$ 是加速度和角速度随时间变化的衰减系数，$\Delta t$ 是IMU采样时间，$g$ 是重力向量。

状态协方差 $P$ 更新方程为：
$$P_{(k+1)}=\nabla F_{\mathrm{x}}{P}_{(k)}\nabla F_{\mathrm{x}}^{\prime }+\nabla F_{\mathrm{u}}U\nabla F_{\mathrm{u}}^{\prime }$$

其中，矩阵 $U$ 为状态转移过程协方差矩阵，包含加速度和角速度噪声与偏差噪声，即 $U=\mathrm{diag}\left[\begin{array}{llll}{\sigma }_g{}^2{I}_{3\times 3}& {\sigma }_{xg}{}^2{I}_{3\times 3}& {\sigma }_a^2{I}_{3\times 3}& {\sigma }_{xa}{}^2{I}_{3\times 3}\end{array}\right]$

状态转移雅克比矩阵 $\nabla F_{\mathrm{x}}$ 和系统输入雅可比矩阵 $\nabla F_{\mathrm{u}}$ 为：
$$\nabla F_{\mathrm{x}}=\left[\begin{array}{ccccccc}\frac{\partial f{q}^{nb}}{\partial q^{nb}}& \frac{\partial f{q}^{nb}}{\partial {\omega }^b}& 0& 0& 0& 0& 0\\ 0& 0& \frac{\partial f{\omega }^b}{\partial {\mathrm{x}}_g}& 0& 0& 0& 0\\ 0& 0& \frac{\partial f{\mathrm{x}}_g}{\partial {\mathrm{x}}_g}& 0& 0& 0& 0\\ 0& 0& 0& \frac{\partial f{r}^n}{\partial r^n}& \frac{\partial f{r}^n}{\partial {\mathrm{v}}^n}& \frac{\partial f{r}^n}{\partial a^n}& 0\\ 0& 0& 0& 0& \frac{\partial f{\mathrm{v}}^n}{\partial {\mathrm{v}}^n}& \frac{\partial f{\mathrm{v}}^n}{\partial a^n}& 0\\ \frac{\partial f{a}^n}{\partial q^{nb}}& 0& 0& 0& 0& 0& \frac{\partial f{a}^n}{\partial {\mathrm{x}}_a}\\ 0& 0& 0& 0& 0& 0& \frac{\partial f{\mathrm{x}}_a}{\partial {\mathrm{x}}_a}\end{array}\right]$$

$$\nabla F_{\mathrm{u}}=\left[\begin{array}{cccc}0& 0& 0& 0\\ \frac{\partial f{\omega }^b}{\partial {\mathrm{y}}_g}& 0& 0& 0\\ 0& \frac{\partial f{\mathrm{x}}_g}{\partial {\nu }_{\mathrm{x}\mathrm{g}}}& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& \frac{\partial f{a}^n}{\partial {\mathrm{y}}_a}& 0\\ 0& 0& 0& \frac{\partial f{\mathrm{x}}_a}{\partial {\nu }_{\mathrm{x}\mathrm{a}}}\end{array}\right]$$

---

1.4 System update

EKF更新方程如下（作者这里写的形式可能有误）：
$$\begin{gathered} {\hat{\mathrm{x}}}_k={\hat{\mathrm{x}}}_{k+1}+W({\mathrm{z}}_i-h_i) \\ {P}_k=P_{k+1}-W{S}_i{W}^{\prime } \end{gathered}$$

其中，${\mathrm{z}}_i$ 是当前时刻测量值，$h_i=h(\hat{\mathrm{x}})$ 是预测测量，$W$ 是卡尔曼增益，计算方程为： $W=P_{k+1}\nabla H_i^{{}^{\prime }}{S}_i^{-1}$，$S_i$为：$S_i=\nabla H_i{P}_{k+1}\nabla H_i^{{}^{\prime }}+R_i$。其中，$\nabla H_i$ 是预测测量 $h(\hat{\mathrm{x}})$ 对系统状态量 $\hat{\mathrm{x}}$ 的测量雅可比矩阵，$R_i$ 是测量噪声协方差矩阵。根据以上方程可以发现，只要知道测量值、预测测量、测量雅克比矩阵、噪声即可进行状态更新。

1.4.1 Dynamical constraints update

首先是非完整性约束，如果 IMU的 $\mathrm{x}$ 轴和陆地汽车的 $\mathrm{x}$ 轴平行的话，则载体沿 $\mathrm{y}$ 和 $\mathrm{z}$ 轴的速度可以建模为：
$$\left[\begin{array}{c}{\mathrm{v}}_{\mathrm{y}}^b\\ {\mathrm{v}}_{\mathrm{z}}^b\end{array}\right]=\left[\begin{array}{c}0+{\nu }_{\mathrm{v}}\\ 0+{\nu }_{\mathrm{v}}\end{array}\right]$$

载体速度和导航速度关系为：
$${\left[\begin{array}{c}{\mathrm{v}}_{\mathrm{x}}^b,{\mathrm{v}}_{\mathrm{y}}^b,{\mathrm{v}}_{\mathrm{z}}^b\end{array}\right]}^{\prime }=\left[\begin{array}{c}{R}^{nb}{\mathrm{v}}^n\end{array}\right]$$

则现在已知测量值 ${\mathrm{z}}_i=[0,0{]}^{\prime }$，预测测量 $h_i=[{\mathrm{v}}_{\mathrm{y}}^b,{\mathrm{v}}_{\mathrm{z}}^b]$，噪声 $R={\mathbf{I}}_{2\times 2}{\sigma }_{\mathrm{v}}^2$，雅可比矩阵为 $\nabla H_i=\partial h_i/\partial \hat{\mathrm{x}}$，代入卡尔曼滤波，即可进行状态更新。

---

1.4.2 Roll and pitch updates

当载体加速度很小时($a^b\approx 0$)，则加速度模型可以写成：${\mathrm{y}}_a\approx g^b+{\nu }_a$ （忽略加速度偏差）。此时，加速度测量值为重力向量在载体坐标的分量，可以根据重力向量进行俯仰角修正。(不过在进行俯仰角修正时，需要使用零速检测算法进行静止判断)。

此时，重力向量测量值为：
$$h_g=R^{nb}[0,0,g_c{]}^{\prime }$$

其中，$g_c$ 为重力向量常数，现在已知测量值 ${\mathrm{z}}_i={\mathrm{y}}_a$，预测测量 $h_i=h_g$，噪声 $R={\mathbf{I}}_{3\times 3}{\sigma }_a^2$，雅可比矩阵为 $\nabla H_i=\partial h_g/\partial \hat{\mathrm{x}}$，代入卡尔曼滤波，即可进行状态更新。

---

1.4.3 Position and heading updates

位置更新，测量值 ${\mathrm{z}}_i={\mathrm{z}}_r^n$，预测测量 $h_i=h_r=[0_{3\times 10},{\mathrm{I}}_{3\times 3},0_{3\times 9}]\hat{\mathrm{x}}$，噪声 $R={\mathbf{I}}_{3\times 3}{\sigma }_r^2$，雅可比矩阵为 $\nabla H_i=[0_{3\times 10},{\mathrm{I}}_{3\times 3},0_{3\times 9}]$，代入卡尔曼滤波，即可进行状态更新。

航向角更新，测量值 ${\mathrm{z}}_i={\mathrm{z}}_{\theta }^n$，预测测量 $h_i=h_{\theta }=\mathrm{a}\mathrm{t}\mathrm{a}\mathrm{n}2(2({\mathrm{q}}_2{\mathrm{q}}_3-{\mathrm{q}}_1{\mathrm{q}}_4),1-2({\mathrm{q}}_3^2+{\mathrm{q}}_4^2))$，噪声 $R={\sigma }_{\theta }^2$，雅可比矩阵为$\nabla H_i=\partial h_{\theta }/\partial \hat{\mathrm{x}}$，代入卡尔曼滤波，即可进行状态更新。

---

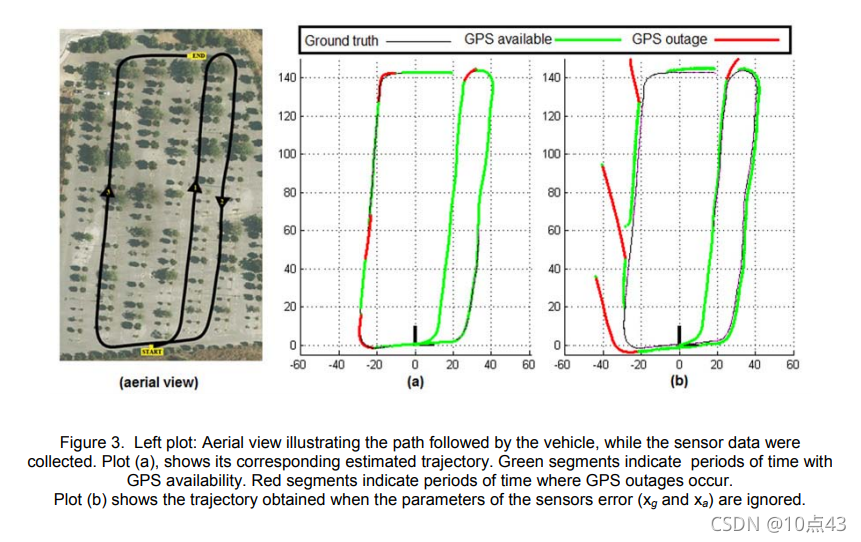
2. Experimental results

下面是实验参数设置和结果：
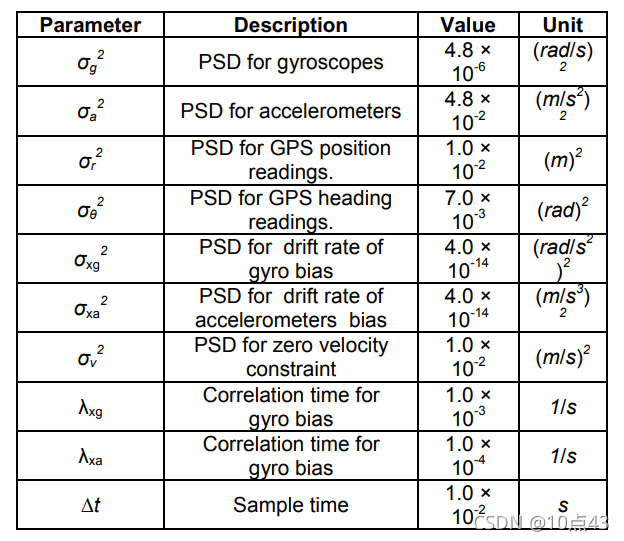