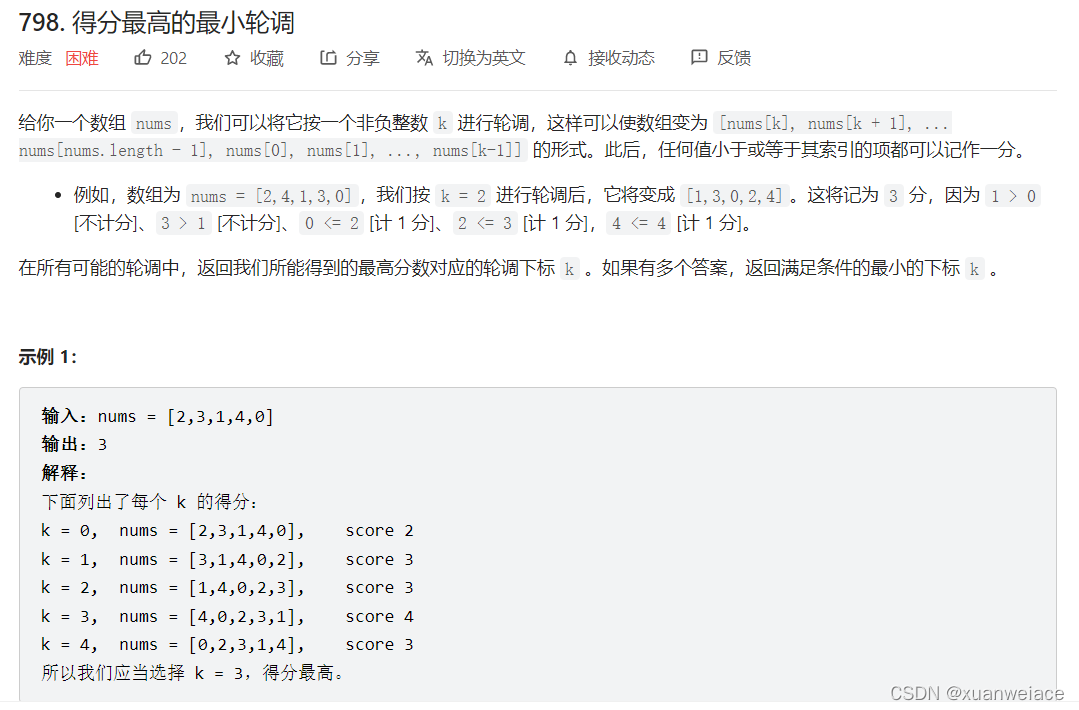
解题报告：

思路一：这题首先说一个nlogn的方法。

首先一个主客转化，题目描述是说把数组做翻转，idx不变，然后nums[i]和i作比较。那么我们可以转化为让数组不变，idx转变，即：假设刚开始i=4，那么idx的变化为[4,3,2,1,0,n-1,...,5]，再用nums[i] -  idx，如果这个值>0，则是符合区间的k。具体来说，比如

nums = [ 2, 3, 1, 4, 0]，对应的idx
idx  = [ 0, 1, 2, 3, 4]，作差后
diff = [-2,-2, 1,-1, 4]，此时k=0，然后移动一次的话，diff变为
diff = [ 2,-3, 0,-2, 3]，此时k=1，
diff = [ 1, 1,-1,-3, 2]，此时k=2，
diff = [ 0, 0, 3,-4, 1]，此时k=3，

即，不难发现，每次k变化的时候的时候，对应的就是全数组-1，然后在第k-1的位置上+n。

然后数组中>=0的元素个数就是k轮调的时候的答案。

因此我们需要，区间更新，单点更新吗，区间查询，这三个操作，可以用线段树维护，因而复杂度是nlogn。

思路二：

可以有两种方法过渡到思路二：

其一：刚刚的方法一直是在数组上做文章，即固定数组是不变的，然后变化k，来维护答案。那可否考虑直接从k上做文章，因为k最多就1e5，建立一个k的数组，我们直接考虑对于数组中的每个元素，会影响到哪些k值，做对应的更新。

其二：之前的想法是对于每一个k，遍历所有的元素找出对应答案。那么也可以对于每一个元素，考虑他会对哪些k产生影响，然后直接从k数组中维护，因此可以建立一个k数组。

综上，我们可以考虑每一个k，用类似数形结合的方法，可以方便的发现，当i<nums[i]时，k数组中只 有一段区间需要更新，当i>=nums[i]时，k数组中有两段区间需要更新。

这种思路还有一个好处就是，我们不需要动态更新和查询答案了。我们只需要记录每个元素对答案的影响，然后最后对答案数组查询一次就行了。

因此我们需要，区间更新，区间查询一次。因此我们不需要线段树了，可以用差分数组代替。

这种思路的转换还是很妙的，记录一下。

AC代码：（思路二的解法）

class Solution {
public:int num[200005];int bestRotation(vector<int>& nums) {int n = nums.size();for(int i = 0; i<n; i++) {if(i >= nums[i]) {int l = 0, r = i-nums[i];int ll = r + nums[i]+1, rr = n-1;num[l]++;  num[ll]++;num[r+1]--; num[rr+1]--;}else {int l = i+1, r = l1+(n-nums[i]-1);num[l]++;num[r+1]--;}}for(int i = 1; i<n; i++) {num[i] += num[i-1];}int ans = 0;for(int i = 0; i<n; i++) {if(num[i] > num[ans]) {ans = i;}}return ans;}
};