写在前面
题目收集来源自网络，前四题是开发岗的，后四题是算法岗的，因为代码无处提交，不一定正确，就不贴出来了，这里只写一下我的思路吧~欢迎大家一起讨论~~
1、
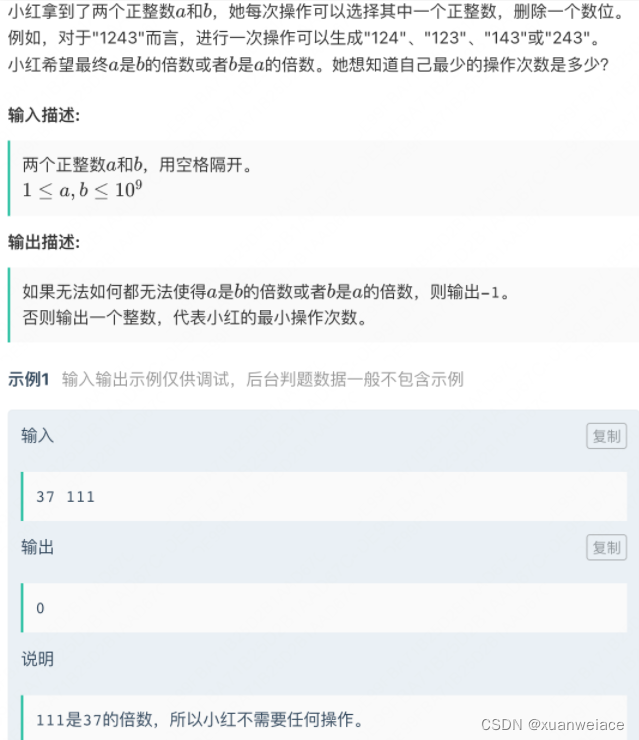
思路：因为最大1e9，也就是最多10位数字。且操作只跟结果有关，跟过程无关，因此可以对a和b分别二进制枚举删除的数字，这样a有2^10个可能性，b有2^10个可能性，然后暴力取操作次数的min就可以了。时间复杂度O(2^10^2)，正常写的话可能带个log，但是不难通过一些方法优化掉。
2、
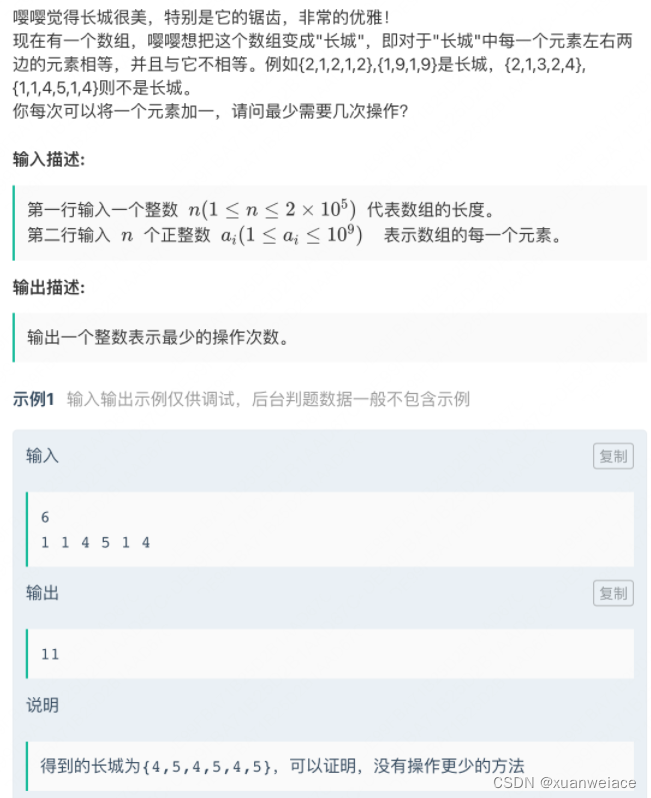
思路：分析题意不难发现，奇数位置一定是同一个数字，偶数位置一定是同一个数字，且操作只能+1，不能-1。所以分别加到奇数偶数分别的max就可以了。
3、
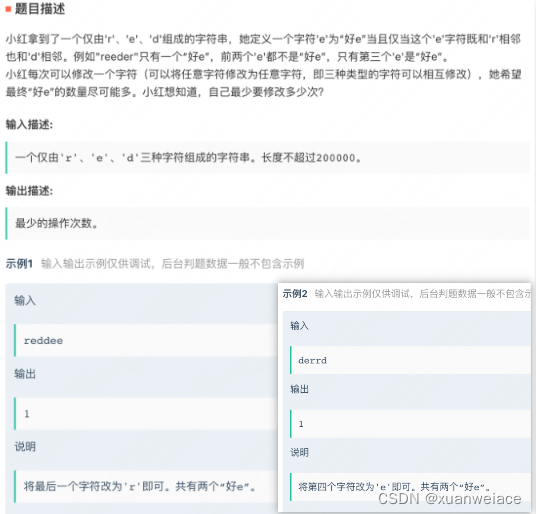
思路：读题发现，要求尽可能保证“好e”最大化，所以对于len(s)为奇数的情况，e只有一种摆法。对于len(s)为偶数的情况，e有两种摆法。
对于每一种摆法，又有r开头和d开头两种情况。然后分类讨论一下就好了。
4、
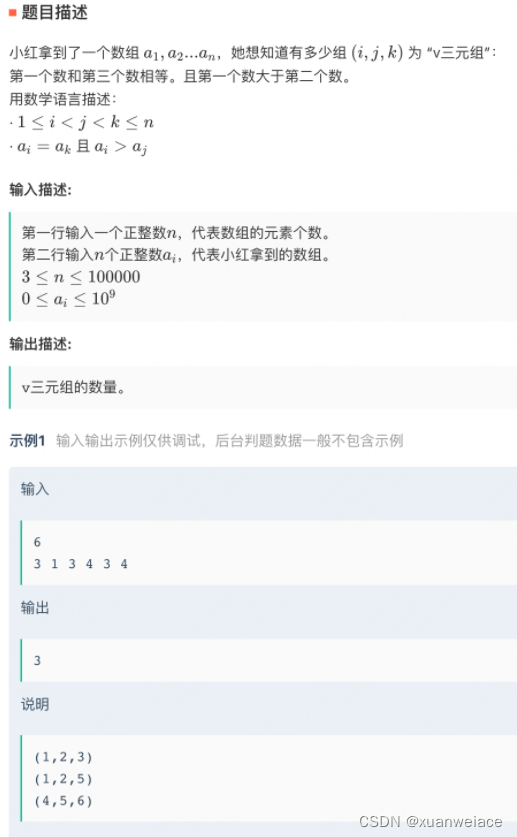
思路：从中间的元素入手，题意转化为：有多少三元组(a,b,a)，其中a>b。那么可以枚举每一个b，然后维护两个数组l和r，其中l[a]代表b左边有多少个值为a的元素，r[a]同理。然后树状数组维护l[a]*r[a]，当b移动的时候就动态计算并更新l，r，树状数组。统计的时候只需要统计树状数组后缀和就可以了。时间复杂度O(nlogn)，挺好的题。
5、
小红拿到一个数组，想在其中选择k个数使得这k个数的 按位与运算的值尽可能大。
输入，第一行n和k 用空格隔开
第二行 n个正整数ai，代表小红拿到的数组
思路：想了一个复杂度小于O(nlogn)的。首先排序，然后从高位向低位枚举，当第i位为1的个数>=k的时候，假设有n1个数，那就再从n1这些数里面遍历后续的低位。然后注意一些边界情况的处理，比如如果第i位为1的不够k个，或者刚好k个的情况。
网上找了一个代码，复杂度是O(30*n)的
n, k = map(int, input().split())
*nums, = map(int, input().split())cnt = [[0] * 30 for _ in range(n)]for i in range(n):tmp = nums[i]idx = -1while tmp:if tmp & 1:cnt[i][idx] += 1tmp = tmp >> 1idx -= 1
final = [0] * 30
exclude = set()
for i in range(30):tmp = 0s = set()for j in range(n):if j in exclude:continue if cnt[j][i] == 1:tmp += 1else:s.add(j)if tmp >= k:final[i] = 1 exclude = exclude | s print(int(''.join(map(str,final)), 2))6、（这题对于贪心的证明还是可以好好思考下的！！！）
一个长度为n的排列（比如[1,2,3]是一个排列，[1,2,5,3]则不是）每次可以让一个数字加一同时另一个数字减一，同时必须保证每次操作后依旧是一个排列。求：将这个排列变成非递减排列的最小操作次数？
n = int(input())
*nums, = map(int, input().split())hm = dict()
for i in range(n):hm[nums[i]] = i
res = []
acc = 0
for i in range(n):while nums[i] != i + 1:acc += 1idx2 = hm[nums[i] - 1]nums[i], nums[idx2] = nums[idx2], nums[i]hm[nums[idx2]] = idx2 hm[nums[i]] = i res.append([idx2, i])
print(acc)
for i in range(len(res)):print(res[i][0], res[i][1])贴一下wjh大佬的证明思路，为什么可以先考虑第一个数降为目标值，再考虑后续位置。
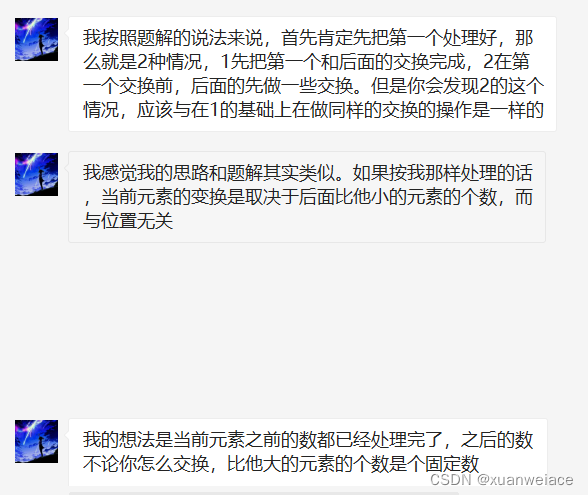
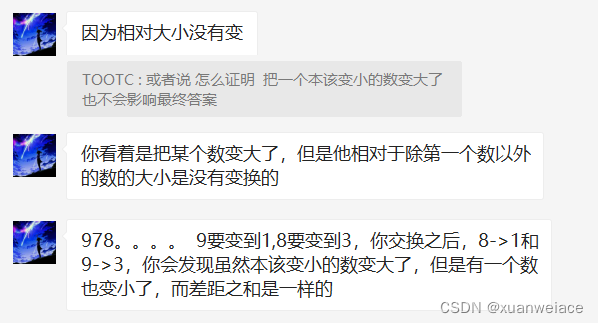
7、
小红拿到一个只包含 r e d三种字母的字符串，她想知道有多少子串满足 r e d三种字母的数量严格相等？
输入，一个仅包含red的字符串 长度不超过200000
s = input().strip()
from collections import defaultdict
hm = defaultdict(int)
hm['0,0,0'] = 1
r = e = d = 0
res = 0
for i in range(len(s)):if s[i] == 'r':r += 1if s[i] == 'e':e += 1if s[i] == 'd':d += 1state = f'{0},{e-r},{d-r}'res += hm[state]hm[state] += 1
print(res)思路：将差值存入一个map，相等问题转化为前缀问题，然后查map并维护即可。
8、输入三个数，a,b,n。前两个为前两个项的数，后面每个数都是前两个数的乘积的平方，输出第n个数，如果超了1e9+7要取余。n<=1e9
思路：分析会发现，数列为[a1b0, a0b1, a2b2, a4b6, a12b16]（数字代表次方），所以如果把a和b拆开来看的话，就会发现对于次方的通式为f[i]=2(f[i-1]+f[i-2])，配合矩阵快速幂就可求解。对于取余，可以用费马小定理（因为p是质数）
