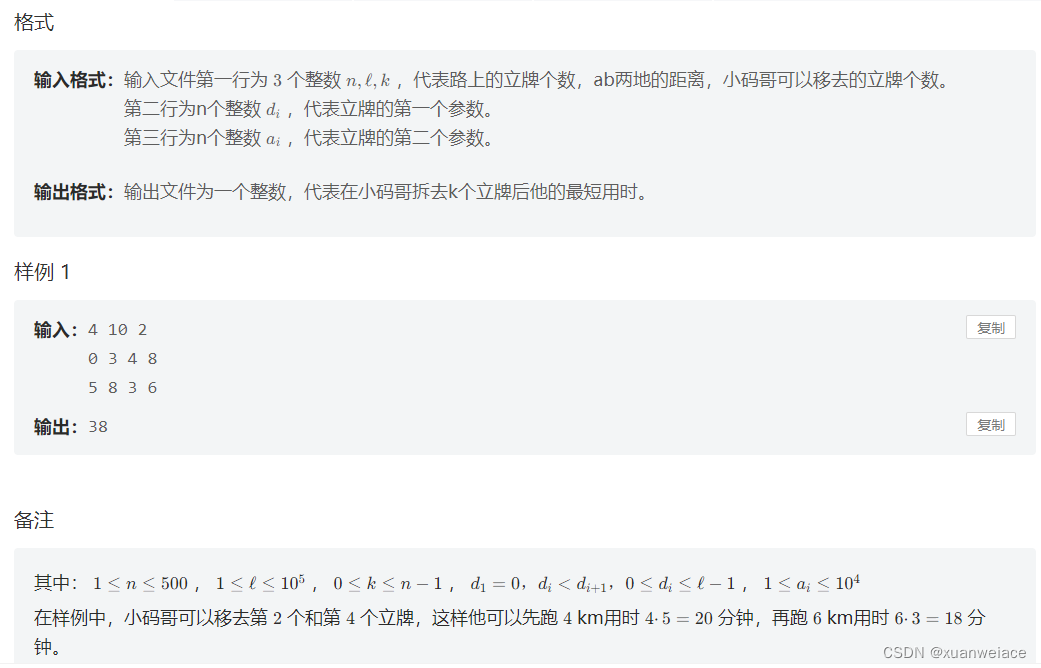
题目：
解题报告：
看数据范围，应该是个n^3的dp。
但是刚开始觉得二维就可以写。
但是G了，因为无法根据定义的状态判断从[i]到[i+1]的速度是多少。我这直接默认是d[i]了，但是显然不一定是。
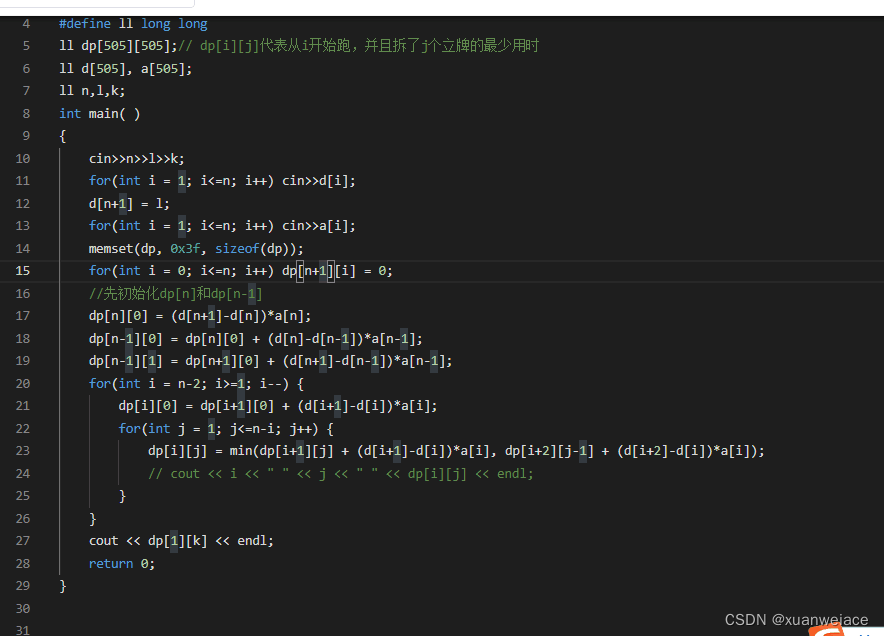
然后感觉欸，我是不是可以，还是【dp[i][j]代表跑到第i个，并且拆了j个牌子的最短时间】，这样定义状态，但是转移的时候再加一个遍历，从前面找到用时最少的转移过来，但是还是不对啊，局部最优解不代表全局最优解啊，这个速度不一定是全局最优解的速度啊
for(int i = 1; i<=n; i++) {dp[i][0] = dp[i-1][0] + (d[i]-d[i-1])*a[i];for(int j = 1; j<=k; j++) {dp[i][j] = dp[i-1][j] + (d[i]-d[i-1])*a[i];// 不拆for(int s = 1; s<=i-1; s++) {// 拆第s个dp[i][j] = min(dp[i][j], dp[s][j] + (d[i]-d[s])*a[s]);}}}其实我这个转移方程也不对，如果你想表示决策是：【把[s+1, i-1]都拆掉】，那还可以考虑这样的转移框架（dp[i]从dp[s]转移过来）。但是如果决策是【只考虑拆一个牌子】那肯定是用dp[i]从dp[i-1]转移的框架。
所以老老实实三维dp，dp[i][j][s]代表跑到第i个位置，拆了j个，并且到位置i时的速度是a[s]，的最小时间花费。时间复杂度O(n^3)，空间复杂度O(n^3)
然后代码如下：
#include<bits/stdc++.h> using namespace std;
#define ll long long
ll dp[2][505][505];// dp[i][j][s]代表跑到i个立牌，并且拆了j个立牌，最后速度是a[s]的最少用时ll d[505], a[505];
ll n,l,k;
const ll INF = 1e16;
int main( )
{cin>>n>>l>>k;for(int i = 1; i<=n; i++) cin>>d[i];d[n+1] = l;for(int i = 1; i<=n; i++) cin>>a[i];memset(dp, 0x3f, sizeof(dp));//第2个柱子dp[0][0][1] = (d[2]-d[1])*a[1];// dp[i][j][s] 跑到第i个，拆了j个，以s的速度跑的。//如何确定自己dp设定状态是带有冗余状态的。for(int i = 3; i<=n+1; i++) {memset(dp[idx], 0x3f, sizeof(dp[idx]));for(int j = 0; j<=k; j++) {// 不删第i-1个 ,只有这种情况第三维才是i-1，其他情况第三维都<i-1ll mx = INF;for(int s = 0; s<=i-2; s++) mx = min(mx, dp[i-1][j][s]);dp[i][j][i-1] = mx + (d[i]-d[i-1])*a[i-1];// 以第i-1的速度if(j == 0) continue;//必删第i-1个for(int s = 0; s<i-1; s++) {// 以第s个的速度过来dp[i][j][s] = dp[i-1][j-1][s] + (d[i]-d[i-1])*a[s];// 以第[0,i-2]速度// dp[i][j][s] = dp[s][j-1][s] + (d[i]-d[s])*a[s]; 注意这里不能是s，第一维都必须是i-1}}}ll ans = INF;for(int i = 0; i<=n; i++) {ans = min(ans, dp[(n+1)%2][k][i]);}cout << ans << endl;return 0;
}
然后发现数组开不了这么大，滚动优化一下：时间复杂度O(n^3)，空间复杂度O(n^2)
AC代码：
#include<bits/stdc++.h> using namespace std;
#define ll long long
ll dp[2][505][505];// dp[i][j]代表从i开始跑，并且拆了j个立牌的最少用时ll d[505], a[505];
ll n,l,k;
const ll INF = 1e16;
int main( )
{cin>>n>>l>>k;for(int i = 1; i<=n; i++) cin>>d[i];d[n+1] = l;for(int i = 1; i<=n; i++) cin>>a[i];memset(dp, 0x3f, sizeof(dp));//第2个柱子dp[0][0][1] = (d[2]-d[1])*a[1];// printf("dp[%d][%d][%d]=%lld\n", 2,0,1, dp[0][0][1]);// dp[i][j][s] 跑到第i个，拆了j个，以s的速度跑的。//如何确定自己dp设定状态是带有冗余状态的。for(int i = 3; i<=n+1; i++) {int idx = i%2;int idx2 = 1-idx;memset(dp[idx], 0x3f, sizeof(dp[idx]));for(int j = 0; j<=k; j++) {// 不删第i-1个 ,只有这种情况第三维才是i-1，其他情况第三维都<i-1ll mx = INF;for(int s = 0; s<=i-2; s++) mx = min(mx, dp[idx2][j][s]);dp[idx][j][i-1] = mx + (d[i]-d[i-1])*a[i-1];// 以第i-1的速度// printf("dp[%d][%d][%d]=%lld\n", i,j,i-1, dp[idx][j][i-1]);if(j == 0) continue;//必删第i-1个for(int s = 0; s<i-1; s++) {// 以第s个的速度过来dp[idx][j][s] = dp[idx2][j-1][s] + (d[i]-d[i-1])*a[s];// 以第[0,i-2]速度// printf("dp[%d][%d][%d]=%lld\n", i,j,s, dp[idx][j][s]);}}}ll ans = INF;for(int i = 0; i<=n; i++) {ans = min(ans, dp[(n+1)%2][k][i]);}cout << ans << endl;return 0;
}总结：
注意这题的几个细节点：
1、因为最后一个立牌不是终点，所以需要把终点当做第n+1个立牌。这样dp直接到n+1
2、注意这题初始化需要初始化dp[1]和dp[2]，然后从3开始递推。
