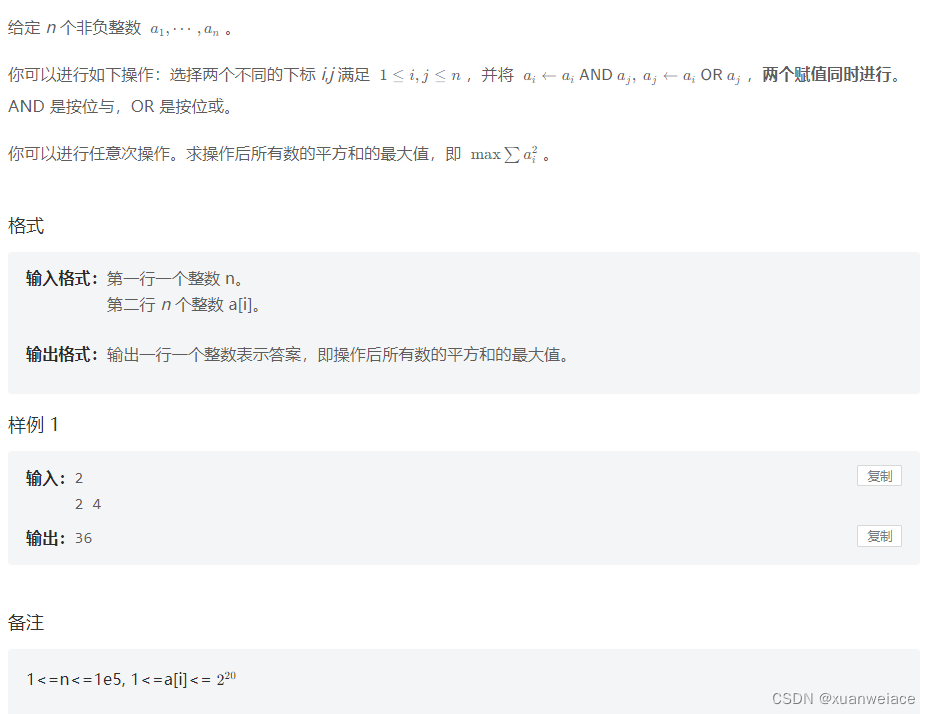
题目：

解题报告：

首先预备几个结论：

1、对于两个数a,b ，生成a&b和a|b，则一定对应一个常数c，使得生成的两个数分别是a+c和a-c。

2、对于两个数a,b，生成a&b和a|b的前后，二进制的1的个数是不变的。

基于以上两点（对于这一题，主要是第二点），我们可以简单的进行扩展这个结论，对于任意出现过的某个数位的1，都可以进行任意的排列组合。思路就是直接贪心，打散后按照贪心策略重组出最后结果，即可以生成任意一个序列，只要他们和初始序列的二进制的1的个数是一样的。

因为我们发现，对于平方和，数字集中在越少的个数上，值越大，比如(4+1)^2>4^2+1^2，以此类推，所以贪心的策略显而易见。（没有证明，猜的一个结论）

AC代码：

#include<bits/stdc++.h> using namespace std;
int cnt[55];
int n, mx;
int main( )
{cin>>n;for(int x, i = 1; i<=n; i++) {cin>>x;int p = 0;while(x) {if(x%2 == 1) cnt[p] ++;x /= 2;p ++;}mx = max(mx, p);}long long ans = 0;for(int i = 0; i<n; i++) {long long t = 0;for(int j = 0; j<mx; j++) {if(cnt[j] > 0) t += (1<<j), cnt[j]--;}ans += t * t;}cout << ans;return 0;
}