冒泡、插入、选择 O(n²) 基于比较

快排、归并 O(nlogn) 基于比较
计数、基数、桶 O(n) 不基于比较

一、如何分析一个排序算法？

1. 学习排序算法的思路？明确原理、掌握实现以及分析性能。
2. 如何分析排序算法性能？从执行效率、内存消耗以及稳定性3个方面分析排序算法的性能。
3. 执行效率：从以下3个方面来衡量
   1）最好情况、最坏情况、平均情况时间复杂度
   2）时间复杂度的系数、常数、低阶：排序的数据量比较小时考虑
   3）比较次数和交换（或移动）次数
4. 内存消耗：通过空间复杂度来衡量。针对排序算法的空间复杂度，引入原地排序的概念，原地排序算法就是指空间复杂度为O(1)的排序算法。
5. 稳定性：如果待排序的序列中存在值等的元素，经过排序之后，相等元素之间原有的先后顺序不变，就说明这个排序算法时稳定的。

二、冒泡排序

1.排序原理

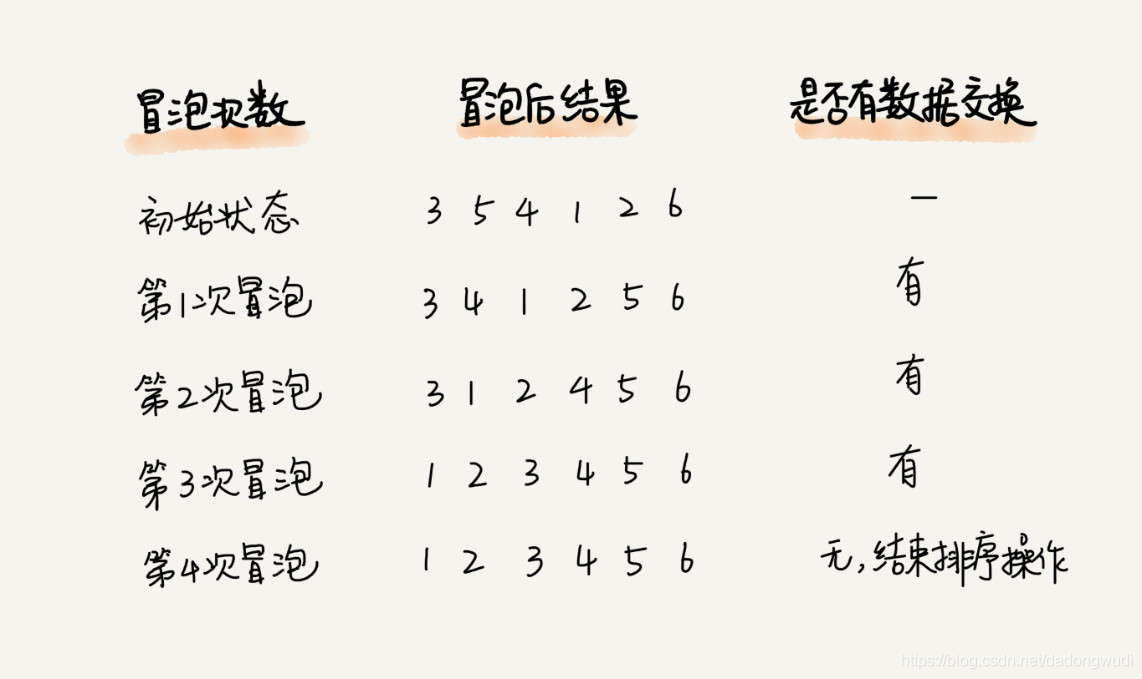
1）冒泡排序只会操作相邻的两个数据。
2）对相邻两个数据进行比较，看是否满足大小关系要求，若不满足让它俩互换。
3）一次冒泡会让至少一个元素移动到它应该在的位置，重复n次，就完成了n个数据的排序工作。
4）优化：若某次冒泡不存在数据交换，则说明已经达到完全有序，所以终止冒泡。

2.代码实现

// 冒泡排序，a表示数组，n表示数组大小
public void bubbleSort(int[] a, int n) {if (n <= 1) return;for (int i = 0; i < n; ++i) {// 提前退出冒泡循环的标志位boolean flag = false;for (int j = 0; j < n - i - 1; ++j) {if (a[j] > a[j+1]) { // 交换int tmp = a[j];a[j] = a[j+1];a[j+1] = tmp;flag = true;  // 表示有数据交换      }}if (!flag) break;  // 没有数据交换，提前退出}
}

3.性能分析

1）执行效率：最小时间复杂度、最大时间复杂度、平均时间复杂度
最小时间复杂度：数据完全有序时，只需进行一次冒泡操作即可，时间复杂度是O(n)。
最大时间复杂度：数据倒序排序时，需要n次冒泡操作，时间复杂度是O(n^2)。
平均时间复杂度：通过有序度和逆序度来分析。
对于包含n个数据的数组进行冒泡排序，平均交换次数是多少呢？最坏的情况初始有序度为0，所以要进行n*(n-1)/2交换。最好情况下，初始状态有序度是n*(n-1)/2，就不需要进行交互。我们可以取个中间值n*(n-1)/4，来表示初始有序度既不是很高也不是很低的平均情况。
换句话说，平均情况下，需要n*(n-1)/4次交换操作，比较操作可定比交换操作多，而复杂度的上限是O(n²)，所以平均情况时间复杂度就是O(n²)。
2）空间复杂度：每次交换仅需1个临时变量，故空间复杂度为O(1)，是原地排序算法。
3）算法稳定性：如果两个值相等，就不会交换位置，故是稳定排序算法。

三、 插入排序（Insertion Sort）

1.算法原理

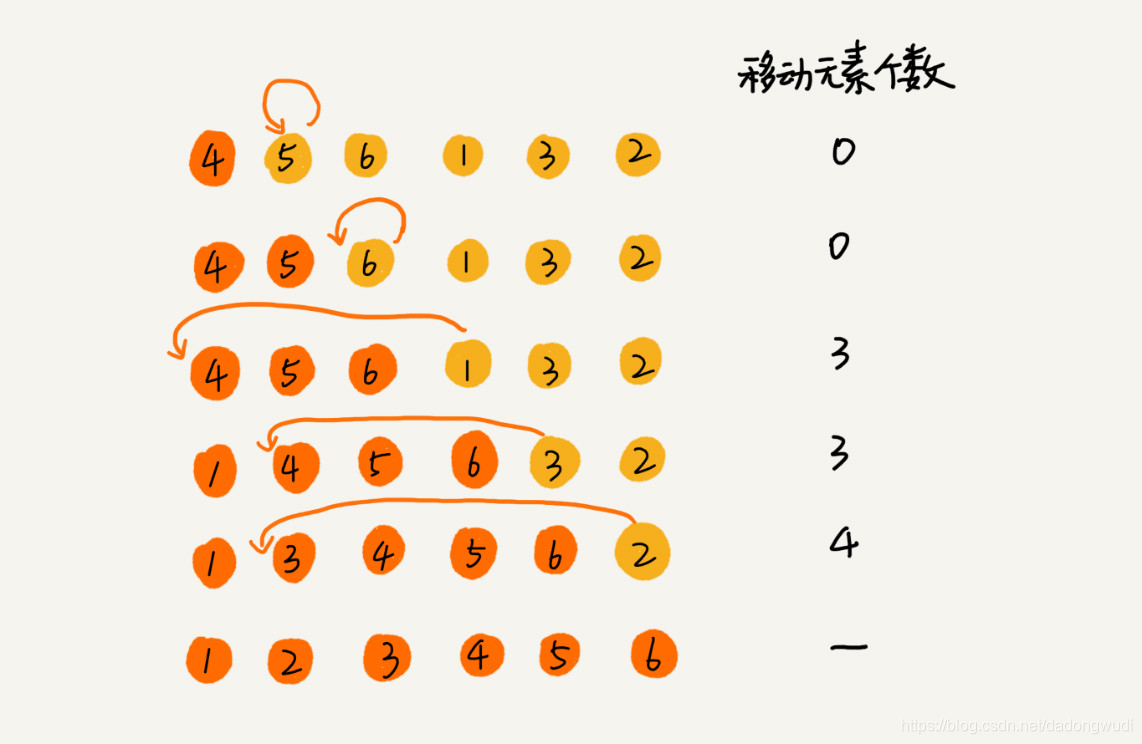
首先，我们将数组中的数据分为2个区间，即已排序区间和未排序区间。初始已排序区间只有一个元素，就是数组的第一个元素。插入算法的核心思想就是取未排序区间中的元素，在已排序区间中找到合适的插入位置将其插入，并保证已排序区间中的元素一直有序。重复这个过程，直到未排序中元素为空，算法结束。

2.代码实现

// 插入排序，a表示数组，n表示数组大小
public void insertionSort(int[] a, int n) {if (n <= 1) return;for (int i = 1; i < n; ++i) {int value = a[i];int j = i - 1;// 查找插入的位置for (; j >= 0; --j) {if (a[j] > value) {a[j+1] = a[j];  // 数据移动} else {break;}}a[j+1] = value; // 插入数据}
}

3.性能分析

1）时间复杂度：最好、最坏、平均情况
如果要排序的数组已经是有序的，我们并不需要搬移任何数据。只需要遍历一遍数组即可，所以时间复杂度是O(n)。如果数组是倒序的，每次插入都相当于在数组的第一个位置插入新的数据，所以需要移动大量的数据，因此时间复杂度是O(n²)。而在一个数组中插入一个元素的平均时间复杂都是O(n)，插入排序需要n次插入，所以平均时间复杂度是O(n²)。
2）空间复杂度：从上面的代码可以看出，插入排序算法的运行并不需要额外的存储空间，所以空间复杂度是O(1)，是原地排序算法。
3）算法稳定性：在插入排序中，对于值相同的元素，我们可以选择将后面出现的元素，插入到前面出现的元素的后面，这样就保持原有的顺序不变，所以是稳定的。

四、选择排序（Selection Sort）

1.算法原理

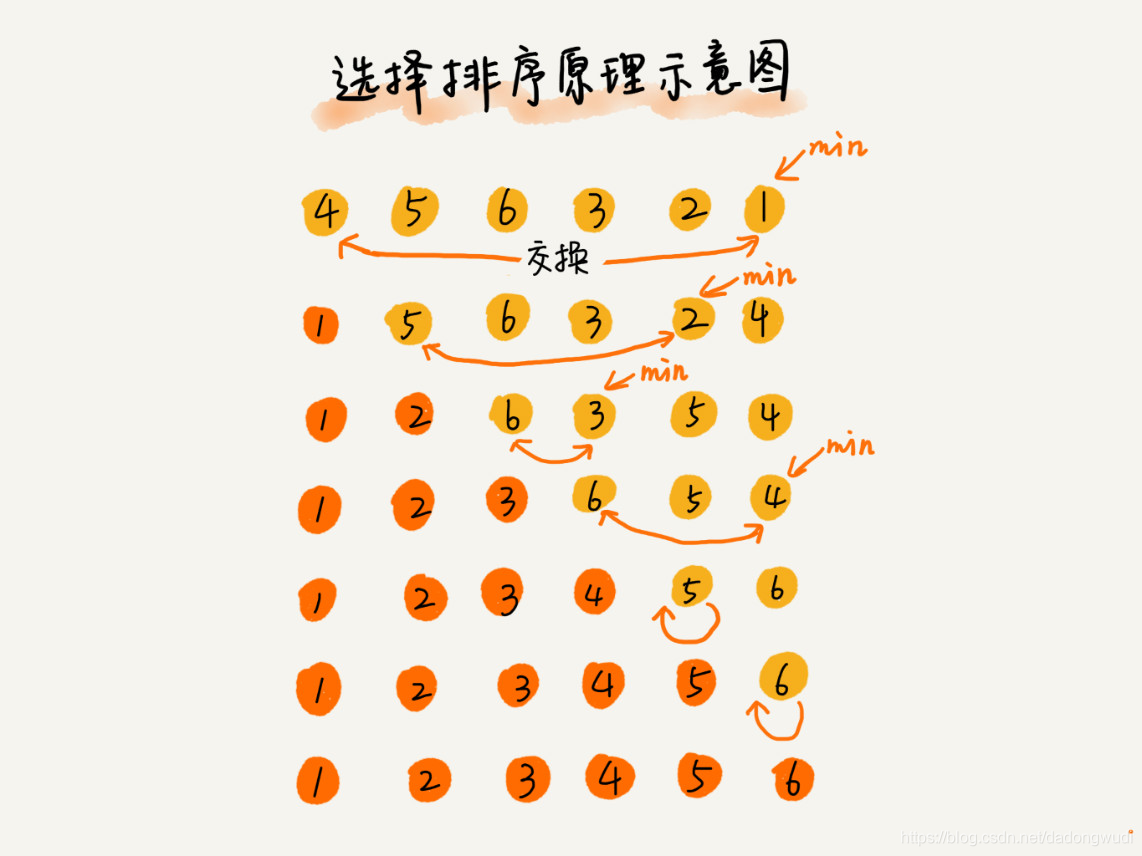
选择排序算法也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素，并将其放置到已排序区间的末尾。

2.代码实现

/*** 选择排序* @param a 待排序数组* @param n 数组长度*/
public static void selectSort(int[] a, int n) {
if(n<=0) return;for(int i=0;i<n;i++){int min=i;for(int j=i;j<n;j++){if(a[j] < a[min]) min=j;}if(min != i){int temp=a[i];a[i]=a[min];a[min]=temp;}}
}

3.性能分析

1）时间复杂度：最好、最坏、平均情况
选择排序的最好、最坏、平均情况时间复杂度都是O(n²)。为什么？因为无论是否有序，每个循环都会完整执行，没得商量。
2）空间复杂度：
选择排序算法空间复杂度是O(1)，是一种原地排序算法。
3）算法稳定性：
选择排序算法不是一种稳定排序算法，比如[5,8,5,2,9]这个数组，使用选择排序算法第一次找到的最小元素就是2，与第一个位置的元素5交换位置，那第一个5和中间的5的顺序就变量，所以就不稳定了。正因如此，相对于冒泡排序和插入排序，选择排序就稍微逊色了。

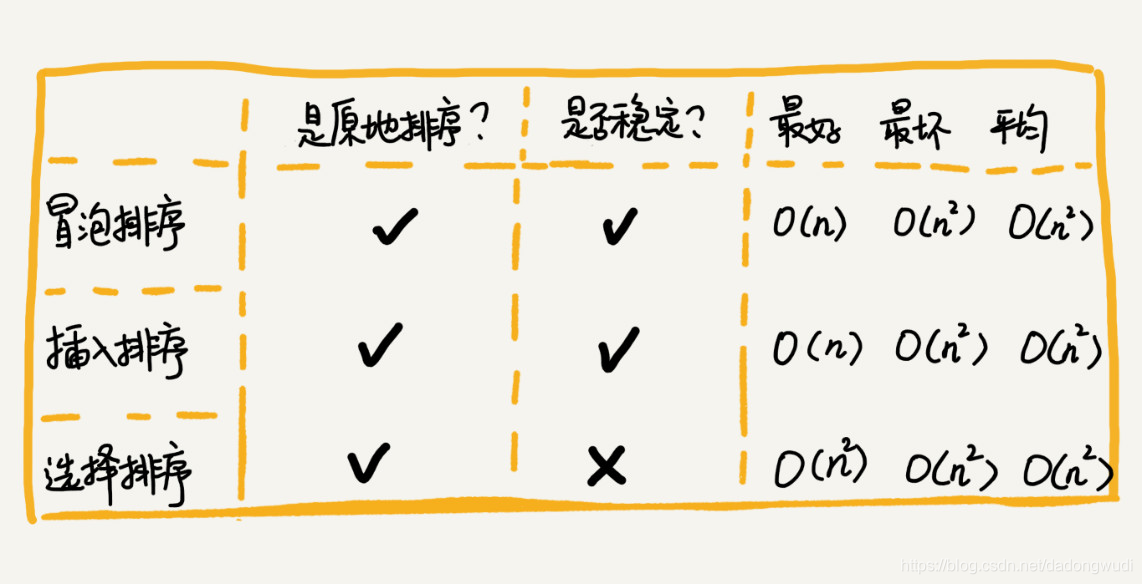
五、冒泡排序和插入排序的时间复杂度都是 O(n^2)，都是原地排序算法，为什么插入排序要比冒泡排序更受欢迎呢？

冒泡排序移动数据有3条赋值语句，而选择排序的交换位置的只有1条赋值语句，因此在有序度相同的情况下，冒泡排序时间复杂度是选择排序的3倍，所以，选择排序性能更好。

冒泡排序中数据的交换操作：
if (a[j] > a[j+1]) { // 交换int tmp = a[j];a[j] = a[j+1];a[j+1] = tmp;flag = true;
}插入排序中数据的移动操作：
if (a[j] > value) {a[j+1] = a[j];  // 数据移动
} else {break;
}

笔记整理来源： 王争 数据结构与算法之美