[Leetcode][第336题][JAVA][回文对][暴力][HashSet][字典树]

【问题描述】[困难]

在这里插入图片描述

【解答思路】

1. 暴力（超时）

时间复杂度：O(n ² ×m)，其中 n 是字符串的数量，m 是字符串的平均长度空间复杂度：O(1)

class Solution {public List<List<Integer>> palindromePairs(String[] words) {List<List<Integer>> ans = new ArrayList<>();int n = words.length;for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {if (i == j) continue;if (!check(words[i]+words[j])) continue;List<Integer> temp = new ArrayList<>();temp.add(i); temp.add(j);ans.add(temp);}}return ans;}private boolean check(String s) {int i = 0, j = s.length()-1;while (i < j) {if (s.charAt(i) != s.charAt(j)) return false;i++; j--;}return true;}
}

2. HashSet优化字典树优化

在这里插入图片描述
HashSet优化
时间复杂度：O(n * m^2)，其中 n 是字符串的数量，m是字符串的平均长度。空间复杂度：O(n)

class Solution {List<String> wordsRev = new ArrayList<String>();Map<String, Integer> indices = new HashMap<String, Integer>();public List<List<Integer>> palindromePairs(String[] words) {int n = words.length;for (String word: words) {wordsRev.add(new StringBuffer(word).reverse().toString());}for (int i = 0; i < n; ++i) {indices.put(wordsRev.get(i), i);}List<List<Integer>> ret = new ArrayList<List<Integer>>();for (int i = 0; i < n; i++) {String word = words[i];int m = words[i].length();if (m == 0) {continue;}for (int j = 0; j <= m; j++) {//左是反转 右是回文串 if (isPalindrome(word, j, m - 1)) {int leftId = findWord(word, 0, j - 1);if (leftId != -1 && leftId != i) {ret.add(Arrays.asList(i, leftId));}}//右是反转 左是回文串 if (j != 0 && isPalindrome(word, 0, j - 1)) {int rightId = findWord(word, j, m - 1);if (rightId != -1 && rightId != i) {ret.add(Arrays.asList(rightId, i));}}}}return ret;}public boolean isPalindrome(String s, int left, int right) {int len = right - left + 1;for (int i = 0; i < len / 2; i++) {if (s.charAt(left + i) != s.charAt(right - i)) {return false;}}return true;}public int findWord(String s, int left, int right) {return indices.getOrDefault(s.substring(left, right + 1), -1);}
}

字典树优化

class Solution {class Node {int[] ch = new int[26];int flag;public Node() {flag = -1;}}List<Node> tree = new ArrayList<Node>();public List<List<Integer>> palindromePairs(String[] words) {tree.add(new Node());int n = words.length;for (int i = 0; i < n; i++) {insert(words[i], i);}List<List<Integer>> ret = new ArrayList<List<Integer>>();for (int i = 0; i < n; i++) {int m = words[i].length();for (int j = 0; j <= m; j++) {if (isPalindrome(words[i], j, m - 1)) {int leftId = findWord(words[i], 0, j - 1);if (leftId != -1 && leftId != i) {ret.add(Arrays.asList(i, leftId));}}if (j != 0 && isPalindrome(words[i], 0, j - 1)) {int rightId = findWord(words[i], j, m - 1);if (rightId != -1 && rightId != i) {ret.add(Arrays.asList(rightId, i));}}}}return ret;}public void insert(String s, int id) {int len = s.length(), add = 0;for (int i = 0; i < len; i++) {int x = s.charAt(i) - 'a';if (tree.get(add).ch[x] == 0) {tree.add(new Node());tree.get(add).ch[x] = tree.size() - 1;}add = tree.get(add).ch[x];}tree.get(add).flag = id;}public boolean isPalindrome(String s, int left, int right) {int len = right - left + 1;for (int i = 0; i < len / 2; i++) {if (s.charAt(left + i) != s.charAt(right - i)) {return false;}}return true;}public int findWord(String s, int left, int right) {int add = 0;for (int i = right; i >= left; i--) {int x = s.charAt(i) - 'a';if (tree.get(add).ch[x] == 0) {return -1;}add = tree.get(add).ch[x];}return tree.get(add).flag;}
}

【总结】

1. 字符串暴力前缀搜索优化困难题目一般使用字典树

2.字典树理解原理后（类比哈希表）

借助散列表的思想，我们通过一个下标与字符一一映射的数组，来存储子节点的指针。
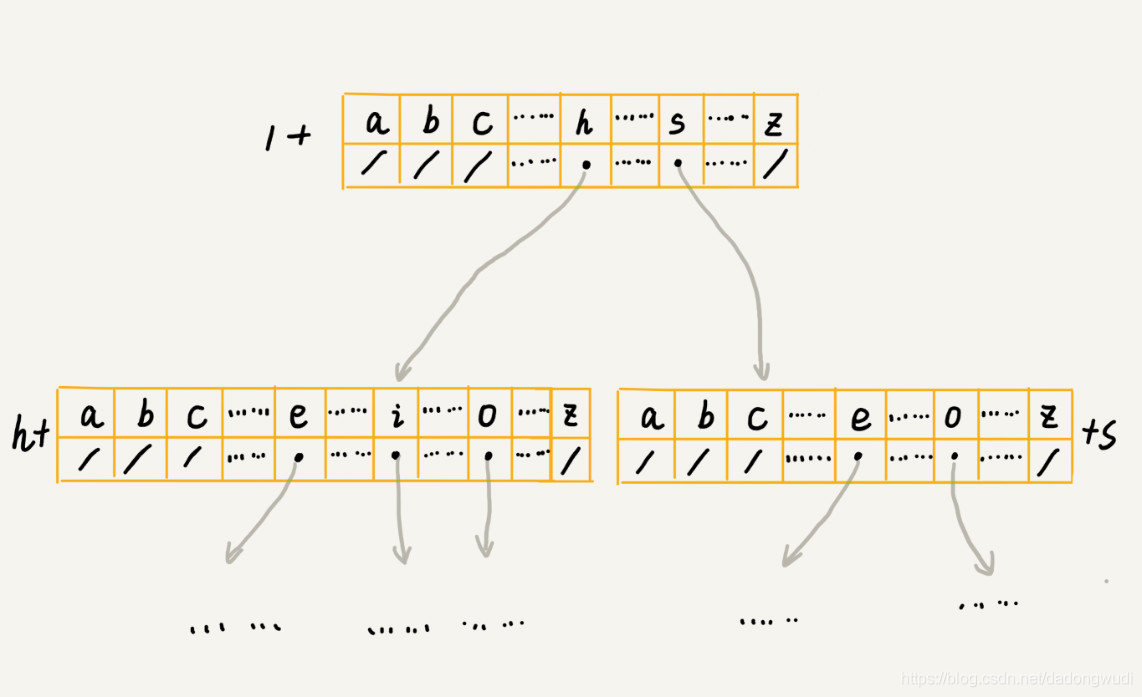
在这里插入图片描述

3.需要懂得字典树插入和搜索的代码


public class Trie {private TrieNode root = new TrieNode('/'); // 存储无意义字符// 往Trie树中插入一个字符串public void insert(char[] text) {TrieNode p = root;for (int i = 0; i < text.length; ++i) {int index = text[i] - 'a';if (p.children[index] == null) {TrieNode newNode = new TrieNode(text[i]);p.children[index] = newNode;}p = p.children[index];}p.isEndingChar = true;}// 在Trie树中查找一个字符串public boolean find(char[] pattern) {TrieNode p = root;for (int i = 0; i < pattern.length; ++i) {int index = pattern[i] - 'a';if (p.children[index] == null) {return false; // 不存在pattern}p = p.children[index];}if (p.isEndingChar == false) return false; // 不能完全匹配，只是前缀else return true; // 找到pattern}public class TrieNode {public char data;public TrieNode[] children = new TrieNode[26];public boolean isEndingChar = false;public TrieNode(char data) {this.data = data;}}
}