贪心算法
回溯算法
分治算法
动态规划

四种基本的算法思想：贪心算法，分治算法，回溯算法，动态规划，他们不是具体算法，常用来指导我们设计具体的算法和编码等。

一：贪心算法有很多经典应用

霍夫曼编码（Huffman Coding）,Prim和Kruskal最小生成数算法，Dijkstra单源最短路径算法。

二：如何理解“贪心算法”

假设我们有一个可容纳100kg物品的背包，可以装下各种物品，我们有以下5中豆子，每种豆子的总量和总价值都各不相同。为了让背包中所装物品的总价最大，该如何？

第一步：当我们看到这类问题时，首先要联想到贪心算法：针对一组数据，定义了限制值和期望值，系统从中选出几个数据，在满足限制值的情况下，期望值最大。
第二步：尝试看这个问题是否可以用贪心算法解决：每次选择当前情况下，在对限制值同等贡献量的情况下，对期望值贡献最大的数据。
第三步：举几个例子看下贪心算法产生的结果是否最优的。大部分情况下，举几个例子验证一下就可以了。严格的证明贪心算法的正确性，非常复杂，需要涉及较多的数学推理。并且，从实践的角度来说，大部分能用贪心算法的问题，贪心算法的正确性都是显而易见的，月不需要严格的数学推导证明。

贪心算法，专注于当下最优，但可能无法取得全局最优。

贪心算法实战分析

一：分糖果

有m个糖果和n个孩子，但m<n，所以糖果只能分配给一部分孩子。
每个糖果的大小不等，分为s1，s2……sm。除此之外，每个孩子对糖果大小的需求也是不一样的，只有糖果的大小>=孩子对糖果大小的需求分别是g1，g2，g3……gn。
如何分配才可能满足最多数量的孩子？

可将这个问题抽象成：从n个孩子中抽取一部分孩子分配糖果，让满足的孩子个数（期望值）是最大的。这个问题的限制值就是糖果个数m。

对于一个孩子而言，如果小的糖果可以满足，我们就没必要用更大的糖果，这样更大的就可以留给其他对糖果大小需求更大的孩子。另一方面，对糖果大小需求小的孩子更容易被满足，所以，我们可以从需求小的孩子开始分配他糖果。因为满足一个需求大的孩子跟满足一个需求小的孩子，对我们期望值贡献是一样的。

二：钱币找零（部分题目不适用 100 99 1 找396 ）

假设有1元，2元，5元，10元，50元，100元这些面额的纸币，他们的张数分别是c1，c2，c5，c10，c20，c50，c100。我们要有支付k元，最少要用多少张纸币呢？

在贡献相同期望值（纸币数目）的情况下，我们希望多贡献点金额，这样就可以让纸币数更少。这就是一种贪心算法的解决思路。

三：区间覆盖

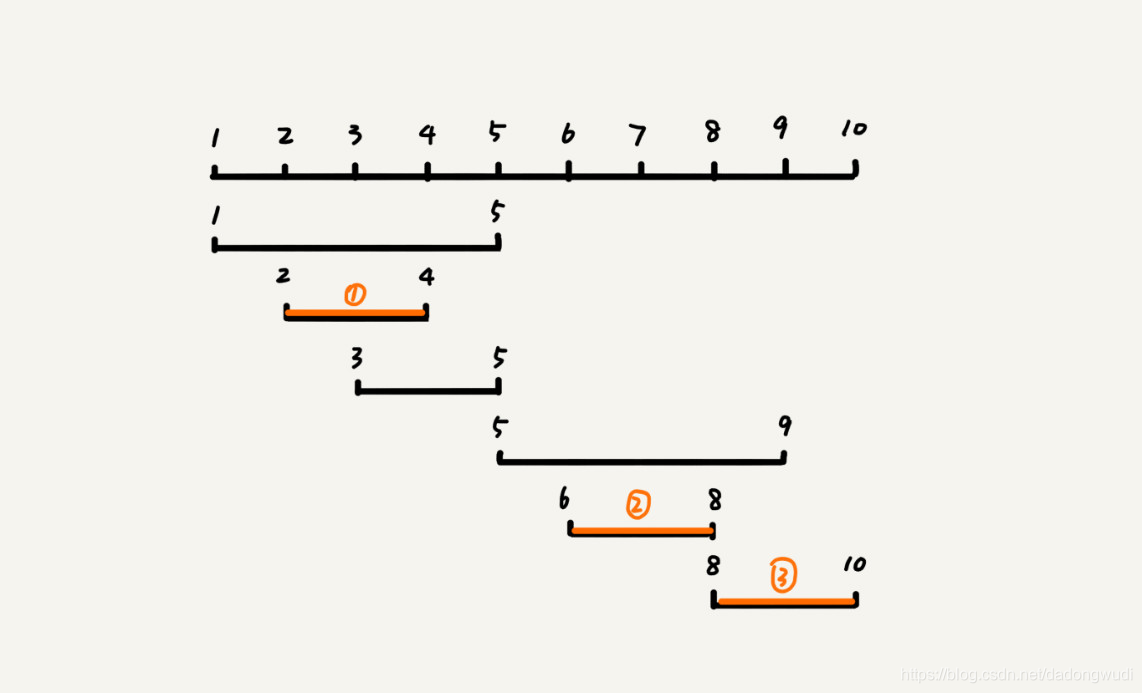
假设有n个区间，区间的起始端点和结束端点分分别是[l1,r1]，[l2，r2]，[l3,r3]……，从n个区间中选出一部分区间，这部分区间满足两两不相交（端点相交的情况不算相交），最多能选出多少个区间？

我们假设这 n 个区间中最左端点是 lmin，最右端点是 rmax。这个问题就相当于，我们选择几个不相交的区间，从左到右将[lmin, rmax]覆盖上。我们按照起始端点从小到大的顺序对这 n 个区间排序。
我们每次选择的时候，左端点跟前面的已经覆盖的区间不重合的，右端点又尽量小的，这样可以让剩下的未覆盖区间尽可能的大，就可以放置更多的区间。这实际上就是一种贪心的选择方法。

四：如何用贪心算法实现霍夫曼编码？

假设有一个包含1000个字符的文件，每个字符占1个byte（1byte=8bits），存储这1000个字符就一共需要8000bits。
但使用霍夫曼编码，可实现压缩率在20%~90%之间。
霍夫曼编码不仅会考察文本汇总有多少个不同字符，还会考察每个字符出现的频率，根据频率的不同，选择不同长度的编码。霍夫曼编码试图用这种不等长的编码方法，来进一步增加压缩的效率。
根据贪心的思想，可以把出现频率比较多的字符，用稍微短一些的编码；出现频率比较少的字符，用稍微长一些的编码。
由于霍夫曼编码是不等长的，每次应该读取1为还是2位，3位等来解压缩是个问题，这个问题导致霍夫曼编码解压缩比较复杂。
为了避免解压缩过程中的歧义，霍夫曼编码要求各个字符的编码之间，不会出现某个编码是另一个编码前缀的情况。

假设这6个字符出现的频率从高到低依次是a，b，c，d，e，f。我们把它们编码下面这个样子，任何一个字符的编码都不是另一个的前缀，在解压缩的时候，我们每次会读取尽可能长的可解压缩的二进制，所以在解压缩的时候也不歧义。

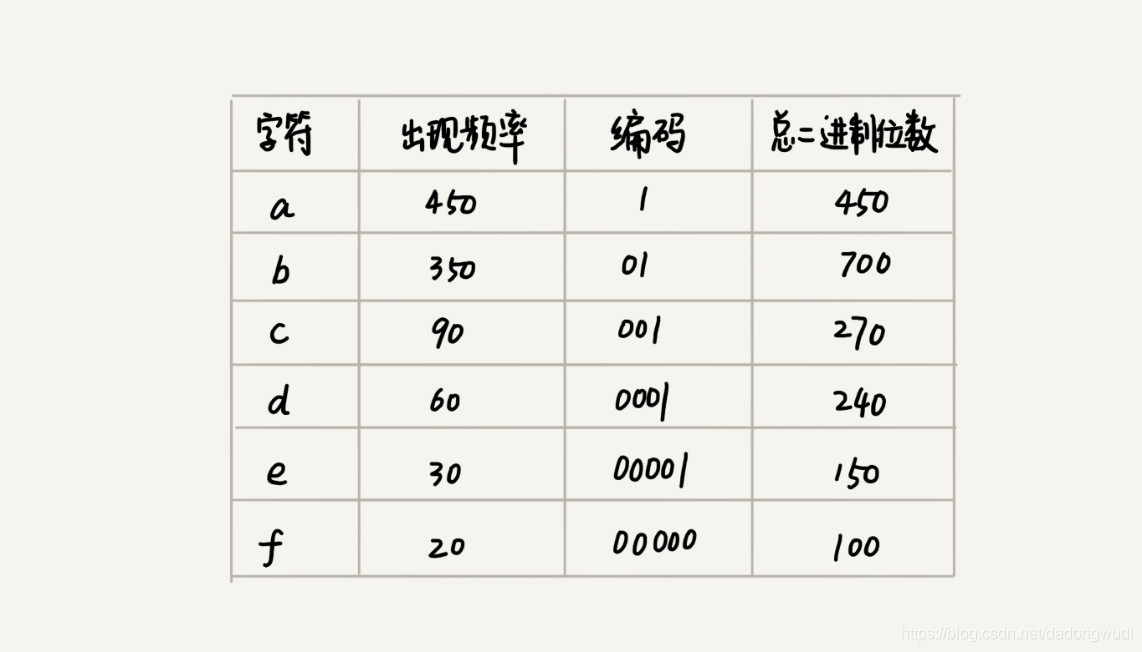
根据字符出现频率的不同，给不同的字符进行不同长度的编码的实现方式
把每个字符看作一个节点，并且辅带着把频率放到优先级队列中。从队列中取出频率最小的两个节点A,B，然后新建一个节点C，把频率设置为两个节点的频率之和，并把这个新节点C作为节点A,B的父节点。最后再把C节点放入到优先级队列中。重复这个过程，直到队列中没有数据。

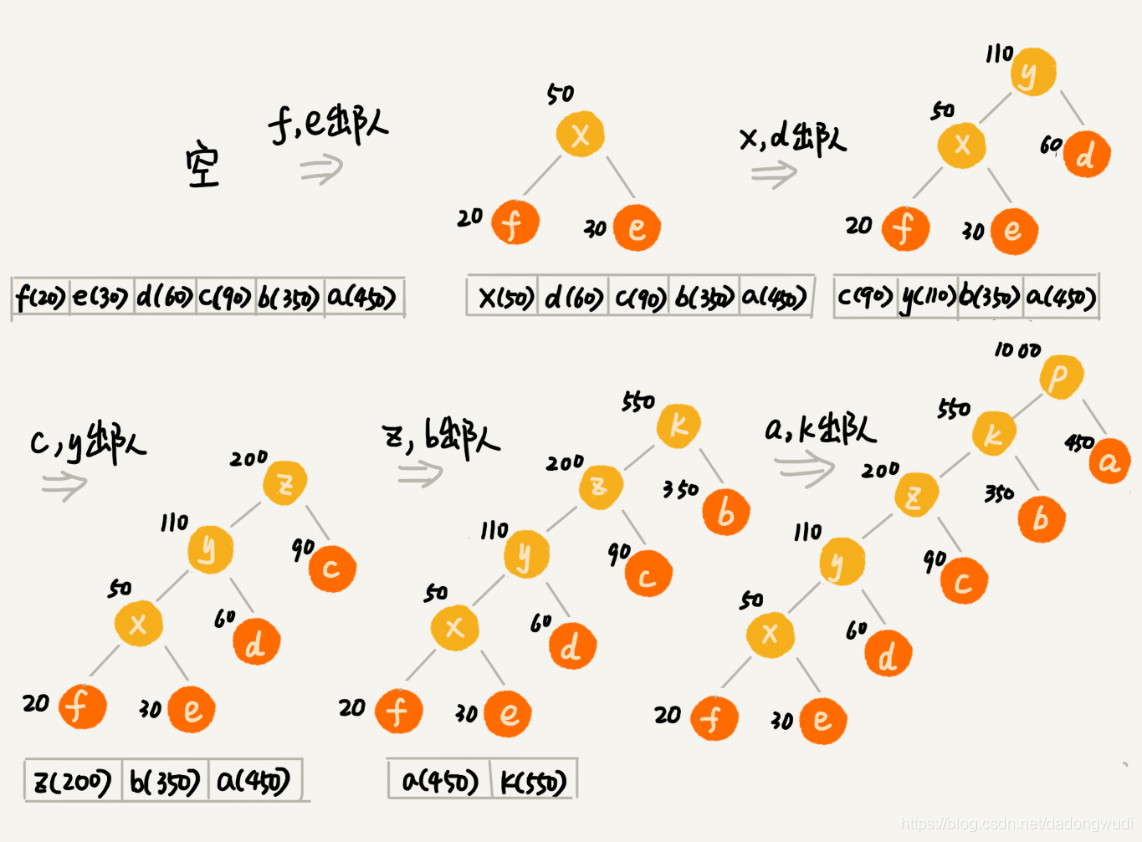
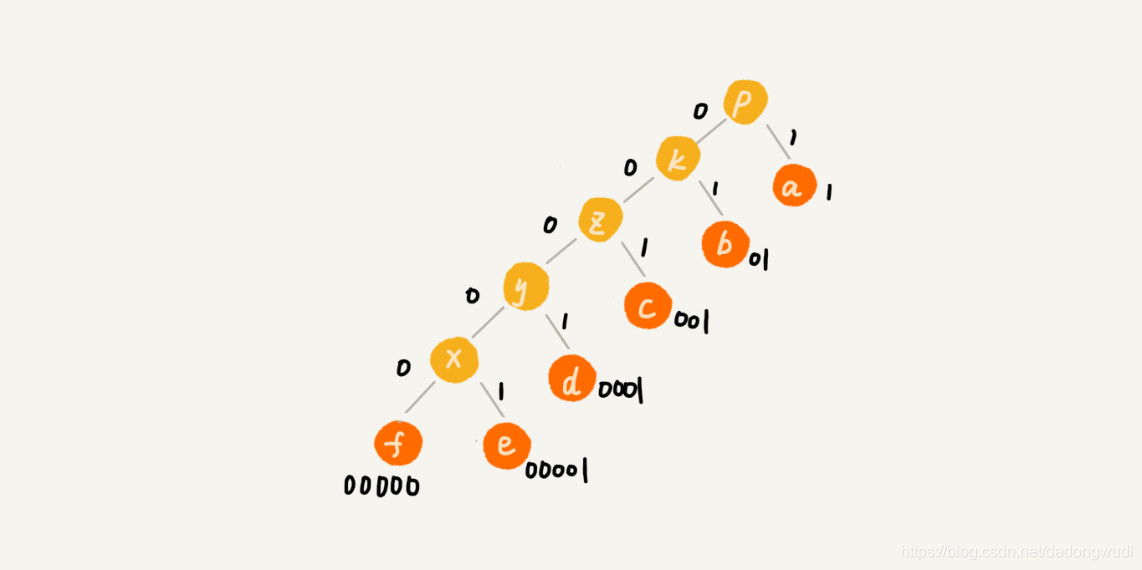
給每一条边画上一个权值，指向左子节点的边，我们统统标记为0，指向右子节点的边，我们统统标记为1，那从根节点到叶节点的路径就是叶节点对应字符的霍夫曼编码

笔记整理来源： 王争 数据结构与算法之美