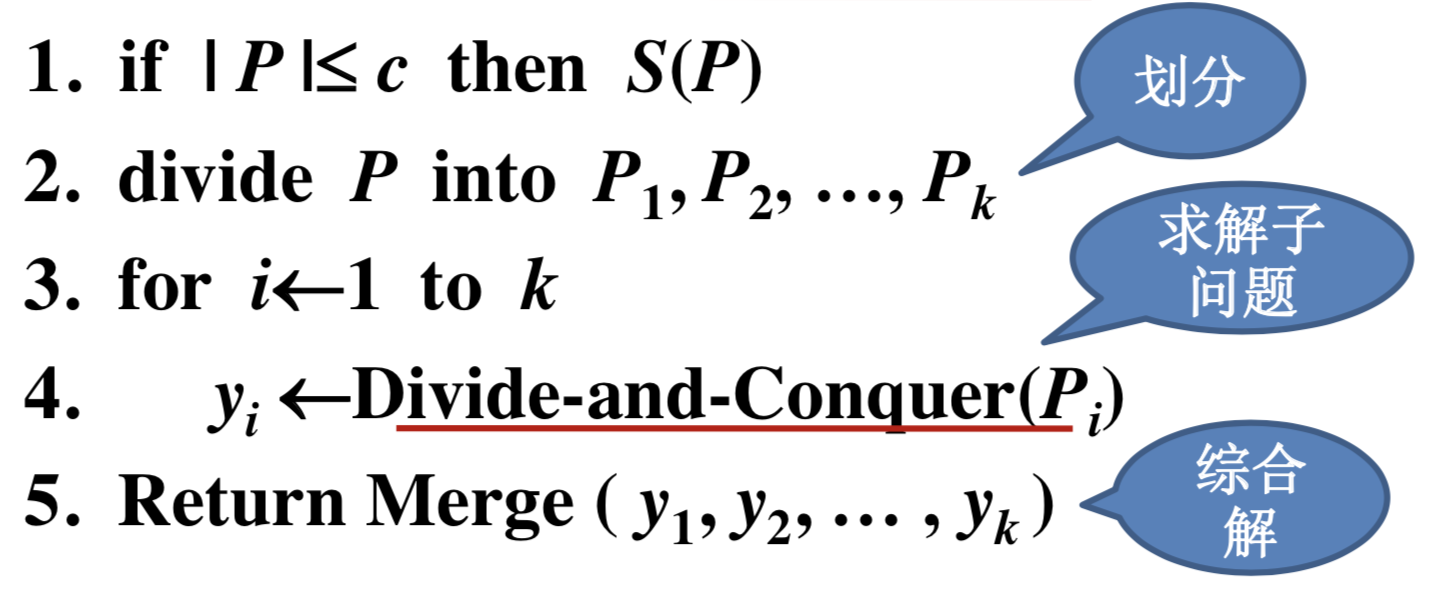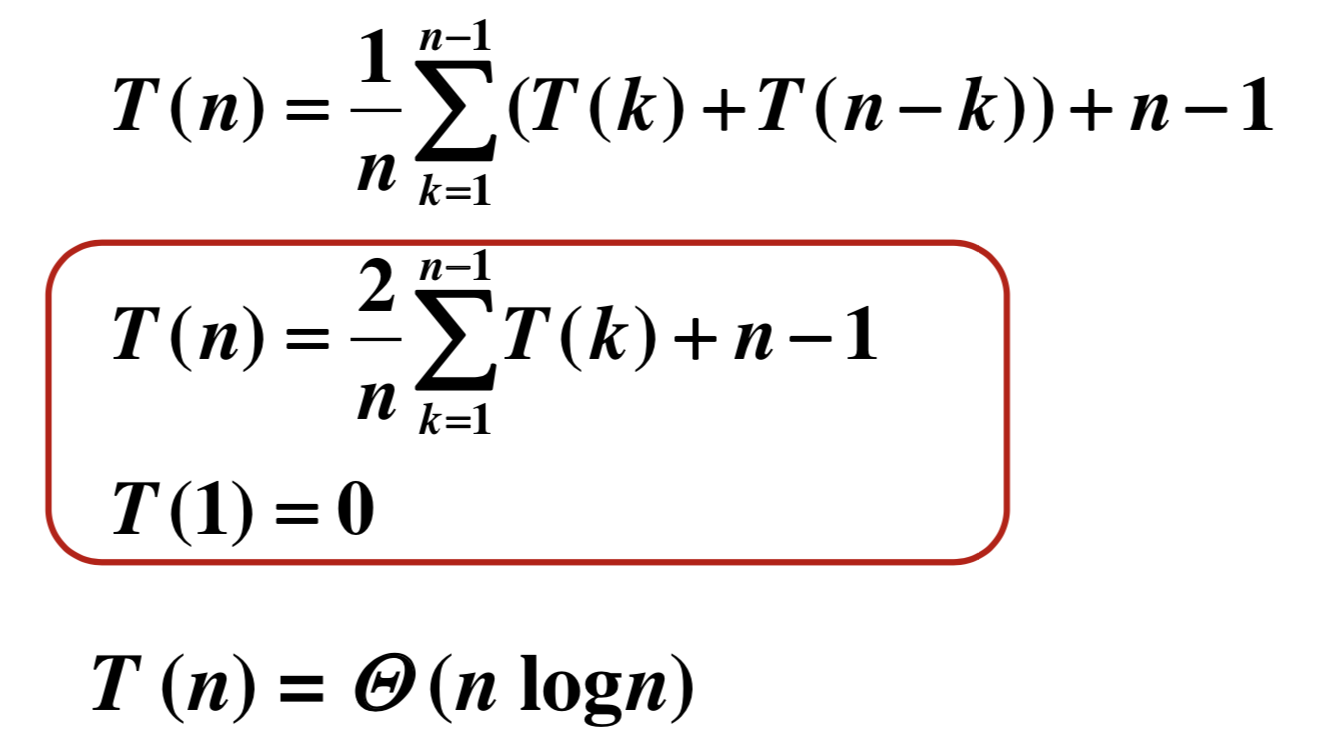主定理是一个非常有用的定理,前面我们学习的所有知识都可以用主定理来求解,而不必要使用复杂的计算方法来求解
文章目录
- 1. 主定理
- 1.1 主定理的应用背景
- 1.2 主定理内容
- 2. 主定理的应用
- 2.1 求解递推方程 例1
- 2.2 求解递推方程 例2
- 2.3 求解递推方程 例3
- 3. 总结
1. 主定理
1.1 主定理的应用背景
求解递推方程:
其中:
- a: 归约后的子问题个数
- n/b:归约后子问题的规模
- f(n):归约过程及组合子问题的解的工作量
例如前面的文章我们曾求解过:
- 二分检索: T(n) = T(n/2)+1
- 二分归并排序: T(n) =2T(n/2)+n-1
现在想要求解这些式子,不再像以前那样采用各种技巧进行求解,可以直接通过主定理进行求解:
1.2 主定理内容
定理:设a >= 1, b>1为常数, f(n)为函数, T(n) 为非负整数,且T(n)=aT(n/b)+f(n), 则:
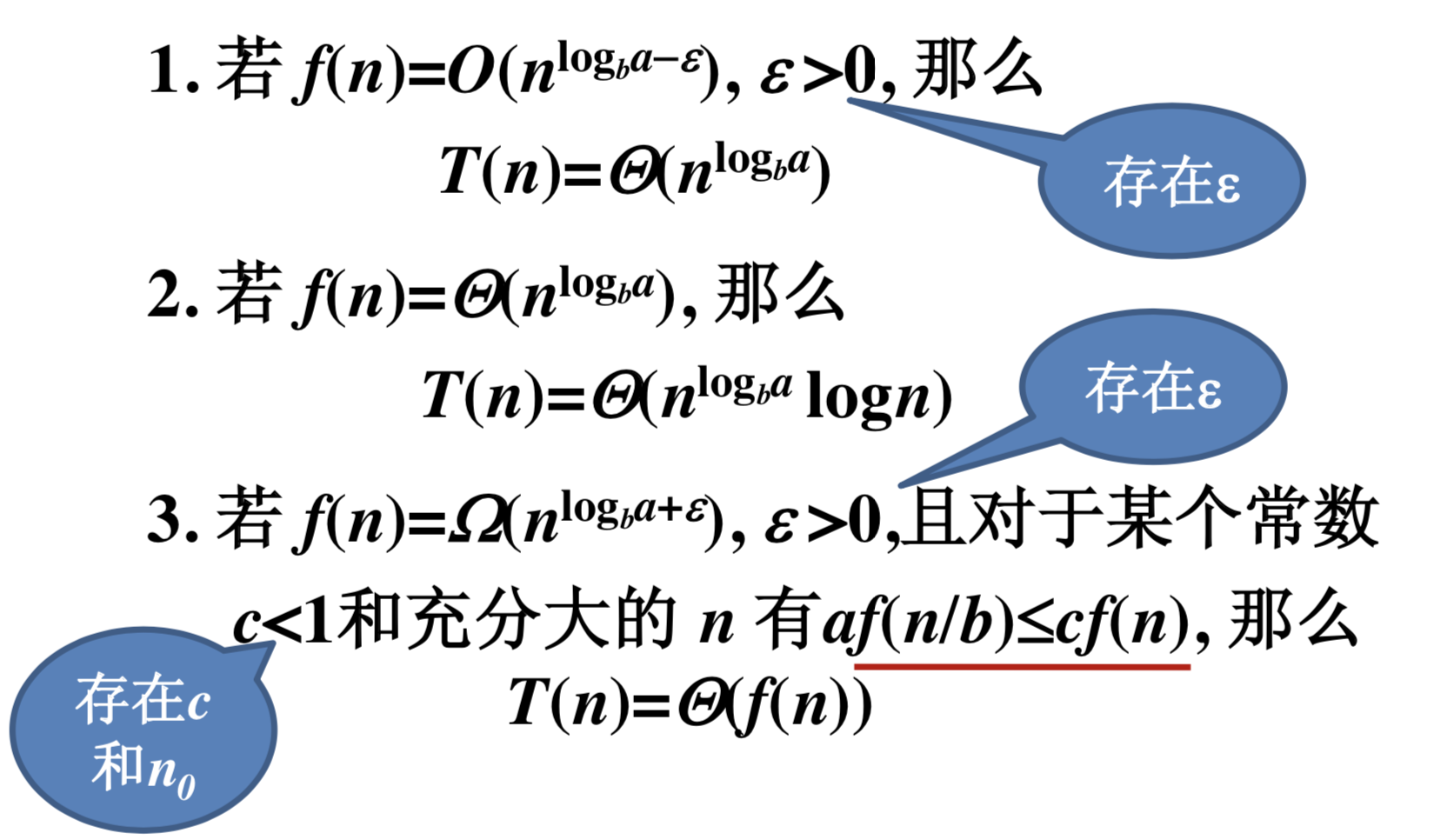
主定理的证明过程略
2. 主定理的应用
2.1 求解递推方程 例1
T(n) = 9T(n/3) + n
上述递推方程中:
a = 9, b = 3,f (n) = n,所以:
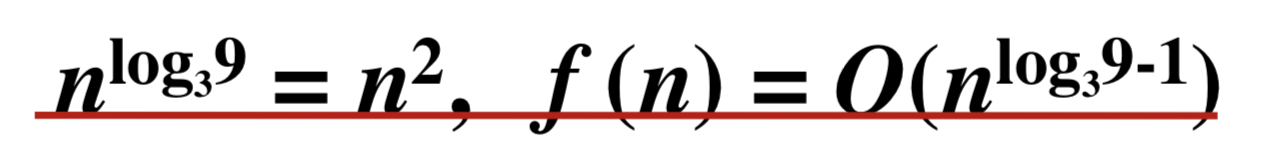
相当于主定理的case1,其中ξ\xiξ =1.
根据定理得到 T(n) = Θ\ThetaΘ (n2)
2.2 求解递推方程 例2
T(n) = T(2n/3) + 1
上述递推方程中的
a = 1, b = 3/2, f(n) = 1,
nlog3/21=n0=1n^{log_{3/2}1} = n_0 = 1nlog3/21=n0=1
相当于主定理的Case2 .
根据定理得到T(n) = Θ\ThetaΘ( log n)
2.3 求解递推方程 例3
求解递推方程
T(n) = 3T(n/4) + nlogn
上述递推方程中的
a=3, b=4, f(n)=nlogn
所以: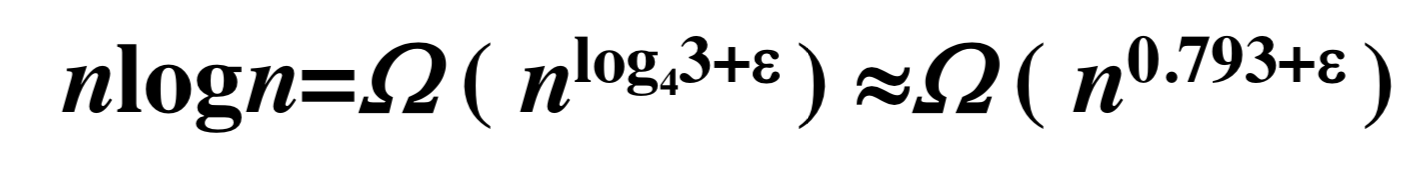
取 = 0.2 即可.
ξ\xiξ =0.2即可
条件验证:

3. 总结
对于之前的二分搜索则对应主定理的case2,二分归并排序则也对应主定理的case2,可以直接利用主定理求解。
但是也有很多时候不能使用主定理,如果不能使用,就使用递归树或者迭代法等方法求解。