上一篇文章学习了：【算法设计与分析】15 分治策略：芯片测试

1. 快速排序的基本思想

• 用首元素 x 作划分标准，将输入数 组 A划分成不超过 x 的元素构成的数 组 A_L，大于 x 的元素构成的数组 A_R. 其中 A_L, A_R从左到右存放在数组 A 的位置.
• 递归地对子问题 A_L和 A_R 进行排序， 直到子问题规模为 1 时停止.

下面两张图是它的伪代码表示：

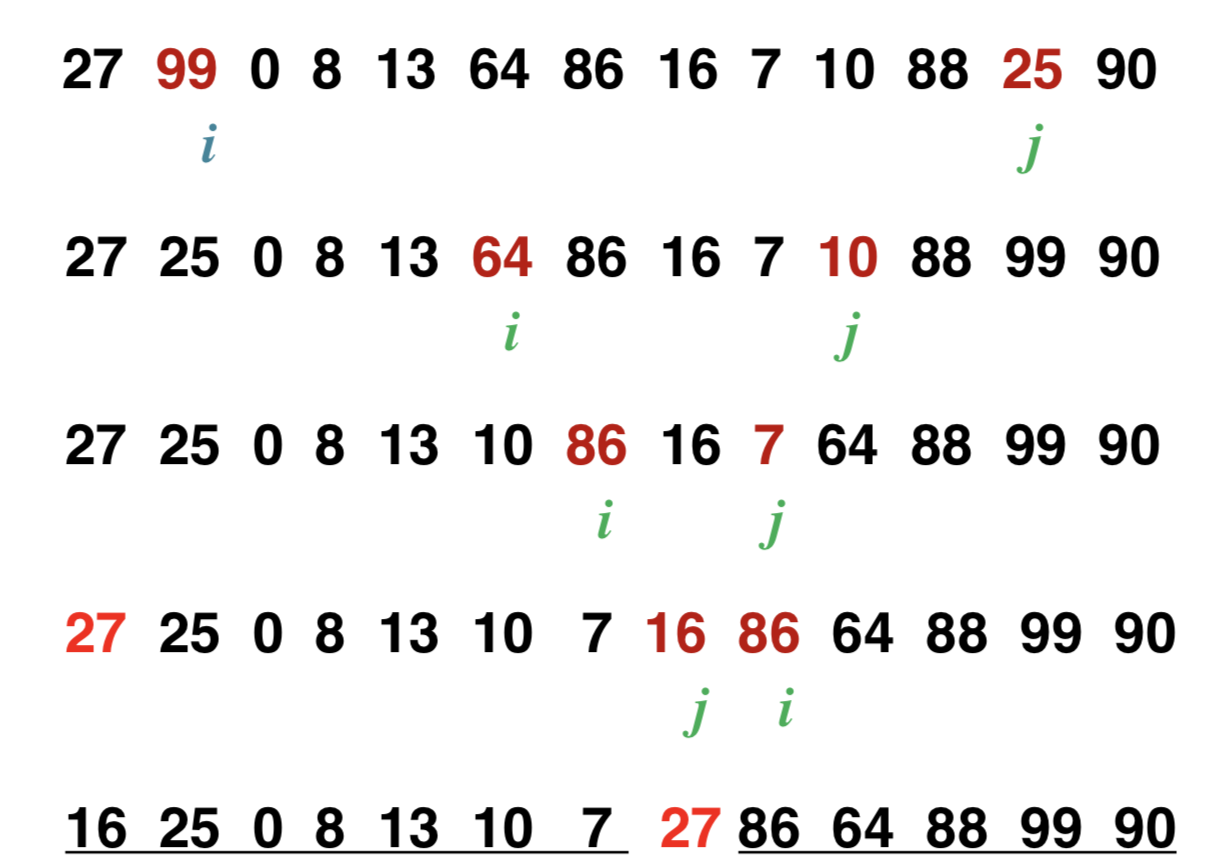
划分的过程为：

以下是划分的例子：

1.2 时间复杂度的计算

1.21 最坏情况时间复杂度计算

最坏情况:

• W(n) = W(n-1)+n-1
• W(1) = 0

得出：

• W(n) = n(n-1)/2

在最坏情况下，有一种可能为：每次划分，首元素依然是在首元素，它是最小的（或者是最大的），下次划分也是同样的结果。这种情况下，是最坏的情况。子问题永远比上一个原问题只少了一个元素。并且每次都需要对n-1个元素进行遍历比较。

由上面的结果看出最坏的情况的时间复杂度是O(n²)

1.22 最好情况时间复杂度

最好情况下，就是每一次划分，A_L 与A_R 总是均衡的在两边，首元素最终落到中间。那么子问题就变成了原问题的一半的元素数量(但是有两个子问题)。

• T(n) = 2 T(n/2)+n-1
• T(1) = 0

得出：
$T(n)=\Theta (nlogn)$

以上两种时间复杂度是最好和最坏的情况下。那么均衡额时间复杂度如何计算呢？

在计算均衡时间复杂度之前先来看看划分之后A_L 与 A_R 的比例是固定时的时间复杂度是多少？

例如子问题的规模比是1：9时，那么有：

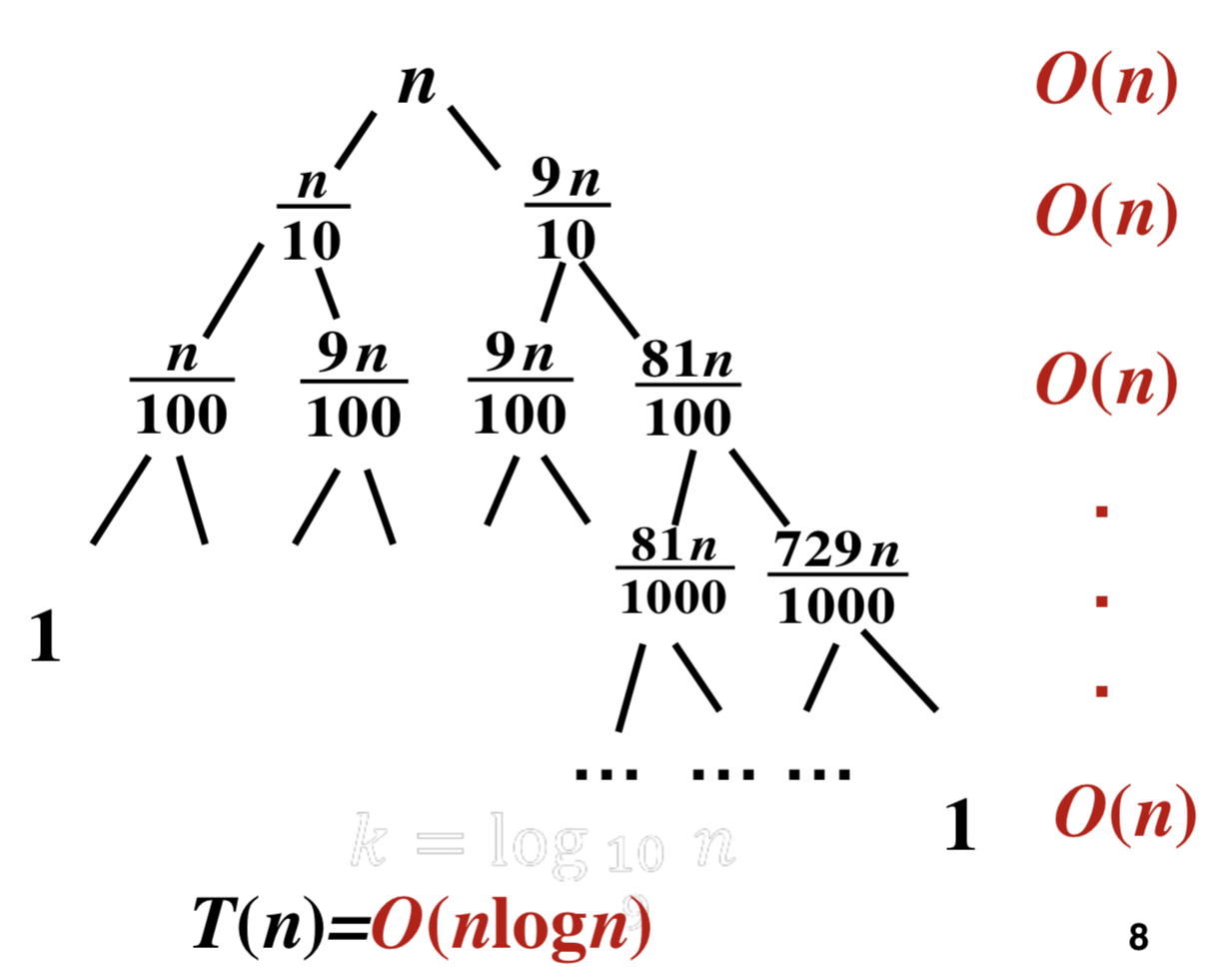
• T(n) = T(n/10) + T(9n/10) + n
• T(1) = 0

根据递归树，时间复杂度为:

• $T(n)=\Theta (nlogn)$

注释，上面的递归树计算如下：

1.23 平均时间复杂度计算

那么平均时间复杂度计算如下：

首元素最后落在的位置，可能在1，2，3…n

假设情况的概率均为1/n，那么各个情况下，子问题的计算规模如下：

• 首元素在位置 1: T(0), T(n-1)
• 首元素在位置 2: T(1), T(n-2)

…

• 首元素在位置 n-1: T(n-2), T(1)
• 首元素在位置 n: T(n-1), T(0)

那么子问题的工作量一共为：2[T(1)+T(2)+…+T(n-1)]

划分工作量 n-1

那么平均情况下时间复杂度计算公式为：

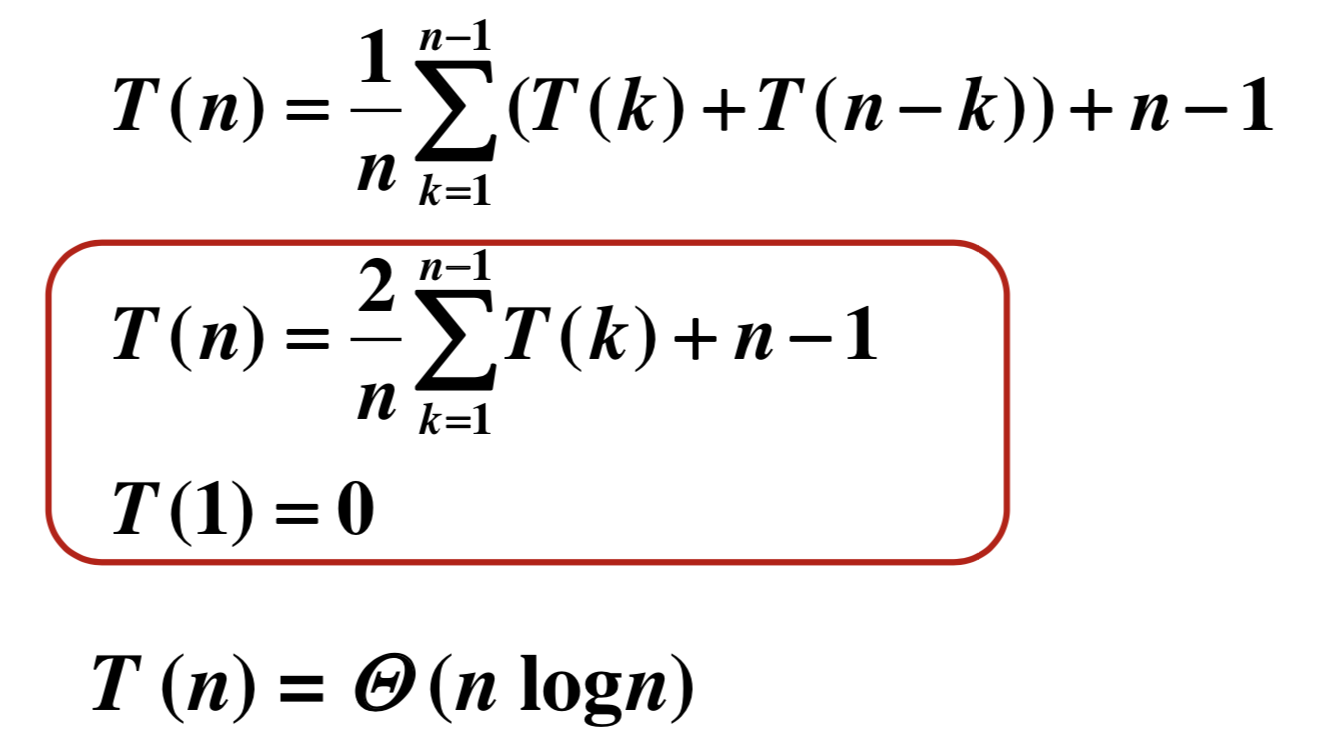
首元素划分后每个位置概率相等

2 总结

快速排序一般人都能写出来，但是要理解它的时间复杂度计算，恐怕并不是一般人都会计算，我们要追根问底。

快速排序算法
• 分治策略
• 子问题划分是由首元素决定 • 最坏情况下时间O(n²)
• 平均情况下时间为O(nlogn)