随机微分方程,俗称SDE,相信点进来的同学们肯定对这个概念不感到陌生。SDE呢,是对现实生活中一些随机波动的事物的建模,比如可以用几何布朗运动(GBM)来模拟股价变化,用CIR模型来模拟利率波动。
然而一个很现实的问题就是,如何对SDE进行参数估计?就是,对于一个给定的含有参数的SDE,给出一些轨道,然后想要估计出参数的值来。比如已知一只股票的历史价格数据,假定它服从GBM,怎么近似求出它的期望收益率
知乎上还没有人专门讨论过这个问题,最近看了几篇这个主题的论文,所以我来抛砖引玉了。
问题的标准形式
对于含参的扩散方程:
设
扩散问题参数估计的标准形式是:已知过程
极大似然估计法
面对参数估计的问题自然就会想到极大似然法,在矩估计不好用的时候,极大似然估计是点估计比较好的选择。
由于给出的观测点都是离散的,设
现在麻烦的事情是这个转移概率密度怎么计算,有了它才能求似然解对不对!?
EML
事实上,转移概率密度满足如下PDE:
这个抛物PDE叫做Fokker-Planck方程,证起来比较麻烦。这个方程可是在物理学有广泛的应用的。(你看大名鼎鼎的 Planck 普朗克)
这么看,对于某些特殊的SDE,是可以从理论上求出转移密度的解析解的,继而可以精确求解极大似然函数。比如说对于CIR过程就是可以写出解析形式的转移概率密度。但是对于大多数SDE,根本没有办法解得这样一个复杂的PDE的解析解,但是退一步,可以数值求解该PDE,或者求出一个近似的解析解来代替真正的解。硬刚一个PDE确确实实可以解决咱们的问题,在一些论文里边,这种方法叫做EML(exact maximum likelihood)。
但是硬刚PDE这种方法不好操作啊,理论艰深,操作困难,关键是咱学不会。那有没有容易一点的方法?
DML
回忆一下SDE的两种模拟方法:
- Euler-Maruyama方法:
- Milstein方法:
其中
这两种方法其实都是对SDE在一个区间上的离散近似,借助这种近似(Euler方法),我们可以认为,从
看样子问题已经有点眉目了,现在我们可以把这个转移概率密度代入到似然函数去求解似然方程啦!
这种方法借助SDE模拟的离散形式近似估计转移概率密度,因此称作DML(discret maximum likelihood)。
下面以CIR模型来说明一下如何用DML来进行估计和DML方法的效果,代码全部是用MATLAB写的。
一个生动的参数估计的例子
CIR模型:
这里面有三个参数,
一般来说,先通过第二、三个方程组得到
我们用MATLAB自带的函数来生成轨道,MATLAB对CIR模型还是有一定的支持的:
model = cir(2, 1, 0.5, 'StartState', 1);
[X, T] = model.simByEuler(100,'DeltaTime',0.01);以上第一行代码创建了一个cir类,三个参数分别是2, 1, 0.5并且起始点是1。第二行调用了这个类的simByEuler方法,以0.01s为时间间隔得到100个点,等于我们得到了一条[0,1]上以0.01为时间间隔的轨道!
接下来我写了一个用DML方法给定一条轨道求CIR模型参数估计的函数:
% DML.m
function [alpha, beta, sigma] = DML(X, T)
% 使用DML方法根据采样时间 T 和 位置 X 来估计 CIR 模型的三个参数% 别看这里符号乱,其实就是解上面那个方程组,你自己也可以写一个
d = diff(T);
A = sum(d);
B = sum(X(1: end-1) .* d);
C = X(end) - X(1);
D = sum(d ./ X(1: end-1));
E = sum(diff(X) ./ X(1: end-1));beta = (B - C / E * A) / (A - C / E * D);
alpha = E / (beta * D - A);sigma = sqrt( mean( (...(diff(X) - alpha * (beta - X(1: end-1)) .* d ) .^ 2 ./ (X(1: end-1) .* d))));
endok,三个参数的真实值还是取为2, 1, 0.5,我们用上面的那个cir类来模拟200条轨道,然后对结果求平均数:
DML_a = []; % alpha
DML_b = []; % beta
DML_s = []; % sigma
for i = 1 : 200[X, T] = model.simByEuler(100,'DeltaTime',0.01);[alpha, beta, sigma] = DML(X, T);DML_a = [DML_a alpha];DML_b = [DML_b beta];DML_s = [DML_s sigma];
end200条轨道得到了200个参数的估计值,其结果的分布如图:
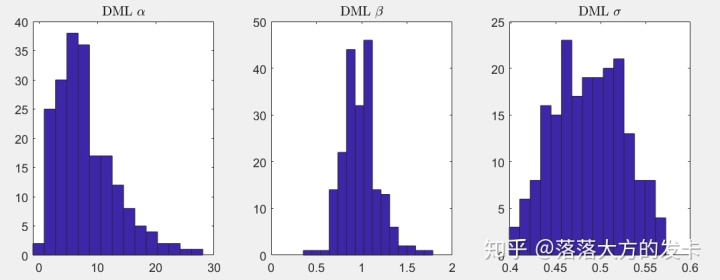
一开始看到这个结果我以为我代码敲错了,因为
DML估计法其实是个有偏估计,从上面的
Conclusion
本文提出了一般形式的随机微分方程的参数估计问题,对于其参数的极大似然估计方法提出了EML和DML两种思路,并针对比较好实现的DML方法给出了CIR模型参数估计的代码和示例。
接下来一篇文章我会分析DML方法的不足之处,并介绍一些能够改进DML方法的思路。
)




)



)
)



)

![[Java]向上/下转型Casting](http://pic.xiahunao.cn/[Java]向上/下转型Casting)


