4182: Shopping
Time Limit: 30 Sec Memory Limit: 128 MB
Submit: 374 Solved: 130
[Submit][Status][Discuss]
Description
马上就是小苗的生日了，为了给小苗准备礼物，小葱兴冲冲地来到了商店街。商店街有n个商店，并且它们之间的道路构成了一颗树的形状。
第i个商店只卖第i种物品，小苗对于这种物品的喜爱度是wi，物品的价格为ci，物品的库存是di。但是商店街有一项奇怪的规定：如果在商店u,v买了东西，并且有一个商店w在u到v的路径上，那么必须要在商店w买东西。小葱身上有m元钱，他想要尽量让小苗开心，所以他希望最大化小苗对买
到物品的喜爱度之和。这种小问题对于小葱来说当然不在话下，但是他的身边没有电脑，于是他打电话给同为OI选手的你，你能帮帮他吗？
Input
输入第一行一个正整数T，表示测试数据组数。
对于每组数据，
第一行两个正整数n;m；
第二行n个非负整数w1,w2...wn；
第三行n个正整数c1,c2...cn；
第四行n个正整数d1,d2...dn；
接下来n-1行每行两个正整数u;v表示u和v之间有一条道路
Output
输出共T 行，每行一个整数，表示最大的喜爱度之和。
Sample Input
1 3 2 1 2 3 1 1 1 1 2 1 1 2 1 3
Sample Output
4
HINT
N<=500,M<=4000,T<=5,Wi<=4000,Di<=100
分析：
题意：两个点选了，它路径上的点必须选。求树上一个联通块的多重背包，权值最大。
题解：
先用点分治假设重心必选，然后dfs它子树，这样每个点会做背包的次数降低到log次。
然后dfs子树时列出dfs序，然后转移方程：
对于第二步，多重背包优化可以考虑二进制拆分总复杂度为O（Tnmlognlogm）。
也可以使用单调队列优化总复杂度O(Tnmlogn)
下面是对单调队列优化的图解：
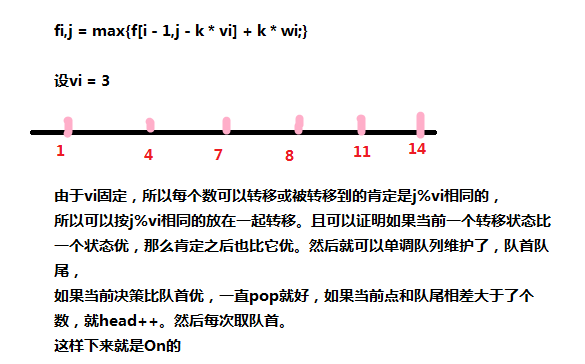
嗯。。没了。
AC代码：
# include <cstdio> # include <cstring> # include <iostream> # include <algorithm> using namespace std; const int N = 4e3 + 12; const int M = 5e3 + 12; int mx[N],w[N],v[N],c[N],n,m,root,head[N],dt,sz[N],sum,id[N],ed[N],ans; int f[N][M]; bool vis[N]; struct Edge{int to,nex; }edge[N << 1]; void AddEdge(int u,int v) {edge[++dt] = (Edge){v,head[u]};head[u] = dt; } void find(int u,int pre) {mx[u] = 0;sz[u] = 1;for(int i = head[u];i;i = edge[i].nex){if(vis[edge[i].to] || edge[i].to == pre)continue;find(edge[i].to,u);sz[u] += sz[edge[i].to];mx[u] = max(mx[u],sz[edge[i].to]);}mx[u] = max(mx[u],sum - sz[u]);if(mx[u] < mx[root])root = u; } void dfs(int u,int pre) {sz[u] = 1;id[++dt] = u;for(int i = head[u];i;i = edge[i].nex){if(vis[edge[i].to] || edge[i].to == pre)continue;dfs(edge[i].to,u);sz[u] += sz[edge[i].to];}ed[u] = dt; } int Q1[M],Q2[M]; void calc(int *g,int x) {int h1,h2,t1,t2,cnt,t;for(int j = 0;j < v[x];j++){h1 = t1 = h2 = t2 = cnt = 0;for(int k = j;k <= m;k += v[x]){if(t1 - h1 == c[x] + 1){if(Q2[h2 + 1] == Q1[h1 + 1])++h2;++h1;}t = g[k] - cnt * w[x];Q1[++t1] = t;while(h2 < t2 && Q2[t2] < t)--t2;Q2[++t2] = t;g[k] = Q2[h2 + 1] + cnt * w[x];++cnt;}} } void solve() {for(int i = 1;i <= dt + 1;i++)for(int j = 0;j <= m;j++)f[i][j] = 0;int x,t;for(int i = dt;i >= 1;i--){x = id[i]; for(int j = m;j >= v[x];j--)f[i][j] = f[i + 1][j - v[x]] + w[x];calc(f[i],x);for(int j = m;j >= 0;j--)f[i][j] = max(f[i][j],f[ed[x] + 1][j]);}ans = max(ans,f[1][m]); } void dfs(int u) {vis[u] = true;dt = 0;dfs(u,-1);solve();for(int i = head[u];i;i = edge[i].nex){if(vis[edge[i].to])continue;root = 0;sum = sz[edge[i].to];if(sum > sz[u])sum = sum - sz[u];find(edge[i].to,u);dfs(root);} } int main() {mx[0] = N;int Case;scanf("%d",&Case);while(Case--){scanf("%d %d",&n,&m);int x,y;memset(vis,false,sizeof vis);memset(head,0,sizeof head);dt = ans = 0;for(int i = 1;i <= n;i++)scanf("%d",&w[i]);for(int i = 1;i <= n;i++)scanf("%d",&v[i]);for(int i = 1;i <= n;i++)scanf("%d",&c[i]),c[i]--;for(int i = 1;i < n;i++)scanf("%d %d",&x,&y),AddEdge(x,y),AddEdge(y,x);root = 0;sum = n;find(1,-1);dfs(root);printf("%d\n",ans);} }
