1886. 判断矩阵经轮转后是否一致
给你两个大小为 n x n 的二进制矩阵 mat 和 target 。现 以 90 度顺时针轮转 矩阵 mat 中的元素 若干次 ,如果能够使 mat 与 target 一致,返回 true ;否则,返回 false 。
示例 1:

输入:mat = [[0,1],[1,0]], target = [[1,0],[0,1]]
输出:true
解释:顺时针轮转 90 度一次可以使 mat 和 target 一致。
示例 2:

输入:mat = [[0,1],[1,1]], target = [[1,0],[0,1]]
输出:false
解释:无法通过轮转矩阵中的元素使 equal 与 target 一致。
示例 3:
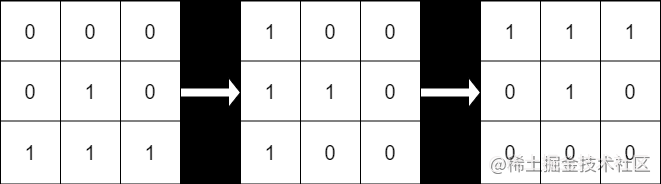
输入:mat = [[0,0,0],[0,1,0],[1,1,1]], target = [[1,1,1],[0,1,0],[0,0,0]]
输出:true
解释:顺时针轮转 90 度两次可以使 mat 和 target 一致。
提示:
- n == mat.length == target.length
- n == mat[i].length == target[i].length
- 1 <= n <= 10
- mat[i][j] 和 target[i][j] 不是 0 就是 1
解题思路
因为对于mat矩阵,我们最多只能以 90 度顺时针轮转 矩阵 mat 中的元素3次,因为第四次就会变为mat的初始状态,因此我们只需要模拟mat进行3次 90 度顺时针轮转,并且在每次轮转以后,判断一次mat矩阵和target矩阵是否相同,如果相同,就不需要进行后面的轮转了。
注意:因为题目说的是轮转若干次,所以不能忽略不轮转的情况,我们需要判断初始状态的mat和target是否相同。
代码
class Solution {
public:bool findRotation(vector<vector<int>> &mat, vector<vector<int>> &target) {int n = mat.size();vector<vector<int>> t(n, vector<int>(n));if (is_same(target,mat))return true;for (int i = 0; i < 3; ++i) {for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {t[j][n - 1 - i] = mat[i][j];}}if (is_same(target,t))return true;mat=t;}return false;}bool is_same(vector<vector<int>> &mat, vector<vector<int>> &target) {int n = mat.size();for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {if (mat[i][j] != target[i][j])return false;}}return true;}};



















