数据科学和机器学习统计 (STATISTICS FOR DATA SCIENCE AND MACHINE LEARNING)

Categorical variables are the ones where the possible values are provided as a set of options, it can be pre-defined or open. An example can be the gender of a person. In the case of Ordinal variables, the options can be ordered by some rule, like the Likert Scale:

分类变量是将可能的值作为一组选项提供的变量，可以预定义或打开。 一个例子可以是一个人的性别。 对于序数变量，可以按照某些规则对选项进行排序，例如Likert Scale：

• Like
  喜欢
• Like Somewhat
  有点像
• Neutral
  中性
• Dislike Somewhat
  有点不喜欢
• Dislike
  不喜欢

To simplify further examples, we will use a simple example, based on a group of students that have passed or not 2 distinct exams, the results are represented in the next RxC table:

为了简化更多示例，我们将使用一个简单示例，该示例基于一组已通过或未通过2次不同考试的学生，结果显示在下一个RxC表中：

Statisticians have developed specific techniques to analyze this data, the most important are:

统计人员已经开发出分析此数据的特定技术，其中最重要的是：

协议措施 (Measures of Agreement)

百分比协议 (Percent Agreement)

Calculated as the divisions between the number of cases where the rates are in a certain class by the total number of rates.

计算为费率在特定类别中的案例数除以费率总数。

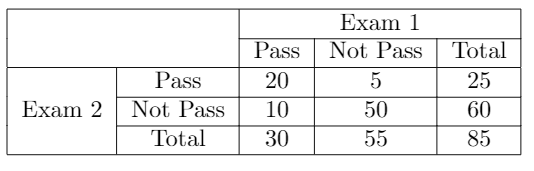
• The percent agreement for Passing the exam 2 is 25/(25+60) = 0.29, so 29.4%
  通过考试2的百分比协议是25 /(25 + 60)= 0.29，所以29.4％
• The percent agreement for Passing the exam 1 is 30/85 = 0.35, so 35.3%
  通过考试1的百分比协议是30/85 = 0.35，所以35.3％
• The percent agreement of passing the exam 1 and not passing the exam 2 is 10/85 = 0.117, so 11.7%.
  通过考试1和未通过考试2的百分比协议是10/85 = 0.117，所以11.7％。

The problem with the percent agreement is that the data can be obtained only by chance.

百分比一致性的问题在于只能偶然获得数据。

科恩的卡帕 (Cohen’s Kappa)

To overcome the problems of percent agreement, we calculate Kappa as:

为了克服百分比协议的问题，我们将Kappa计算为：

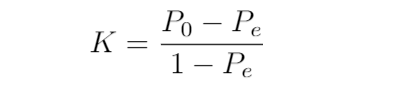
where P0 is the observed agreement and Pe the expected agreement, calculated as:

其中P0是观察到的协议， Pe是期望的协议，计算公式为：

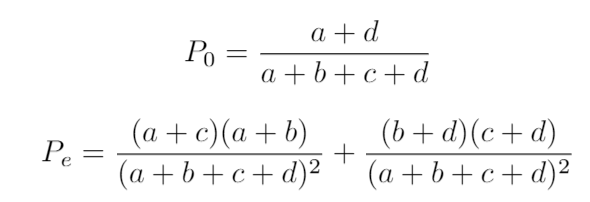
In our example:

在我们的示例中：

• P0 = 70/85 = 0.82

  P0 = 70/85 = 0.82

• Pe = 30 x 25 / 85² + 55 x 60 / 85² = 0.56

  Pe = 30 x 25 /85²+ 55 x 60 /85²= 0.56

• K = 0.26 / 0.44 = 0.59

  K = 0.26 / 0.44 = 0.59

The Kappa results are in possible range is (-1,1), where 0 means that observed agreement and chance agreement is the same, 1 if all cases were in agreement and -1 if all cases were in disagreement.

Kappa结果的可能范围是(-1,1)，其中0表示观察到的一致和机会一致是相同的，如果所有情况都一致，则为1；如果所有情况都不一致，则为-1。

卡方分布 (The Chi-Squared Distribution)

To do hypothesis testing with categorical variables, we need to use custom distributions, the most common is the Chi-Square, being a continuous theoretical probability distribution.

要使用分类变量进行假设检验，我们需要使用自定义分布，最常见的是卡方，即连续的理论概率分布。

This distribution has only one parameter, k which means degrees of freedom. As k approaches infinity, the chi-Squared distribution becomes similar to the normal distribution.

这种分布只有一个参数， k表示自由度。 当k接近无穷大时，卡方分布变得类似于正态分布。

卡方检验 (Chi-Squared Test)

This test is used to check if two categorical variables are independent, we will use the same example to explain how to calculate it:

该测试用于检查两个类别变量是否独立，我们将使用相同的示例来说明如何计算它：

First, we define the hypothesis that we want to test, in our case, we want to check if passing exam 1 and exam 2 are independent, so:

首先，我们定义要测试的假设，在本例中，我们要检查通过考试1和考试2是否独立，因此：

• H0 = Pass exam 1 and pass exam 2 are independent.
  H0 =通过考试1和通过考试2是独立的。
• Ha = Pass exam 1 and pass exam 2 are dependent.
  Ha =通过考试1和通过考试2是相关的。

This test relies on the difference between expected and observed values, to calculate the expected values(what you expect to find if both variables were independent), we use:

该测试依赖于期望值与观察值之间的差异，以计算期望值(如果两个变量都是独立的，您会发现什么)，我们使用：

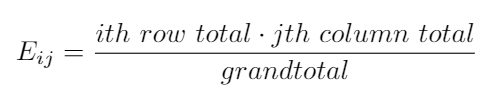
To simplify the calculations first we calculate the marginals, these values are the sums per row and column that we already calculated in the second table if this post. The expected values are calculated as:

为了简化计算，首先我们计算边际，这些值是我们在第二张表中已经计算出的每行和每列的总和。 期望值的计算公式为：

Now we have all we need to calculate the chi-squared formula:

现在我们有了计算卡方公式所需的全部：

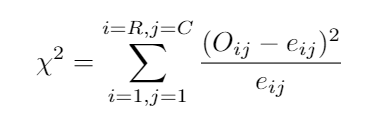
With the sum symbol, we mean that we have to calculate the formula for all combinations of our variables, in our case 4, and sum the results:

对于总和符号，我们的意思是我们必须为变量4的所有组合计算公式，并对结果求和：

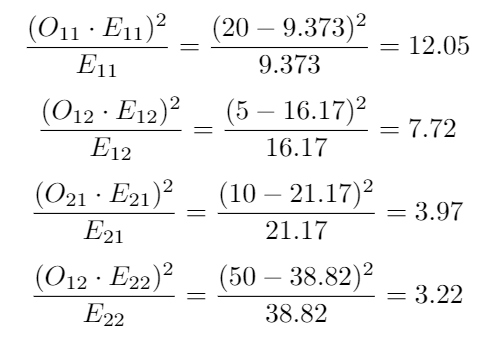
The final values are the sum of all 4, being 26.96, now we have to compare this result with the statistical tables, for this we need to know the degrees of freedom, they are calculated as (num rows-1)*(num columns-1), in our case we have a degree of freedom = 1.

最终值是所有4的总和，即26.96 ，现在我们必须将此结果与统计表进行比较，为此，我们需要知道自由度，它们的计算方式为(num rows-1)*(num columns -1) ，在我们的情况下，我们的自由度= 1。

According to the tables found easy searching Chi-Squared table at Google(statistical packages for any language should have them in a function), the critical value for 𝝰 = 0.05, is 3.841, our result is much larger, so, we reject the null hypothesis which means that pass exam 1 and pass exam 2 are dependent.

根据在Google上发现的易于搜索的Chi-Squared表(任何语言的统计软件包都应在函数中包含它们)，, = 0.05的临界值为3.841，我们的结果要大得多，因此，我们拒绝空值假设意味着通过考试1和通过考试2是相互依赖的。

分类数据的相关统计 (Correlation statistics for categorical data)

As person correlation requires variables to be measured on at least interval level, we need to adopt a new calculation for binary and ordinal variables, let’s introduce them:

由于人的相关性要求至少在区间水平上测量变量，因此我们需要对二进制和序数变量采用新的计算方法，让我们对其进行介绍：

二进制变量 (Binary Variables)

Phi is a measure of the degree of association between two binary variables, based on the table introduced at the Cohen’s Kappa sections, it’s calculated as:

Phi是两个二进制变量之间关联度的度量，基于Cohen Kappa部分介绍的表，其计算公式为：

Using the second formula, in our example, Φ = (26.96/85)^(1/2) = 0.1

在我们的示例中，使用第二个公式，Φ=( 26.96 / 85)^(1/2)= 0.1

Notice that the first formula can obtain negative values, meanwhile, the second one can only result in positive values, we don't care about the direction of our result, we just analyze the absolute value.

注意，第一个公式可以得出负值，而第二个公式只能得出正值，我们不在乎结果的方向，我们只分析绝对值。

If the distribution of the data is 50–50, so data is evenly distributed, phi can reach the value of 1, else the potential max value is lower. In our case, we have very little relationship.

如果数据的分布是50–50，则数据分布均匀，phi可以达到1的值，否则潜在的最大值较低。 就我们而言，我们之间的关系很少。

点-双相关 (The Point-Biserial Correlation)

It’s a measure that calculates the correlation between dichotomous and continuous variables, the formula is the next-one:

这是一种计算二分变量和连续变量之间的相关性的度量，公式为下一个：

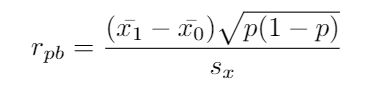
Where:

哪里：

• x̄1 = mean of the continuous variable for group 1

  x̄1 =组1连续变量的平均值

• x̄2 = mean of the continuous variable for group 2

  x̄2 =第2组连续变量的平均值

• p = proportion of class 1 in the dichotomous variable

  p = 1类在二分变量中的比例

• s_x = Standart deviation of the continuous variable

  s_x =连续变量的标准偏差

To follow our example we will suppose the next values, obtained comparing the exam 1 variable with the number of hours studied:

遵循我们的示例，我们将假定下一个值，该值是将考试1变量与学习的小时数进行比较而获得的：

• x̄ pass = 5.5

  x̄通过 = 5.5

• x̄ not pass = 3.1

  x̄不及格 = 3.1

• p = 20/25 = 0.8

  p = 20/25 = 0.8

• s_x = 2

  s_x = 2

With these values, we obtain a result of 2.4 * 0.4 / 2 = 0.48, indicating that there’s some relation between our variables.

使用这些值，我们得到的结果为2.4 * 0.4 / 2 = 0.48 ，表明变量之间存在某种关系。

序数变数 (Ordinal Variables)

The most used correlation coefficient for ordinal variables is the Spearman’s rank-order coefficient, usually called Spearman’s r.

序数变量最常用的相关系数是Spearman的秩序系数 ，通常称为Spearman的r 。

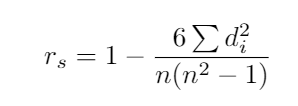
where d_i means the difference between 2 variables for each individual and n the size of the sample.

其中d_i表示每个个体的2个变量与样本大小的n之差。

摘要 (Summary)

In data science, we’re used to do some scatter plots of the binary, categorical or ordinary variables, use them as color differences in other plots, but when we calculate the correlations it’s easy to skip this variable, because of the built-in functions for pandas in the case of python or Dplyr in R don't use them.

在数据科学中，我们习惯于对二进制，分类或普通变量进行散点图绘制，将它们用作其他图中的色差，但是当我们计算相关性时，由于内置变量，很容易跳过此变量R中的python或Dplyr的熊猫函数不使用它们。

In this post, we showed how to analyze these variables' distribution and their correlation with all the other variables.

在这篇文章中，我们展示了如何分析这些变量的分布以及它们与所有其他变量的相关性。

This is the tenth post of my particular #100daysofML, I will be publishing the advances of this challenge at GitHub, Twitter, and Medium (Adrià Serra).

这是我特别＃十后100daysofML，我会发布在GitHub上，Twitter和中型企业(这一挑战的进步阿德里亚塞拉 )。

https://twitter.com/CrunchyML

https://twitter.com/CrunchyML

https://github.com/CrunchyPistacho/100DaysOfML

https://github.com/CrunchyPistacho/100DaysOfML