In FAANG company interview, Candidates always come across heap problems. There is one question they do like to ask — Top K. Because these companies have a huge dataset and they can’t always go through all the data. Finding tope data is always a good option. In this article, I would like to share my methodology on handling heap interview problems. Also, I’ll share 2 typical heap algorithm problems — Top K Frequent, Merge K arrays.

在FAANG公司面试中，候选人总是遇到堆砌问题。 他们想问一个问题-TopK。因为这些公司拥有庞大的数据集，而且不能总是遍历所有数据。 查找tope数据始终是一个不错的选择。 在本文中，我想分享我的方法来处理堆访谈问题。 另外，我将分享2个典型的堆算法问题-排在前K个，合并K个数组。

什么是堆？ (What is Heap?)

Heap is a complete Tree-like data structure. It has a parent node, left child node and right child node. For the interview, the min-heap and max-heap are very common to see.

堆是一个完整的树状数据结构。 它具有父节点，左子节点和右子节点。 对于采访来说，最小堆和最大堆很常见。

Max-Heap: In a Max-Heap the value present at the parent node must be greatest among the values present at all of its children.

最大堆 ：在最大堆中，父节点上存在的值必须在其所有子节点上存在的值中最大。

Min-Heap: In a Min-Heap the value present at the parent node must be minimum among the values present at all of its children.

最小堆 ：在最小堆中，父节点上存在的值必须在其所有子节点上存在的值中最小。

堆方法 (Heap methodology)

This is the methodology to help think about the solution:

这是帮助考虑解决方案的方法：

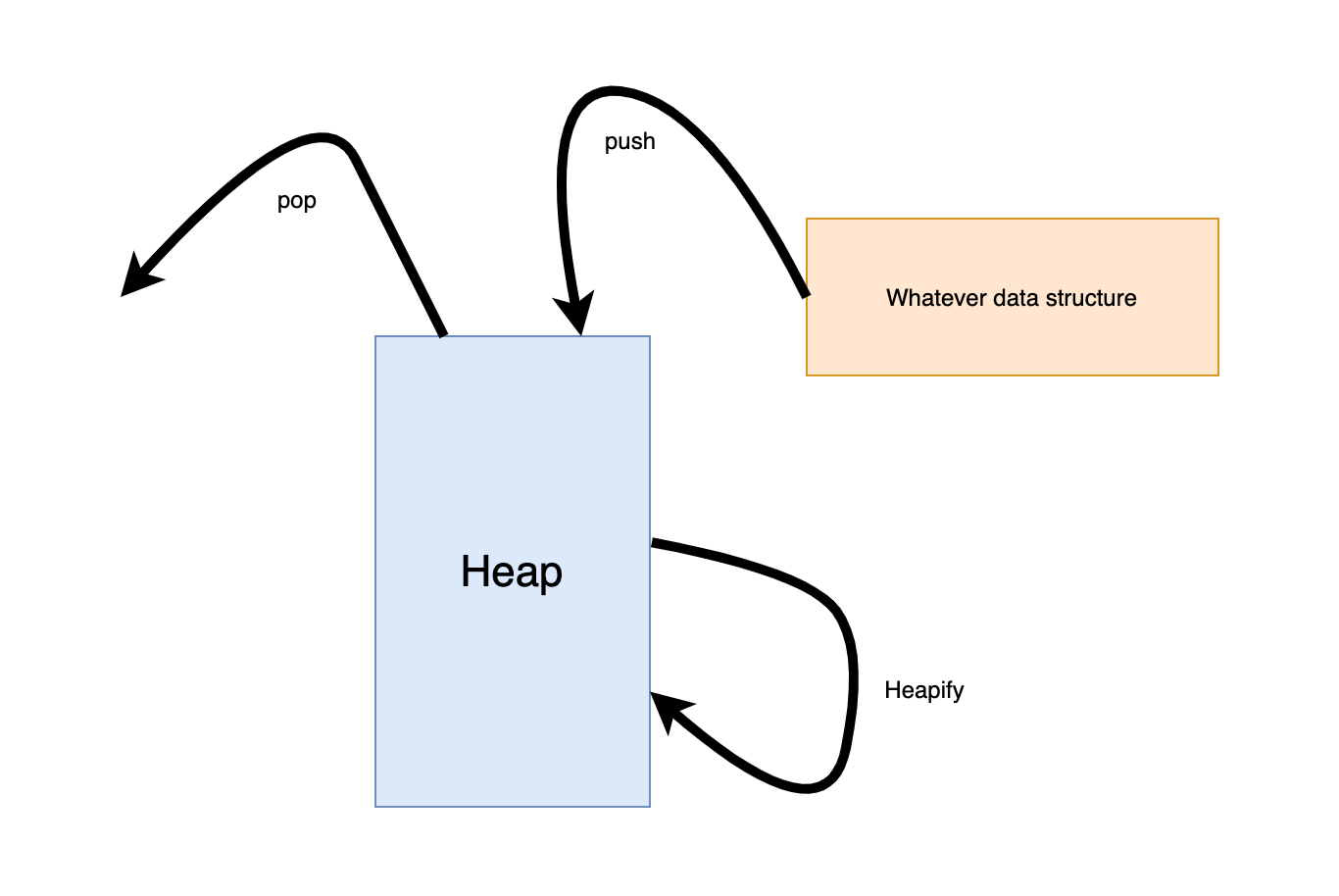
For most of the popular data structure problems. The feature is common: we have to do sort-like steps. We can sort all the elements: heapsort. We can sort just several elements: top-k. The elements should be comparable. Otherwise, we may have to push some comparable value along with the elements.

对于大多数流行的数据结构问题。 该功能很常见：我们必须执行类似排序的步骤。 我们可以对所有元素进行排序：heapsort。 我们可以对几个元素进行排序：top-k。 元素应该是可比较的。 否则，我们可能不得不将一些可比较的价值与要素一起推向市场。

Push: What we push some comparable elements such as int. Sometimes I have to push a comparable object. No matter what we push, we are doing it for comparison and heapify.

推送 ：我们推送一些可比较的元素，例如int。 有时我必须推动一个类似的对象。 无论我们推动什么，我们都在进行比较和堆化。

Heapify: Heapify is the process of converting a binary tree into a Heap data structure by rearranging the nodes in the binary tree to a max-heap or min-heap.

Heapify ：Heapify是通过将二叉树中的节点重新排列为max-heap或min-heap来将二叉树转换为Heap数据结构的过程。

In case one of your interview questions is implementing heapify, Here I attached the code:

如果您的面试问题之一是实现heapify，请在此处附加代码：

In this case, we have to push the node to the heap. As heap’s representation is an array. It appends the new node to the end and heapify it. Here is the code for a max-heap:

在这种情况下，我们必须将节点推送到堆。 由于堆的表示是一个数组。 它将新节点附加到末尾并对其进行堆放。 这是最大堆的代码：

For each insert, it takes O (log K) time to heapify the node, K is the heap size.

对于每个插入，需要O(log K)时间来堆满节点，K是堆大小。

Pop: Now it’s time to get what we want. Here we have two cases:

Pop ：现在是时候获得我们想要的东西了。 这里有两种情况：

• We use the value on the root of the heap. If needed, we can use heap[0] to check the top one if we have some extra conditions in the question. After we get the value, we can put it in an array or do extra work as the question requested.

  我们在堆的根上使用该值。 如果需要，可以在问题中使用一些额外的条件，使用heap [0]检查最上面的一个。 获得值后，我们可以将其放入数组中，也可以根据要求进行其他工作。

• In other cases, we need the rest of the values in the Heap. We can loop through the heap and return it.
  在其他情况下，我们需要堆中的其余值。 我们可以遍历堆并返回它。

实践 (Practices)

Here I provide solutions with python. For most of the Algorithm problems, it’s not just one solution. It’s better to give different solutions, analyse the time/space complexity and move to the best one.

在这里，我提供了python解决方案。 对于大多数算法问题，这不仅仅是一种解决方案。 最好提供不同的解决方案，分析时间/空间的复杂性，然后转向最佳解决方案。

In python, we have heapq library to help us operate the heap properly. It has nlargest and nsmallest which we can use to solve top-k type problem in one line of code. However, to ensure you can understand better about Heap, let’s go step by step.

在python中，我们有heapq库来帮助我们正确地操作堆。 它具有nlarge和nsmallest ，可用于在一行代码中解决top-k类型的问题。 但是，为了确保您可以更好地了解Heap，让我们逐步进行。

前K频 (Top K Frequent)

Here is the reference question on leetcode. We just find the top K frequent values in an array.

这是有关leetcode的参考问题 。 我们只是在数组中找到前K个频繁值。

Here are the steps from the code:

这是代码中的步骤：

• Convert the array to a new array where the element is a tuple with value and frequency.
  将数组转换为新数组，其中元素是具有值和频率的元组。
• Push the tuple elements to the k-size heap. The heap heapify automatically whenever a new node has been pushed.
  将元组元素推入k大小的堆。 每当推送新节点时，堆都会自动堆化。
• After we go through all the elements with the heap, we loop the rest of the heap to find our target values.
  在遍历了堆中的所有元素之后，我们循环其余堆以找到目标值。

If you are pushing an object, you have to ensure the object is comparable. If you push a tuple, the heap compare the first element while doing heapify, if ties happened, it will compare the next value.

如果要推动对象，则必须确保该对象具有可比性。 如果推入一个元组，堆将在执行heapify时比较第一个元素，如果发生联系，它将比较下一个值。

合并K个数组 (Merge K arrays)

Here is the reference question on leetcode. We have to Merge k sorted linked lists and return it as one sorted list. Here is the solution with Heap:

这是有关leetcode的参考问题 。 我们必须合并k个排序的链表，并将其作为一个排序表返回。 这是堆的解决方案：

Here are the steps from the code:

这是代码中的步骤：

• We build an array with the first node and its value from each ListNode in lists. Then we heapify it to be a min-heap.
  我们使用列表中每个ListNode的第一个节点及其值构建一个数组。 然后我们将其堆成最小堆。
• We use the peek node in the heap to build the output ListNode.
  我们使用堆中的peek节点构建输出ListNode。

• If the node not ends, we use heapreplace which means we pop and return the smallest item from the heap, and also push the new item.

  如果节点未结束，则使用heapreplace，这意味着我们从堆中弹出并返回最小的项，并推送新项 。

Here I would like to explain another solution to this question with the Priority Queue.

在这里，我想用“优先级队列”解释这个问题的另一种解决方案。

Priority Queues are abstract data structures where each data/value in the queue has a certain priority. Priority Queue is an extension of the queue with the following properties.1, An element with high priority is dequeued before an element with low priority.2, If two elements have the same priority, they are served according to their order in the queue.

优先级队列是抽象的数据结构，其中队列中的每个数据/值都有特定的优先级。 Priority Queue是具有以下属性的队列的扩展：1，将高优先级的元素排在优先级低的元素之前。2，如果两个元素具有相同的优先级，则根据它们在队列中的顺序进行服务。

Here are the steps from the code:

这是代码中的步骤：

• From each element in the List, we find the first node with its value in the ListNode, put it into the Priority Queue. We need the node value because we need it for comparison in the Priority Queue.
  从List中的每个元素中，我们在ListNode中找到具有其值的第一个节点，并将其放入Priority Queue。 我们需要节点值，因为在优先级队列中需要进行比较。
• Then, we get the element from the Priority Queue (the element with the smallest value), link it to the output ListNode.
  然后，我们从Priority Queue中获得元素(值最小的元素)，并将其链接到输出ListNode。
• We move the node to the next, if it exists, we put it into the Priority Queue. After all these steps, we return the output ListNode which is the head.next.
  我们将节点移到下一个节点(如果存在)，将其放入优先级队列。 完成所有这些步骤之后，我们返回输出ListNode，它是head.next。

最后的话 (Final Words)

After you read this article, you may think heap is not as hard as you thought with this methodology. However, we may have other data structure comes up with Heap such as the LinkedList. Therefore, we still need to practise and master the basic data structure API with the language you preferred.

阅读本文之后，您可能会认为堆并不像您对这种方法所想象的那样难。 但是，Heap可能还会提供其他数据结构，例如LinkedList。 因此，我们仍然需要使用您喜欢的语言来练习和掌握基本的数据结构API。

Hope you learn something from this article. If you are interested in reading any of my other articles, you are welcome to check them out in my profile. Best wishes for your job hunting!

希望您能从本文中学到一些东西。 如果您有兴趣阅读我的其他文章，欢迎您在我的个人资料中查看。 祝您工作愉快！