使用了Matlab代码,化简平时遇到的计算问题,也可以用于验算结果
来自211工科专业2学分复变函数与积分变换课程
求复角主值
sym(angle(待求复数))%公式
sym(angle(1+sqrt(3)*i))%举例代入化简
将
syms f z
f=1/(z*(z+1));%某一函数f(z)
f=subs(f,z,1/z);%可以把1/z换成任意关系式
f=simplify(f/(z^2));一维积分计算
简单的积分计算,matlab中不加;即可显示符号型变量,使用double()函数可以转化为数值型显示。
syms x z(x) %定义关于x的函数z
u=@(x)3*(i*x^2-x^2);%某函数
jf1=int(u,x,[0,i]);%这里可以是定积分、不定积分、变上限积分,只需要在[]内更改
jf1%符号型显示
double(jf1)%数值型显示级数求和
用于计算级数是否收敛、条件收敛、绝对收敛。对目标级数s(n)判断是否收敛直接使用symsum()级数求和函数,如果需要判断是否绝对收敛时使用abs()函数取模即可。
syms s n
s=@(n)(8^n)/factorial(n);%factorial()阶乘函数
s=@(n)abs(((-1)^n)/n);
qh=symsum(s,n,1,inf)
double(qh)二次积分
连续计算两次积分的基础计算,详细见「概率论」部分
低薪小明:「概率论」基础计算代码zhuanlan.zhihu.com
syms x y z(x,y)
u=@(x,y)6-x-y;
jf1=int(u,y,[2,3-x]);
jf2=int(jf1,x,[0,1]);
%jf=int(z,x,[0,inf]);
jf1
jf2
%double(jf)一阶、二阶微分计算
经典题型:由u(x,y)构造解析函数f(z),首先对u相应的求导,然后由于解析函数的性质对v积分,最终化简得到f(z).
clc
syms x y u
u=@(x,y)x^2-y^2+x*y;
ux=diff(u,x)%u对x求导
uy=diff(u,y)%u对y求导
vx=diff(u,x,2)
vy=diff(u,y,2)
vjfy=int(ux,y)
vx=diff(vjfy,x)普通求导并代入计算
结合高阶求导公式计算结果,先求导,再将相应的z0代入求值,非常简便。
syms f z
f=1/sin(z);
df=diff(f,z)
subs(df,z,0)普通极限
显而易见,这用来求一个函数的极限
- 用于判断极限是否存在
- 判断是否收敛
- 判断奇点类型
- 求留数
- 等等
syms f n
f=@(n)(1+1/n)^n;
limit(f,n,inf)%这里也可以计算在某一点的极限,不一定是无穷∞三角极限
用于含三角函数的留数计算,不常用
syms f z
for k=0:1:10f=@(z)(z-k*pi)/sin(z);limit(f,z,k*pi)
end对圆积分
在圆上的积分,用于第三章、第五章的积分计算,不过使用柯西积分公式、高阶求导公式或留数公式等等也能算出。
syms seita
u=@(seita)exp(seita.*j);%圆的指数是方程
f=@(seita)exp(-1*j*seita);%被积函数
I=int(f*diff(u,seita),seita,0,pi);保形映射公式计算
针对第六章知道几对映射点求保形映射后的点,只是简单的化简计算,在代码中输入初始点就行。
clc
syms z w(z);
w=(z+2)*i/(z-2);
w1=subs(w,z,0)
scatter(real(w1),imag(w1));
hold on
w2=subs(w,z,1)
scatter(real(w2),imag(w2));
hold on
w3=subs(w,z,-1)
scatter(real(w3),imag(w3));
hold on
w4=subs(w,z,-i)
scatter(real(w4),imag(w4));
hold on
%zuo=expand((w+i)/((w+3*i))*4)
%you=expand(z/(2*(z-1)))保形映射画图
针对第六章对复平面某一区域求保形映射后的区域,在第一行的x和y分别输入21个表示该区域边界的离散点,并在循环中输入映射函数,即可得到映射后图形。
不过这里有一个限制条件:初始区域只能是方形区域,对圆形区域或者三角区域无法处理,欢迎大家提出宝贵的改进意见。
x=-10:1:10;y=linspace(-pi,0,21);w=zeros(1,441);
for j=1:20for k=1:21w((j-1)*21+k)=exp(x(j)+y(k)*i);end
end
realw=real(w);
imagw=imag(w);
scatter(realw,imagw);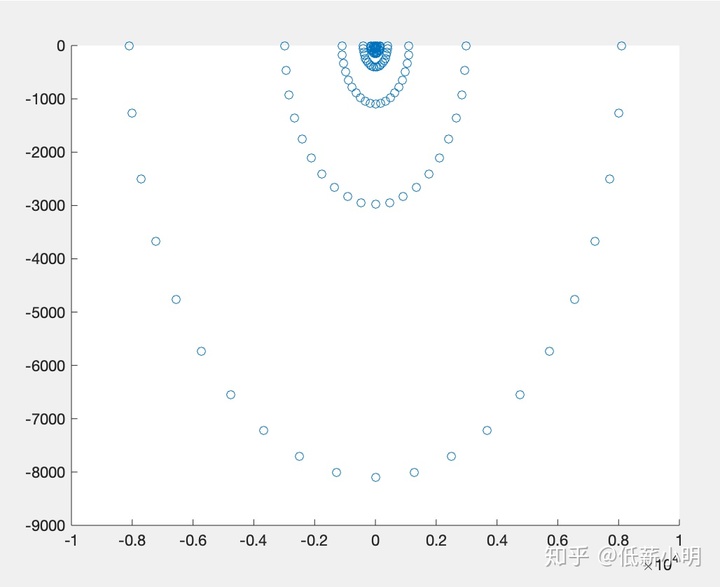

![[luoguP4142]洞穴遇险](http://pic.xiahunao.cn/[luoguP4142]洞穴遇险)

















