什么是ARIMA？ (What is ARIMA?)

ARIMA models are one of the most classic and most widely used statistical forecasting techniques when dealing with univariate time series. It basically uses the lag values and lagged forecast errors to predict the feature values.

ARIMA模型是处理单变量时间序列时最经典，使用最广泛的统计预测技术之一。 它基本上使用滞后值和滞后的预测误差来预测特征值。

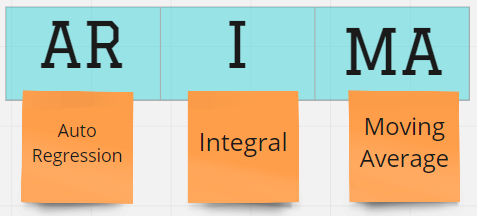
• AR: using the lags of previous values

  AR：使用先前值的滞后

• I: non-stationary differencing

  I： 非平稳差分

• MA: moving average for the error term

  MA： 移动平均线 对于错误项

Some of these terms are very commonly used when working with time-series data. ARIMA models can fit accurately if we deeply understand these terms or components of the data. Following are the few of them:

其中一些术语在处理时间序列数据时非常常用。 如果我们深刻理解数据的这些术语或组成部分，则ARIMA模型可以准确拟合。 以下是其中一些：

趋势： (Trend:)

Data is considered to have a trend when there is an increase or decrease direction in the data. E.g. increase of airline passengers during summer, reduction in a number of customers during weekdays, etc.

当数据中存在增加或减少的方向时，数据被认为具有趋势 。 例如，夏季航空乘客的增加，工作日乘客数量的减少等。

季节性： (Seasonality:)

Data is considered to have a seasonal pattern if the data is influenced by external factors. For instance, growth and fall of leaves are driven by the weather/season of mother nature.

如果数据受外部因素影响，则认为该数据具有季节性模式 。 例如，树叶的生长和下降是由自然的天气/季节驱动的。

循环性： (Cyclicity:)

Data is considered to have a cyclic component if there are repeated but non-periodic fluctuations. In simple words, if the pattern is caused because of certain circumstances and there is no set amount of time, it can be considered as cyclicity. For instance, the stock market exhibits cyclic behavior with highs and lows due to the occurrence of specific events and the time between such peaks is never precise.

如果出现重复但非周期性的波动，则认为数据具有循环成分 。 简而言之，如果模式是由于某些情况造成的，并且没有固定的时间量，则可以将其视为周期性。 例如，由于特定事件的发生，股票市场表现出周期性的高低波动，而这种高峰之间的时间从来都不是精确的。

白噪声： (White Noise:)

This is the random and irregular component of the time series. In other words, the residuals after extracting trend+seasonality+cyclicity from the signal are mostly considered as white noise. The best example of white noise is when you lost your antenna connection to TV in the 90s (yes I am a 90s kid!).

这是时间序列的随机和不规则部分。 换句话说，从信号中提取趋势+季节+周期性后的残差通常被认为是白噪声。 白噪声的最好例子是在90年代您失去与电视的天线连接(是的，我是90年代的孩子！)。

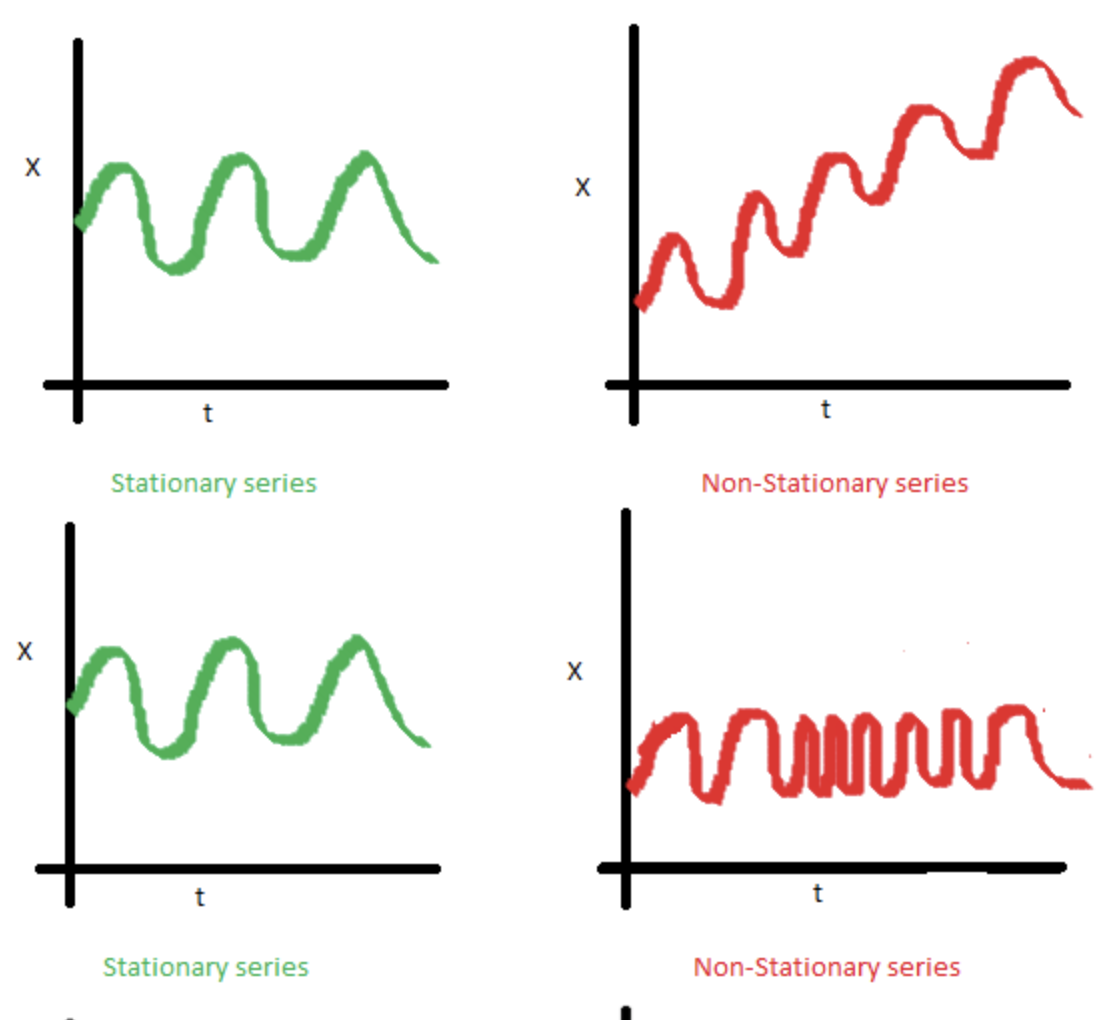
平稳性： (Stationarity:)

A time series with constant mean and zero variance is considered to be stationary. A well-known image that always strikes my mind when considering stationarity is:

具有恒定均值和零方差的时间序列被认为是平稳的 。 考虑平稳性时，我总是想起一个众所周知的图像：

The packages I have used to explain these tests mainly are:

我用来解释这些测试的软件包主要是：

• statsmodels: https://www.statsmodels.org/stable/index.html

  statsmodels ： https ： //www.statsmodels.org/stable/index.html

• pmdarima: http://alkaline-ml.com/pmdarima/index.html

  pmdarima ： http : //alkaline-ml.com/pmdarima/index.html

There are a lot of tests but I am going to talk about a few that I have used and helped me in my battle with time series problems:

有很多测试，但是我将讨论一些在时间序列问题上使用并帮助我的测试：

1.增强的Dickey-Fuller(ADF)测试： (1. Augmented Dickey-Fuller (ADF) test:)

Time series should be made stationary using transformation techniques (log, moving average, etc.) before applying ARIMA models. ADF test is a great way and one of the most widely used techniques to confirm if the series is stationary or not. The data can be found on Kaggle. Below is the code:

在应用ARIMA模型之前，应使用变换技术(对数，移动平均值等)使时间序列固定。 ADF测试是一种很好的方法，也是确认系列是否固定的最广泛使用的技术之一。 数据可以在Kaggle上找到。 下面是代码：

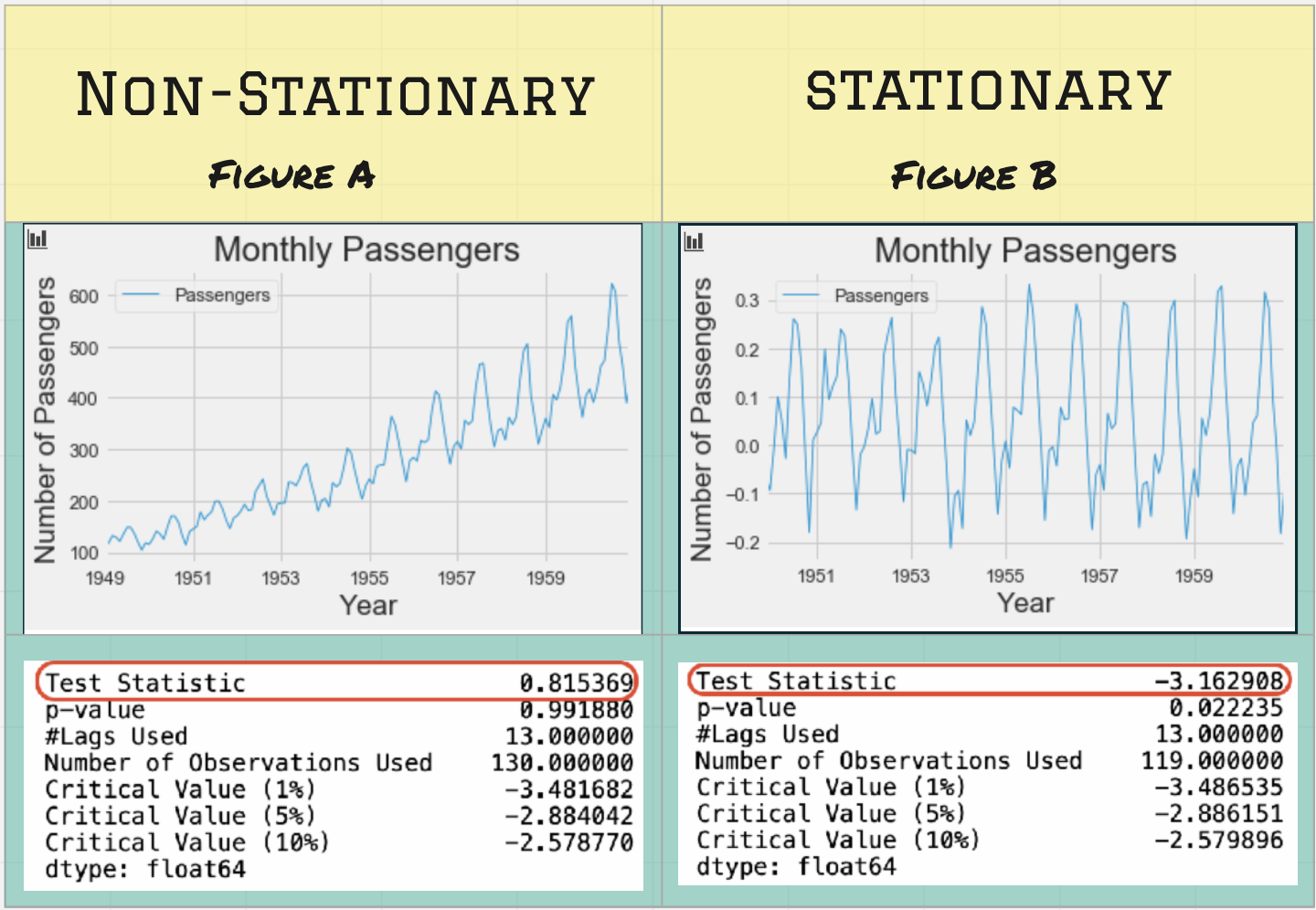
To make the data stationary we applied some transformation to the data (shown in code above). On calculating the t-statistic value we see that the value is significant and confirms that the data is stationary now!

为了使数据稳定，我们对数据进行了一些转换(如上面的代码所示)。 在计算t统计值时，我们看到该值显着，并确认数据现在处于静止状态！

2. PP测试： (2. PP test:)

PP stands for Phillips-Perron test. In some cases, I in ARIMA which stands for Integral is needed. Differencing of I=1 or 2 mostly does the job. This PP test is a unit root test to confirm that the time series is integrated of order 1. This is also an alternative to the ADF test if want to check stationarity. They have become quite popular in the analysis of financial time series[3]. Below is the code:

PP代表Phillips-Perron测试。 在某些情况下，需要ARIMA中代表Integral的I。 I = 1或2的差异大部分可以完成工作。 此PP测试是单位根测试，用于确认时间序列是否已集成1级。如果要检查平稳性，这也是ADF测试的替代方法。 在金融时间序列分析中，它们已经变得非常流行[3]。 下面是代码：

This will return a boolean value(1 or 0), indicating whether the series is stationary or not.

这将返回一个布尔值(1或0)，指示该序列是否平稳。

3. KPSS测试： (3. KPSS Test:)

A widely used test in econometrics is Kwiatkowski–Phillips–Schmidt–Shint or abbreviated as the KPSS test. This test is pretty similar to ADF too and can help to validate the null hypothesis that an observable time series is stationary around a deterministic trend. There is a major disadvantage though that it has a high rate of type-I errors. In such cases, it is often recommended to combine it with the ADF test and check if both of them return the same results[4]. The code is similar to the ADF test as shown below:

计量经济学中广泛使用的测试是Kwiatkowski–Phillips–Schmidt–Shint或简称为KPSS测试。 该测试也与ADF非常相似，并且可以帮助验证可观察的时间序列在确定性趋势附近平稳的零假设。 尽管存在很大的I型错误率，但它有一个主要缺点 。 在这种情况下，通常建议将其与ADF测试结合使用，并检查两者是否返回相同的结果[4]。 该代码类似于ADF测试，如下所示：

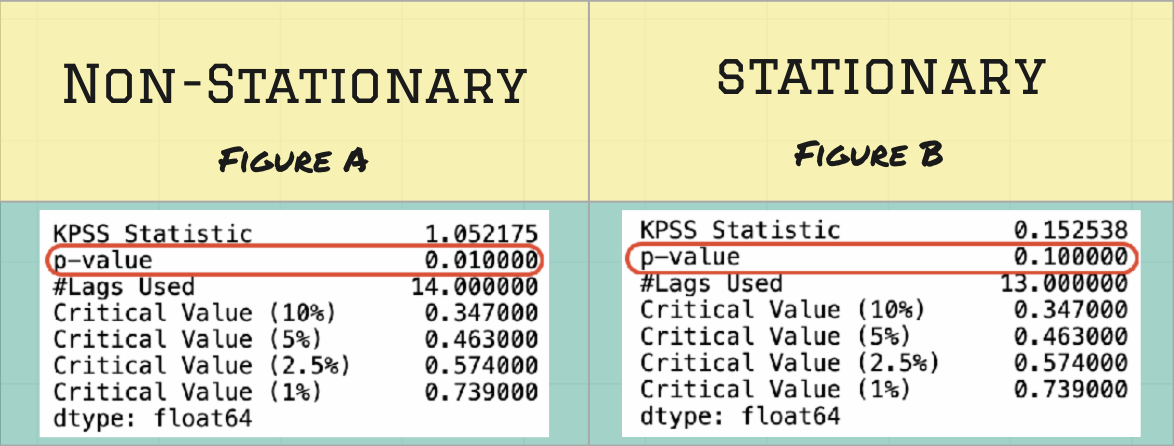
We can see from the image above that before applying the transformation(figure A) the p-value of data is <0.05 and thus it is not stationary. Post transformation(figure B) the p-value becomes 0.1 to. confirm the stationarity of the data.

从上图可以看出，在应用变换之前(图A)，数据的p值 <0.05 ，因此它不是平稳的。 转换后(图B)， p值变为0.1至。 确认数据的平稳性。

Before we dive into the next tests, it is important to know that ARIMA models may contain seasonal component that can be handled by adding a few more parameters(P, D, Q, m) to our ARIMA equation. We can broadly divide ARIMA type of models into two types:

在我们进行下一个测试之前，重要的是要知道ARIMA模型可能包含季节性分量 ，可以通过在ARIMA方程中添加更多参数(P，D，Q，m)来处理这些分量 。 我们可以将ARIMA类型的模型大致分为两种类型：

1. ARIMA: Handling Non-seasonal components as explained in the beginning

   ARIMA ：如开头所述处理非季节性组件

2. SARIMA: Seasonal Component + ARIMA

   SARIMA：S easonal组件 + ARIMA

4. CH测试： (4. CH Test:)

The Canova Hansen(CH) test is mainly used to test for seasonal differences and to validate that the null hypothesis that the seasonal pattern is stable over a sample period or it is changing across time. This is mostly helpful in economic or meteorological data[5]. This is already implemented in Python within pmdarima library.

Canova Hansen(CH)检验主要用于检验季节差异并验证零假设，即季节性模式在采样期内是稳定的或随时间而变化。 这对经济或气象数据最有帮助[5]。 这已经在pmdarima库中的Python中实现。

5. OCSB测试： (5. OCSB Test:)

Osborn, Chui, Smith, and Birchenhall (OCSB) test is used to determine if the data needs seasonal differencing (D component of P,D,Q,m). pmdarima package has a predefined function that one can leverage as follows:

Osborn，Chui，Smith和Birchenhall(OCSB)检验用于确定数据是否需要季节性差异(P，D，Q，m的D分量 )。 pmdarima软件包具有一项预定义的功能，可以按以下方式使用：

Here, we have defined m = 12 as it is monthly data. ‘aic’ is default lag_method for assessing performance(lower is better). Refer here for other accepted metrics. The output for this data is 1 as we already know that there is definitely visibility of the seasonal component.

在这里，我们将m = 12定义为月度数据。 “ aic”是用于评估效果的默认lag_method (越低越好)。 有关其他可接受的指标，请参考此处 。 该数据的输出为1，因为我们已经知道季节分量绝对可见。

6.分解图： (6. Decompose Plot:)

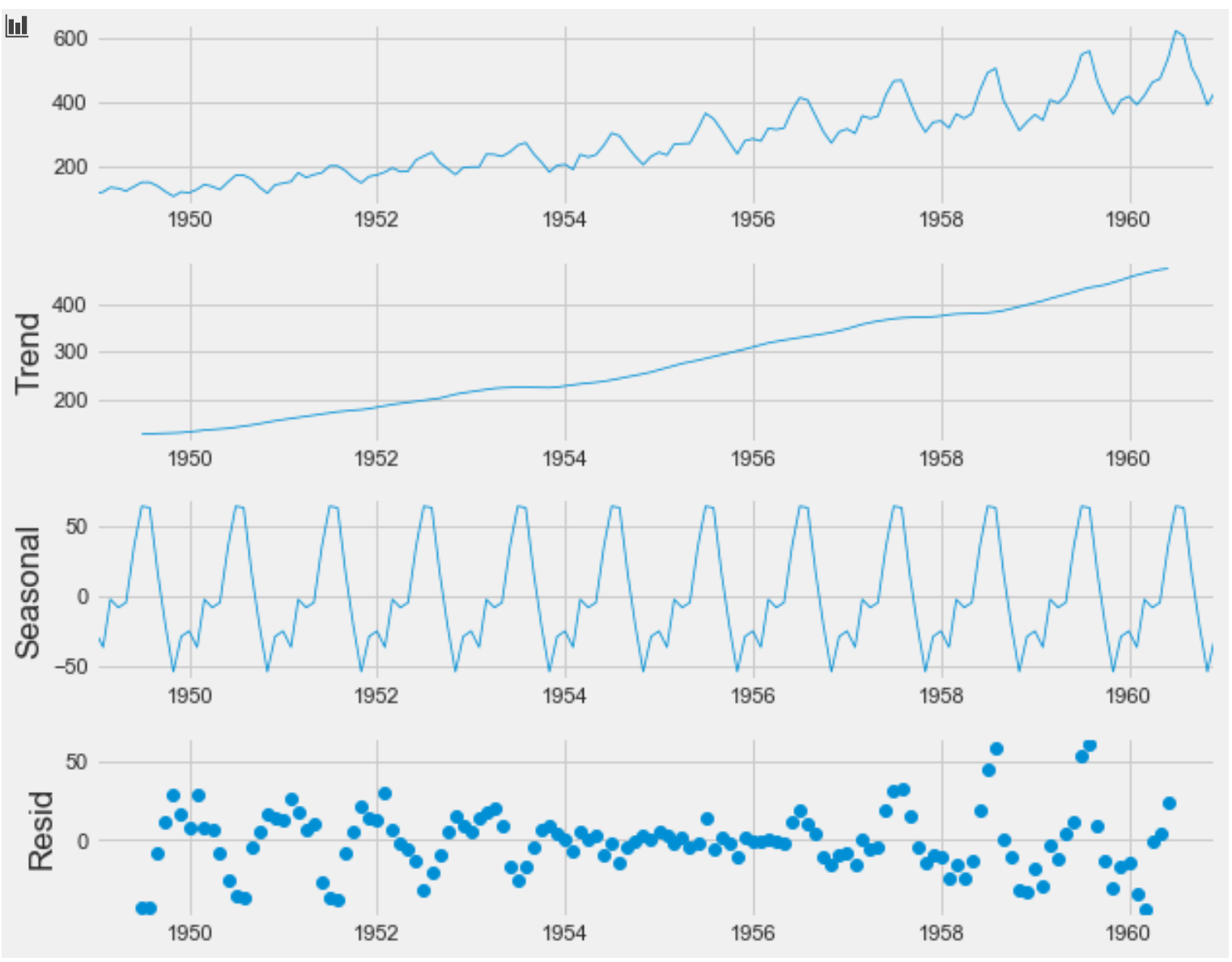
This is one of the tools that can really help when you encounter a time series problem. I think of this function is similar to the doctor taking vitals when you first go for a visit. As the vitals might indicate some obvious things in a patient, the decompose plot gives a breakdown of the data and shows if there are any clear trend, seasonality, and the pattern of residuals. Below is the snippet of the code and the output result:

这是遇到时间序列问题时真正有用的工具之一。 我认为此功能类似于您初次去看医生时要注意的重要事项。 由于生命体征可能指示患者中有一些明显的现象，因此分解图会分解数据并显示是否存在任何明确的趋势，季节性和残差模式。 下面是代码段和输出结果：

7. ACF和PACF图： (7. ACF and PACF Plot:)

ACF and PACF plot stand for Autocorrelation Plot and Partial Autocorrelation Plot respectively. ACF and PACF plot help to determine AR and MA terms needed in a systematic way after the time series has been stationarized. Below are the code for ACF and PACF plots:

ACF和PACF图分别代表自相关图和部分自相关图。 在时间序列平稳后，ACF和PACF图有助于系统地确定所需的AR和MA项。 以下是ACF和PACF图的代码：

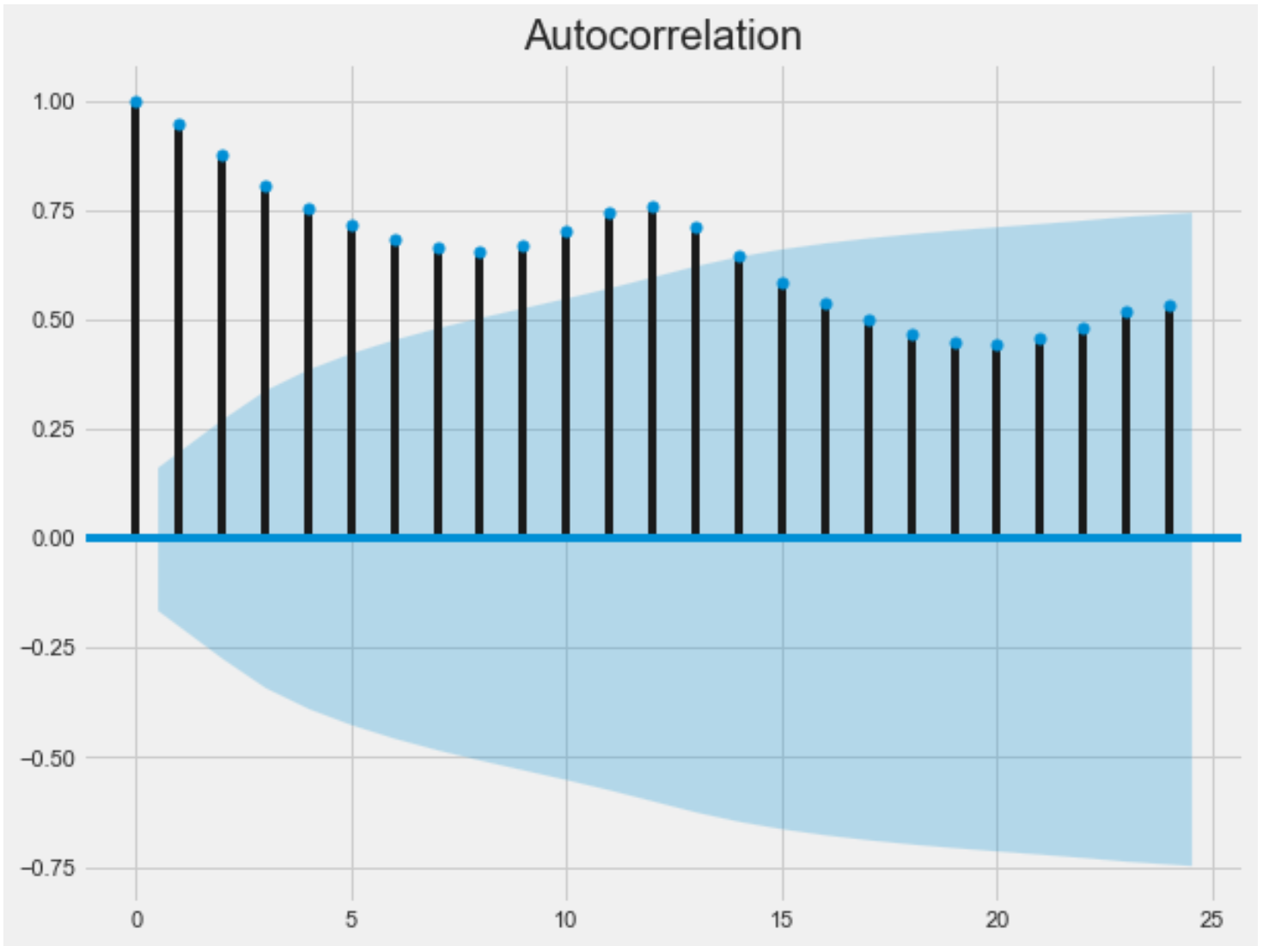
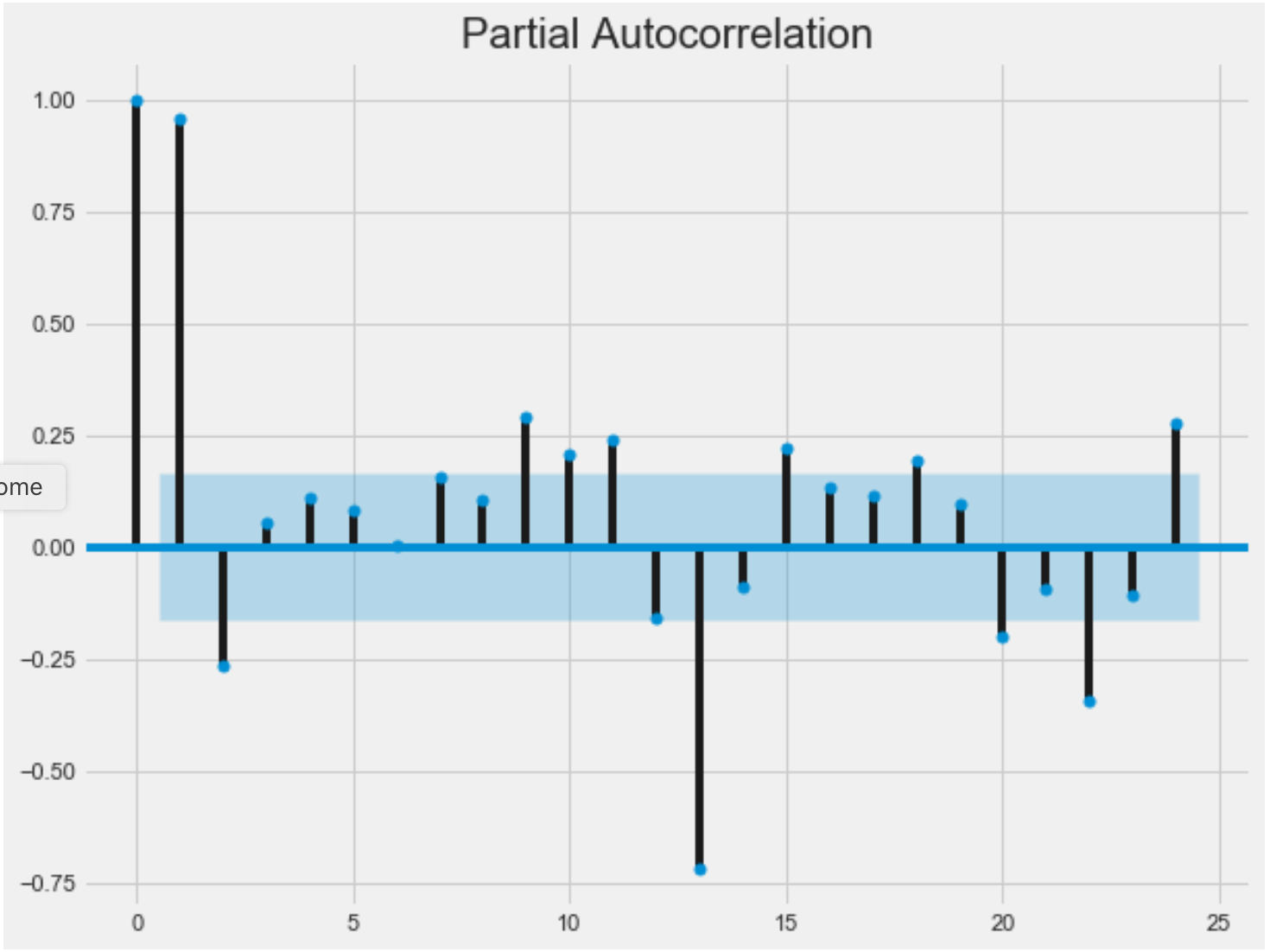
The lags which fall inside the blue shaded region are not considered to be significant. Based on the ACF plot we can say that it is AR13 model meaning AutoRegression with 13 lags would help. Based on the PACF plot we can say that it is MA2 model: Moving Average with 2 lags. There are methods to read these plots and have a good estimate of the order of the ARIMA model.

落在蓝色阴影区域内的滞后被认为不重要。 基于ACF图，我们可以说它是AR13模型，意味着具有13个滞后的自回归将有所帮助。 基于PACF图，我们可以说它是MA2模型： 2个滞后的移动平均线 。 有一些方法可以读取这些图并很好地估计ARIMA模型的阶数。

结论： (Conclusion:)

There are many other statistical tests that can be used other than listed above. However, the tests/tools I mentioned here can be really powerful to understand the data and fit accurate ARIMA models.

除上面列出的以外，还有许多其他统计测试可以使用。 但是，我在这里提到的测试/工具对于理解数据和拟合准确的ARIMA模型确实非常强大。

This is my first attempt to write an article on medium. I have learned a lot from my fellow writers and community and this is the best way I think to share or return some of my experiences back to them.

这是我在媒体上写文章的第一次尝试。 我从其他作家和社区中学到了很多东西，这是我认为与他人分享或回馈自己经验的最好方式。