基础概念公式推到可参考该专栏下的前几篇博文。
经山形组织图:
左半部分: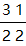 ,3上2下1上2下,右斜,飞数为+1
,3上2下1上2下,右斜,飞数为+1
右半部分: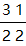 ,3上2下1上2下,左斜,飞数为-1
,3上2下1上2下,左斜,飞数为-1
左右两部分只有飞数是相反数,经纬纱组织点的运动规律保持不变。
一、求解二维矩阵的行列数即经纬纱循环数N1、N2
由经山组织图可观察得知:左半部分为左斜,飞数为+1;右半部分为右斜,飞数为-1。
严格意义上来讲,经山组织不属于规则组织,但是若从中间一分为二,左右两部分都为规则组织中的斜纹组织。
需要知道Kj,指明山峰的位置即可
行数的话,只需要将获取组织的一般形式的分子分母依次求和即可,即纬纱循环数N1=Σ(ci+di),i∈[1,m]。
列数的话,因为经山组织存在一个山峰,故是奇数列,其中以山峰Kj为划分,左半部分为Kj列(包含山峰所在列),右半部分为Kj - 2列,故其经纱循环数N2=2 × Kj - 2。
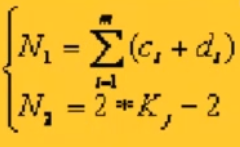
二、求第一列的元素值
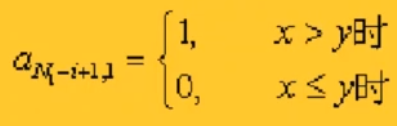 ,其中i=1,2,3…,N1。
,其中i=1,2,3…,N1。
三、左半部分——从第二列到Kj列,其飞数一直保持不变,可根据求规则组织的方法求解[2,Kj]列
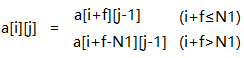 ,其中
,其中i=1,2,3...,N1;j=2,3,...,Kj
四、右半部分——求解Kj+1到N2列,其飞数也一直保持不变,但未原来飞数的负数,也可根据求规则组织的方法求解
通过公式可将负飞数转换为正数: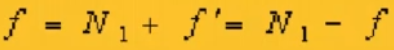
再跟2一样进行求解规则组织
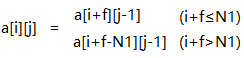 ,其中
,其中i=1,2,3...,N1;j=Kj + 1,...,N2
代码实现:
#include <iostream>
#include<stdio.h>
using namespace std;int main()
{int i,j,N1,N2,f,m,kj;//kj表示山峰的位置,从而确定出总列数N2int c[10],d[10],a[100][100];printf("please input m:");scanf("%d",&m);for(i=0;i<=m-1;i++){printf("please input C[%d]:",i+1);scanf("%d",&c[i]);printf("please input D[%d]:",i+1);scanf("%d",&d[i]);}printf("please input kj:");scanf("%d",&kj);//输入山峰位置,从而确定出总列数N1=0;//行数初始化,即纬纱循环数初始化,之后需要累加for(i=0;i<=m-1;i++){N1=N1+c[i]+d[i];}N2=2*kj-2;//总列数printf("please input f:");scanf("%d",&f);if(f<0)f=N1+f;//若飞数为负数,通过公式转换成正数/*
对第1列进行赋值
*/i=1;//先对第一列赋值,从第一列的第一行开始for(j=0;j<=m-1;j++){while(c[j]>0){a[N1-i+1][1]=1;//因为是分子,所有值都赋值为1c[j]--;i++;}while(d[j]>0){a[N1-i+1][1]=0;//因为是分母,所有值都赋值为0d[j]--;i++;}}/*
对2到kj列 进行赋值
*/for(j=2;j<=kj;j++){for(i=1;i<=N1;i++){if((i+f)>N1) a[i][j] = a[i+f-N1][j-1];else a[i][j]=a[i+f][j-1];}}f=N1-f;//求kj列到N2列右半部分的飞数需要将负值转变为正数/*
对kj列到N2列 进行赋值
*/for(j=kj+1;j<=N2;j++){for(i=1;i<=N1;i++){if((i+f)>N1) a[i][j] = a[i+f-N1][j-1];else a[i][j]=a[i+f][j-1];}}/*
输出二维数组a[i][j]
*/for(i=1;i<=N1;i++){for(j=1;j<=N2;j++){printf("%5d",a[i][j]);}printf("\n");}getchar();return 0;
}运行效果如下: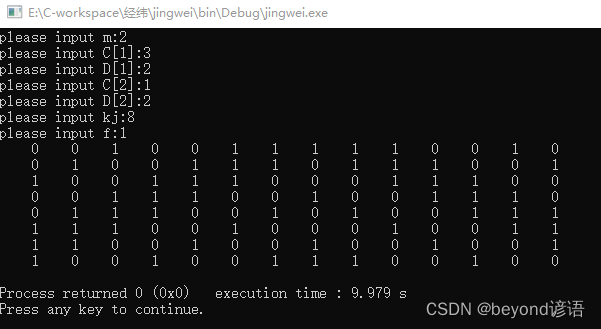
函数以及C ++中的示例)
)













![[Object-oriented] : 控制反转](http://pic.xiahunao.cn/[Object-oriented] : 控制反转)


![e-r模型教案高中计算机,《ER模型1》[数据库][计算机]教案.doc](http://pic.xiahunao.cn/e-r模型教案高中计算机,《ER模型1》[数据库][计算机]教案.doc)
利用ASP.NET加密和解密Web.config中连接字符串)