1. probability space 概率空间

1.1 概率基础

1.2 概率空间

2. Filtration

filtration在钱敏平老师和龚光鲁老师的《随机过程论》中直接称其为非降的KaTeX parse error: Undefined control sequence: \sigmma at position 1: \̲s̲i̲g̲m̲m̲a̲代数族。如图。

一般叫$\sigma$-代数流或$\sigma$-域流

在鞅论中的花体$F_t$，即filtration中文翻译成“滤波”或“滤子”，它在本质上是一个非降子$\sigma$-代数。这个名词的最早来源不是很清楚（有人说是从描述股票的价格变化过程中来的）。有时也把鞅论中(Ω,F,P,∪F_t)称为“被滤过的概率空间”。

这个概念是很抽象很拓扑的。看到这个filtration第一感觉就是滤子，因为它附带着一个序关系。

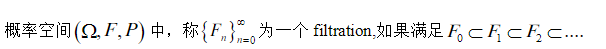
这是我搜集到的资料。看到这个概念的时候我就发现，啊，和我的生活好像啊。

下面解释一下我作为一个初学者的理解。

概率空间里的F是一个可测集类。一个集合就是一个事件，那么可测集类就表示『我们用现有的方法能够形成一个看待的事件』之总和。

比如我现在觉得国际政治很扯，当学霸性价比挺低。对我来说这两个例子是几乎不可能翻盘的，这样在阐述问题时比较方便。那么就相当于：
学霸→性价比低。
国际政治→很扯淡。
对这两件事我就能形成一个看待。但现在我对有些事情还没法形成一个看待，譬如：《随机过程》对我来说难吗？可能是难，可能是不难。
对于给定时刻，每一座城市都有权力寻租吗？可能是肯定，也可能是否定。
如果政治家有极强的同理心，对我们来说是好事吗？可能是，可能不是。那么就相当于：

• 《随机过程》→难，易
• 没有权力寻租的城市→存在，
• 不存在强同理心政治家→好，坏传统意义上

对以上三件我们无法确定的事，我们视为随机变量并按照主观or经验or等分性来赋予其取两个值的概率。这种赋予是不准确的，只有当我们必须要做出相关决策的时候，才不得不赋予一个。

但我们知道，有不可测集合。不是所有集合都能被定义一个合适的概率。（实变函数中的Vitali定理：实数上测度不为0的集合各自有个不可测子集）

所以我们就反过来想：既然以上三件事我们无法确定，那就干脆踹到可测集类F的外面去。我们不管它们，暂时也不做关于它们的决策。毕竟决策通常不是非做不可，搁置也是一种选择。

世界是好还是坏，是正义还是邪恶？我拒绝给出一个理性的回答，因为这件事我们无法确定。
世界上有百分之多少的事情呢？有的事情，比如开车，可以被视为一件事情，也可以被视为『走到车门口、开车门、开油门、关闭车门、发动』这五件事情，从微观来说又能被视为恒河沙数件事情（对应各个微观粒子的移动）。

相比之下，即便世界上只有一个人，有足够多的信息和资源，这个人有无限的自由和想象力，可是这个人还是无法真正做到『世界上的每一件事情』。人即便不被当局或外界限制权力，能做到的还是有限。世界那么大，人只需要活在其中100个单位的地方，知道其中1000个单位的事情就够了。

所以我们宣称，随着这个人行为自由度的日益增长，对他来说，可以知道的事情不断变多，他眼中的可测集类不断变大。

小时候我对国际政治报以美好的期望，长大后尽管我还对很多事情报以积极的想象力，但某几件事情就除外了。譬如国际政治。

随着『能形成看待的事物的范围』不断增大，这样就组成了一个filtration。

这是一个哲学上非常符合实际的理解。至于什么是Xn适应了Fn呢？那就是在同一时刻下，我要做出的决策不会超出我能看待的事物的范围（言外之意就是，如果超出了，我就不做那些超出范围的决策）。这和《实变函数》课程中『E∈M』这种限制一样，是一种预防性的废话。

3. $\sigma$-algebras

$\sigma$-algebras其实是个集合系,它保证在这里头的集合,不管如何做交差并补,随便做可列次,结果都还在这个系里面.这对运算的良定义是很关键的.

https://www.zhihu.com/question/36392820
https://zhuanlan.zhihu.com/p/38119668