大部分情况下都转换为凸优化问题，并通过最优化方法来求解，因此了解相关知识就显得尤为重要了。

主要内容：

1. 问题引出
2. 凸集
3. 凸函数
4. 凸优化
5. 最优化

1、问题引出

在n维空间中，对于任意两个点，对于0<=μ<=1，则表达式μx+(1-μ)y表示x和y连线之间的所有点。

证明略。

2、凸集

定义：

对于某集合中的任意x, y两个点，若x和y连线之间的所有点（0<=μ<=1，μx+(1-μ)y）仍属于这个集合，则称此集合为凸集。

维基百科：http://en.wikipedia.org/wiki/Convex_set

直观的几何表示：

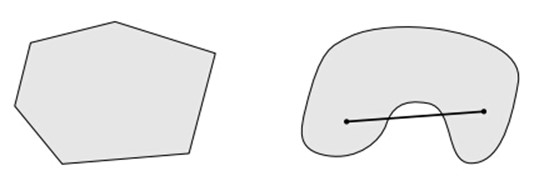
左边的是凸集，右边的不是凸集，因为右边的集合中任意两点x和y连线之间的所有点有时不属于这个集合（右图中的连线）。

3、凸函数

定义：

对于f(x)是定义在某凸集（非空的，空集也被规定为凸集）上的函数，对于凸集中的任意两点$x_1$和$x_2$，若

$f[\mu x_1+(1-\mu )x_2]<=\mu f(x_1)+(1-\mu )f(x_2)$

则称函数f(x)为凸函数。

维基百科：http://en.wikipedia.org/wiki/Convex_function

直观的几何表示：

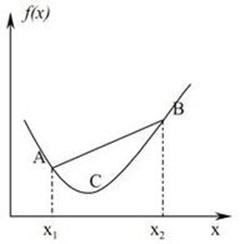
也就是说两点对应的函数值f(x1)和f(x2)的之间的连线（μf(x1)+(1-μ)f(x2)）大于等于相应的（即同一个μ值）两点之间连线（μx1+(1-μ)x2）所对应的函数值f[μx1+(1-μ)x2]。

这其实应叫下凸。

如果把上面不等式中的等号去掉，即

$f[μx_1+(1-μ)x_2]<μf(x_1)+(1-μ)f(x_2) $，其中0<μ<1

则称f(x)为严格凸函数。

凸函数的判定方法：

• 1.求导计算判断：
  

其中要求f二阶可微，表示二阶导数需大于0才是凸函数。

• 2.常用函数分析法：

指数函数是凸函数；
对数函数是凹函数，然后负对数函数就是凸函数；
对于一个凸函数进行仿射变换，可以理解为线性变换，结果还是凸函数；
二次函数是凸函数（二次项系数为正）；
高斯分布函数是凹函数；
常见的范数函数是凸函数；
多个凸函数的线性加权，如果权值是大于等于零的，那么整个加权结果函数是凸函数。

4、凸优化

定义：

同时满足如下两个条件的优化问题称为凸优化：

1）目标函数(objective function)是凸函数；

2）可行集合(feasible set)必须是凸集；

即在凸集上寻找凸函数的全局最值的过程称为凸优化。

对于一下的优化问题：

若目标函数f(x)是凸函数且可行集R是凸集，则称这样的问题为凸优化问题。

或者：

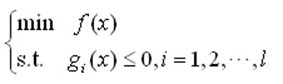
如果目标函数f(x)和共l个约束函数$g_i(x)$都是凸函数，则称这样的问题为凸优化问题。

实际上，可以证明，约束函数$g_i(x)$都是凸函数，则它的可行集是凸集。

凸优化的特点：

1）如果一个实际的问题可以被表示成凸优化问题，那么我们就可以认为其能够得到很好的解决。

2）还有的问题不是凸优化问题，但是凸优化问题同样可以在求解该问题中发挥重要的左右。比如松弛算法和拉格朗日松弛算法，将非凸的限制条件松弛为凸限制条件。

3）对于凸优化问题来说，局部最优解就是全局最优解。

4）若f(x)在非空可行集R上是严格凸函数，则全局极值点是唯一的。

也就是说如果把一个非凸优化问题转化为凸优化问题（松弛算法），则若求得一个局部最优解即为得到了全局最优解（若目标函数在可行集上是严格凸函数，则此解还是唯一的），并且凸优化问题能够比较好的得解决，因此在看压缩感知的文献时经常会看到如何如之何修改一下约束条件使之变为一个凸优化问题。

非凸优化问题如何转化为凸优化问题：

1）修改目标函数，使之转化为凸函数

2）抛弃一些约束条件，使新的可行域为凸集并且包含原可行域

实际建模中判断一个最优化问题是不是凸优化问题的方法：

1、目标函数f如果不是凸函数，则不是凸优化问题

2、决策变量x中包含离散变量（0-1变量或整数变量），则不是凸优化问题

3、约束条件写成g(x)<=0时，g如果不是凸函数，则不是凸优化问题

5、最优化

最优化问题：

最优化手段：

梯度上升（下降）法

牛顿法 / 拟牛顿法

坐标下降法：

6、参考文章

http://blog.csdn.net/jbb0523/article/details/40742955

http://m.blog.csdn.net/blog/njustzj001/47400411

https://www.cnblogs.com/AndyJee/p/5048735.html