马尔可夫链笔记

1 引言

之前学习了伯努利过程和泊松过程，它们是无记忆性，不依赖于过去的状态，今天学习了马尔可夫链，它会依赖于过去的过程，更准确的说是依赖于过去的某种状态。

2 离散时间的马尔可夫链（Markov Chain, MC）

在这里插入图片描述

另一种是转移概率图（transition probability graph），类似：
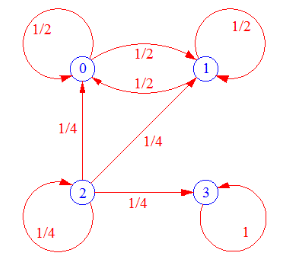
在这里插入图片描述

在这里插入图片描述

3 状态分类

一些状态被访问一次后，一定还会被继续访问，而对于另一些状态来说却不是这样的。我们来给我们的状态的可访问性提供一些严格的定义。
在这里插入图片描述
　　如果i是常返的，A(i)可以称作常返类，A(i)中的所有状态都是相互可达的，A(i)之外的状态不是从这些状态可达的。用数学语言表达就是对任意的j∈A(i)，有A(i)=A(j)。上图状态3和4可以是一个常返类，状态1自身形成一个常返类。
　　我们还可以发现一个直观的事实，从任何一个非常返状态出发，至少有一个常返状态是从它可达的，对于一个马尔可夫链至少存在一个常返状态、从而也就至少存在一个常返类．所以，我们可以得到以下结论：

一个马尔可夫链的状态集合可以分解成一个或多个常返类，加上可能的一些非常返状态。
一个常返态从它所属的类里任何一个状态出发是可达的。
从任何一个常返状态出发都不可到达非常返状态。
从一个非常返状态出发，至少有一个常返状态是可达的。

下图我们举了一些例子：
在这里插入图片描述
　　我们可以总结出这些规律：

一旦一个状态进入（或开始于）一个常返类，它将停留在这个类里，因为在这个类里的所有状态都是相互可达的，类里所有状态将被无限次的回访。
如果初始状态是非常返的，那么状态转移的路径开始部分包含非常返状态，最后一定是由来自同一个类的常返状态组成的。

所以，在一个有周期的常返类中，我们从子集的一个状态出发，一次通过每一个子集，经过d步后又重新回到原来的子集。
　　我们还有一个更简单的办法来判断一个常返类是非周期的。给定一个有周期的常返类，对于链中任意一个正时刻n，以及类中的状态i，则必存在一个或多个状态j使得rij(n)=0。原因是从状态i出发，时刻n只可能到达其中一个集合Sk。所以要证明一个给定的常返类R是非周期的，只需验证是否存在一个特定的时刻n≥1和特定的状态i∈R，使得经过n步以后，可以到达R中所有的状态，也就是说，对于所有的j∈R有rij(n)>0。反过来说也是对的，即类R如果是非周期的，当且仅当存在时刻n使得对于任何i,j∈R满足rij(n)>0。

4 稳定性质

我们之前说过，当n非常大时，rij(n)有渐进行为。如果有两个或者更多个常返状态类，很显然rij(n)的极限值一定依赖于初始状态（未来访问j的概率依赖于状态j是否和初始状态i处于相同的类），所以我们将链限定于只有一个常返类，再加上一些可能存在的非常返状态。对于单个常返类的情况研究清楚以后，多个常返类的情况也就变得简单明白了。因为我们知道，一旦状态进入一个特定的常返类，它将一直处于这个类中。所以，可以利用单一类链的渐近行为去理解具有多个常返类的马尔可夫链的渐近行为。
在这里插入图片描述

长期频率概率

考虑一个与机器相关的马尔可夫链，每天工作结束的时候机器有两种状态，正常工作或出现故障，每次出现故障时，就立即花1美元进行维修。我们应该如何建立模型，计算长期的每天平均修理费？

一种可能是将它看成未来任意一天的修理费的均值，这就需要计算故障状态的稳态概率。
另一种方法是首先可以计算n天内的总期望花费，当n很大时再除以n。

生灭过程（birth and death process）

我们来谈谈生灭过程，一个生灭过程也是马尔可夫链，它的状态是线性排列的，生灭过程的状态空间为{0,1,⋯,m}，且转移只发生在相邻状态之间，或者状态保持不变。实际生活中的排队论就是一个例子。下表示了一个生灭过程的一般结构，也介绍了转移概率的一般情况：

在这里插入图片描述

5 吸收概率（absorption probability）

前面我们考虑的是马尔可夫链的长期行为，下面我们将学习马尔可夫链的短期行为。
　　考虑开始于非常返状态的情形，我们感兴趣的是首次访问常返态的分布以及对应的到达时间的分布。在这种情况下，马尔可夫链的后续行为（到达常返态之后）是不重要的，所以我们重点讨论每一个常返态k为吸收的，即：
在这里插入图片描述

关于吸收概率方程组的解的唯一性这里就不单独证明了。
在这里插入图片描述

6 连续的马尔可夫链

我们之前讨论的都是离散时间的马尔可夫链，假设状态都是在单位时间内发生的。接下来我们要考虑连续时间的马尔可夫链，它被用于很多按照连续时间到达的过程，例如通信网络中的分布中心，其中新信号的到达是按照泊松过程到达的。
　　
　　我们将考虑一个过程，它按照一定的转移概率从一个状态转移到下一个状态，但是我们令两次转移之间的时间是一个连续随机变量，假设状态的个数是有限的，状态空间是集合S={1,⋯,m}，记Xn为第n次转移后的概率，Yn为第n次转移的时间，Tn为第n−1次转移和第n次转移的间隔时间。
　　
　　假设X0表示初始状态，令Y0=0，我们给出假设：

如果当前状态是i，到下一个转移的时间服从已给参数vi的指数分布，且独立于之前的历史过程和下一个状态。
如果当前状态是i，按照给定的概率pij到达下一个状态j，而且独立于之前的历史过程和转移到下一个状态的时间间隔。

7 Conclusion

马尔可夫链区别于一般随机过程的核心性质是转移概率pij的性质，在当前状态为i的条件下，下一个时刻为状态j的转移概率为pij，这与i所在的时刻是无关的，且独立于时刻以前的状态。所以，给定当前一个状态，未来的状态与过程的过去状态是相互独立的。
　　马尔可夫链模型通常涉及到这几个问题：

有关有限时间上过程的统计量的问题。（C-K方程）
有关马尔可夫链的稳态概率的问题。（常返的，周期的，平衡方程组，归一化方程）
有关马尔可夫链的状态转移性质的问题。（吸收概率，平均首访和回访时间）
　　最后我们也考虑连续时间的马尔可夫链在这类模型中，给定当前状态下，下一个状态由类似于离散时间的马尔可夫链的相同机制所决定。但是，直到下个转移发生的时间是指数型随机变量，参数只依赖于当前状态连续时间的马尔可夫链在许多方面可以类比离散时间的马尔可夫链，它们具有相同的马尔可夫性质（在给定当前情况下，未来与过去独立）。事实上，人们可以将连续时间的马尔可夫链看成时间轴上进行细分离散化的离散时间的马尔可夫链。建立这个联系后，连续时间的马尔可夫链与离散时间的马尔可夫链的稳态特性是相似的：假设只有一个常返类，那么处于任何状态的概率，当时间趋于无穷的时候都收敛于一个稳态概率，而且该概率不依赖于初始状态稳态概率可以通过求解平衡方程组和归一化方程得到。