我们在做机器学习、深度学习或自然语言处理等项目时，经常采用什么方法采样呢？大家马上会想到吉布斯 Gibbs 采样，今天我们来分享一种比较实用的采样方法：马尔可夫蒙特卡罗方法，吉布斯采样是其中的一种。

Markov chain Monte Carlo methods中的 Markov chain 是因为这些方法生成的序列都是马尔科夫链，每个值都只和自己前后几个值有关； Monte Carlo是因为这些方法是用随机化的方法解决确定性问题，从已知概率分布中采样出一系列符合这个分布的样本。

要弄懂MCMC的原理，我们首先得搞清楚蒙特卡罗方法和马尔科夫链的原理。个人总结如图一所示。
在这里插入图片描述
图一：马尔可夫蒙特卡罗MCMC方法

1. 蒙特卡罗方法

蒙特卡罗方法是很宽泛的一类计算方法，依赖重复的随机采样去获得数值结果。

（原文：Monte Carlo methods is a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results。）

其本质是使用随机性去解决确定性的问题。

主要用于解决三种问题：**优化，数值积分，从概率分布中采样。**原则上，蒙特卡罗方法可以用来解决任何具有概率解释的问题。根据大数定律，某一随机变量的期望可以用该变量的样本的经验均值(即样本均值)来近似。

当变量的概率分布参数化时（参数确定下来时），数学家们经常使用**马尔可夫链蒙特卡罗(MCMC)采样器。其核心思想是设计一个具有给定平稳概率分布的马尔科夫链模型。**根据遍历理论，用MCMC采样器的随机状态的经验测度来近似平稳分布。

1.1 蒙特卡罗概念及引入

蒙特卡罗方法就是生成样本，即蒙特卡罗采样。即根据某已知分布的概率密度函数 $f (x)$ ，产生服从此分布的样本 $X$ 。最早的蒙特卡罗方法都是为了解决一些求和或者积分问题。比如积分：
在这里插入图片描述
也就是说，我们最上面的均匀分布也可以作为一般概率分布函数 $p (x)$ 在均匀分布时候的特例。那么我们现在的问题转到了如何求出分布 $p (x)$ 对应的若干个样本来。

1.2 概率分布采样

上一节我们讲到蒙特卡罗方法的关键是得到 $x$ 的概率分布，那如何基于常见概率分布$$取得样本集 $x$ 呢。

在这里插入图片描述

1.3 接受-拒绝采样

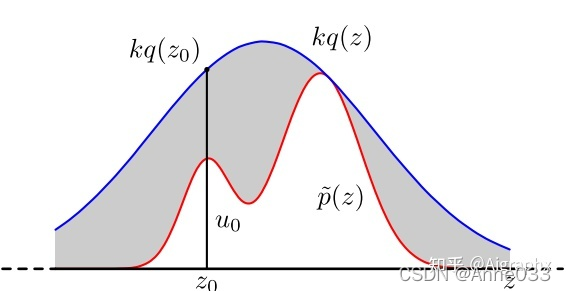
对于概率分布不是常见的分布，一个可行的办法是采用接受-拒绝采样来得到该分布的样本。 既然 $p (x)$ 太复杂在程序中没法直接采样，那么我设定一个程序可采样的分布 $q (x)$ 比如高斯分布，然后按照一定的方法拒绝某些样本，以达到接近 $p (x)$ 分布的目的，其中 $q (x)$ 叫做 proposal distribution。

在这里插入图片描述

1.4 蒙特卡罗方法缺陷

使用接受-拒绝采样，我们可以解决一些概率分布不是常见的分布的时候。但是接受-拒绝采样也只能部分满足我们的需求，在很多时候我们还是很难得到我们的概率分布的样本集。比如：

1）对于一些二维分布p(x,y)，有时候我们只能得到条件分布p(x|y) 和p(y|x) 的和,却很难得到二维分布p(x,y) 一般形式，这时我们无法用接受-拒绝采样得到其样本集。

2）对于一些高维的复杂非常见分布p(x1,x2,…,xn)，我们要找到一个合适的q(x)和 k 非常困难。

蒙特卡罗法的缺陷
通常的蒙特卡罗方法可以模拟生成满足某个分布的随机向量，但是蒙特卡罗方法的缺陷就是难以对高维分布进行模拟。对于高维分布的模拟，最受欢迎的算法当属马尔科夫链蒙特卡罗算法(MCMC)。

2.马尔科夫链方法

2.1 马尔科夫链定义

在这里插入图片描述
某一时刻状态转移的概率只依赖于它的前一个状态，我们只要能求出系统中任意两个状态之间的转换概率，这个马尔科夫链模型就能确定。每一个状态都以一定的概率转化到下一个状态，这个状态概率转化图可以用矩阵的形式表示。这就是我们常说的马尔科夫链模型状态转移矩阵。

那么马尔科夫链模型的状态转移矩阵和我们蒙特卡罗方法需要的概率分布样本集有什么关系呢？

2.2 马尔科夫链模型状态转移矩阵的性质

实验得出：从不同初始概率分布开始，代入状态转移矩阵，最终状态概率分布趋于同一个稳定的概率分布，也就是说马尔科夫链模型的状态转移矩阵收敛到的稳定概率分布与我们的初始状态概率分布无关。

这个性质对离散状态、连续状态都成立。

2.3 基于马尔科夫链采样

在这里插入图片描述

2.4 马尔科夫链采样小结

如果假定我们可以得到马尔科夫链状态转移矩阵，那么我们就可以用马尔科夫链采样得到我们需要的样本集，进而进行蒙特卡罗模拟。但是一个重要的问题是，随意给定一个平稳分布 $π\pi$ ,如何得到它所对应的马尔科夫链状态转移矩阵 $P$ 呢？这是个大问题。我们绕了一圈似乎还是没有解决任意概率分布采样样本集的问题。

幸运的是，MCMC采样通过迂回的方式解决了上面这个大问题，下面将讨论MCMC采样，以及改进版: M-H采样和Gibbs采样。

3 MCMC采样

MCMC方法包含了一类用于从特定概率分布中采样的算法。

它们是通过构建一个自身的分布接近它的平稳分布的马尔科夫链，这个马尔科夫链就是被采样的分布的一组采样值，这需要观察这个马尔科夫链一些步骤才能完成，且观察的步骤越多，得到的采样值的分布就越接近于想要的分布。

By constructing a Markov chain that has the desired distribution as its equilibrium distribution, one can obtain a sample of the desired distribution by observing[clarification needed] the chain after a number of steps. The more steps there are, the more closely the distribution of the sample matches the actual desired distribution.

MCMC方法最初是被用于计算多维积分的数值近似值。

MCMC方法从一个连续随机变量中，以和已知函数成比例的概率密度生成一组采样样本，这组样本就可以用于计算这个变量的期望和方差。

3.1 马尔科夫链的细致平稳条件

在这里插入图片描述

那么如何使这个等式满足呢？下面我们来看MCMC采样如何解决这个问题。

3.2 MCMC采样

在这里插入图片描述

好了，现在我们来总结下MCMC的采样过程。

在这里插入图片描述

3.3 M-H采样

M-H采样是Metropolis-Hastings采样的简称，这个算法首先由Metropolis提出，被Hastings改进，因此被称之为Metropolis-Hastings采样或M-H采样。M-H采样解决了我们上一节MCMC采样接受率过低的问题。

在这里插入图片描述

3.4 M-H采样总结

M-H采样完整解决了使用蒙特卡罗方法需要的任意概率分布样本集的问题，因此在实际生产环境得到了广泛的应用。

但是在大数据时代，M-H采样面临着两大难题：

在这里插入图片描述

Gibbs采样解决了上面两个问题，因此在大数据时代，MCMC采样基本是Gibbs采样的天下。

MCMC方法从一个连续随机变量中，以和已知函数成比例的概率密度生成一组采样样本，这组样本就可以用于计算这个变量的期望和方差。

3.5 吉布斯Gibbs采样基础概念

吉布斯采样就是一种MCMC方法，用于在直接采样联合分布很困难时，生成某特定多参数的概率分布的一组近似观测值。

当联合分布不被明确知道或者联合分布很难直接采样但每个变量的条件分布已知且容易采样时，吉布斯采样适用。

吉布斯采样是一种用于统计推断的方法，尤其是贝叶斯推断。它是一种随机化算法（即使用随机数的算法），是用于统计推断的确定性算法（如EM算法）的替代品。

最初的吉布斯采样是Metropolis–Hastings 算法的一个特例。但后来得到扩展，它可以被看成是一个通用的用于通过依次采样每一个变量从一组变量中采样的框架，而且可以把M-H算法，甚至更高级的算法比如 slice sampling切片采样, adaptive rejection sampling 自适应拒绝采样，合并进来实现采样过程的一些步骤。

这组生成的近似观测值可以用于近似联合概率分布；也可以去近似某个变量的边缘分布；或者近似其中部分变量的联合分布；或者计算某个变量的期望。
就像其他MCMC算法一样，吉布斯采样生成的一组近似观测值是一个马尔科夫链，即每个观测值只和附近几个值有相关性。所以如果要采样出完全独立的观测值，需要特别注意这一点。而且一般来自马尔科夫链开端的那些样本不能很好的表示原概率分布，会被去掉。而且采样值的马尔可夫链越长越有利于逼近原分布。

吉布斯采样依次从每个变量的分布中生成一个实例，基于其他变量的当前值。可以证明，这样生成的采样值序列是一个马尔科夫链，并且这个马尔科夫链的平稳分布就是我们想要采样的那个后验分布。

对于从多变量的联合分布中采样出一个向量（所有变量是向量的分量），从条件分布中采样比做积分算边缘概率简单得多。

The point of Gibbs sampling is that given a multivariate distribution it is simpler to sample from a conditional distribution than to marginalize by integrating over a joint distribution.

吉布斯采样尤其适用于采样贝叶斯网络的后验分布，因为一般贝叶斯网络就是用一组条件分布描述的。

Gibbs sampling is particularly well-adapted to sampling the posterior distribution of a Bayesian network, since Bayesian networks are typically specified as a collection of conditional distributions.