char java 回文_LeetCode刷题笔记（Java）---第1-18题

题目来自LeetCode

文章目录

全部章节

1-18题

19-40题

41-60题

61-80题

81-100题

101-120题

121-140题

1.两数之和

2.两数相加

3.无重复字符串的最长子串

4.寻找两个有序数组的中位数

5.最长回文子串

6.Z 字形变换

7.整数反转

8.字符串转换整数 (atoi)

9.回文数

10.正则表达式匹配

11.盛最多水的容器

12.整数转罗马数字

13.罗马数字转整数

14.最长公共前缀

15.三数之和

16.最接近的三数之和

17.电话号码的字母组合

18. 四数之和

全部章节

1-18题

19-40题

41-60题

61-80题

81-100题

101-120题

121-140题

1.两数之和

给定一个整数数组nums和一个目标值target，请你在该数组中找出和为目标值的那两个整数，并返回他们的数组下标。

你可以假设每种输入只会对应一个答案。但是，你不能重复利用这个数组中同样的元素。

示例:

解答：

private static int[] twoSum(int[] nums, int target) {

int[] indexs = new int[2];

Map map = new HashMap<>();

for (int i = 0; i < nums.length; i++) {

if (map.containsKey(nums[i])) {

indexs[0] = i;

indexs[1] = map.get(nums[i]);

return indexs;

}

map.put(target - nums[i], i);

}

return indexs;

}

分析：

1.需要1个长度为2的数组来保存符合条件的组合下标。

2.因为所有的数值只能使用一次，那么就需要记录下每一个数与目标数值的差，以及它的下标。可以利用HashMap来实现。差作为key，下标作为value。

过程：

只需要一层循环遍历HashMap中是否包含原给定数组中的数值，若有，则记录下该数值的下标，以及此时HashMap中该数值的所对应的value，这个value就是满足条件的另一个原给定数组中的数值所对应的下标。

若没有，则将目标值减去该数值的结果作为key，该数值的下标作为value添加到HashMap中。

2.两数相加

给出两个非空的链表用来表示两个非负的整数。其中，它们各自的位数是按照逆序的方式存储的，并且它们的每个节点只能存储一位数字。

如果，我们将这两个数相加起来，则会返回一个新的链表来表示它们的和。

您可以假设除了数字0之外，这两个数都不会以0开头。

示例：

解答：

private ListNode addTwoNumbers(ListNode l1, ListNode l2) {

ListNode root = new ListNode(0);

ListNode cursor = root;

int carry = 0;

while (l1 != null || l2 != null || carry != 0) {

int l1Val = l1 != null ? l1.val : 0;

int l2Val = l2 != null ? l2.val : 0;

int sumVal = l1Val + l2Val + carry;

carry = sumVal / 10;

ListNode sumNode = new ListNode(sumVal % 10);

cursor.next = sumNode;

cursor = sumNode;

if (l1 != null) l1 = l1.next;

if (l2 != null) l2 = l2.next;

}

return root.next;

}

分析：

1.为了保存两数相加的结果新建一个头结点root与尾指针cursor，初始指向头结点。

2.设置一个进位标示位carry，初始位0，用于记录是否进位。

3.循环条件判断：初始给定的两个链表若有一条没遍历结束，或者进位标示位不为0。

过程：

根据循环条件判断是否继续执行，判断此时链表1与链表2是否为空，若为空则此时的值为0，若不为空，则记录该值分别为l1val与l2val，将l1val、l2val、carry相加。判断是否进位，若进位carry=1，否则=0。新建一个结点，将求和值除以10的余数记录下来。使用尾插法，将该结点插入到尾指针所指向指针的后面。更新尾指针的位置。最后返回头结点之后的链表即为结果。

3.无重复字符串的最长子串

给定一个字符串，请你找出其中不含有重复字符的最长子串的长度。

示例 1:

示例 2:

示例 3:

解答：

private static int lengthOfLongestSubstring(String s) {

int maxLength = 0;

char[] chars = s.toCharArray();

int leftIndex = 0;

for (int j = 0; j < chars.length; j++) {

for (int innerIndex = leftIndex; innerIndex < j; innerIndex++) {

if (chars[innerIndex] == chars[j]) {

maxLength = Math.max(maxLength, j - leftIndex);

leftIndex = innerIndex + 1;

break;

}

return Math.max(chars.length - leftIndex, maxLength);

}

分析

1.需要一个最长记录标示，初始为0

2.将字符串转成字符数组

3.用于标记已找到最长子串，不用再判断该标记之前的部分。

过程

外层循环从0到字符串长度，用于从固定长度的字符串中找出最长的不重复的子串。

内层循环从标记位开始到此次外层循环限定的长度，判断这个范围内的最长子串。因为外层循环是逐一扩大的，所以只需要判断内层循环中的字符与外层循环限定的那个位置的字符是否相同，即可判断出字符串是否有重复。若有重复的字符出现，记录此时的长度 j(外层循环限定位置)-leftIndex(标志位)。判断此时的长度与最大记录的长度，保留最大者。修改标志位leftIndex=出现重复字符串的位置innerIndex+1。结束内层循环。

直到外层循环结束。判断 (字符串长度-标志位)与记录的最大长度的大小。返回较大者即为结果。

4.寻找两个有序数组的中位数

给定两个大小为m和n的有序数组nums1和nums2。

请你找出这两个有序数组的中位数，并且要求算法的时间复杂度为 O(log(m + n))。

你可以假设nums1和nums2不会同时为空。

示例1

示例2

解答

public double findMedianSortedArrays(int[] nums1, int[] nums2) {

int m = nums1.length;

int n = nums2.length;

int left = (m + n + 1) / 2;

int right = (m + n + 2) / 2;

return (findKth(nums1, 0, nums2, 0, left) + findKth(nums1, 0, nums2, 0, right)) / 2.0;

}

public int findKth(int[] nums1, int i, int[] nums2, int j, int k) {

if (i >= nums1.length) return nums2[j + k - 1];

if (j >= nums2.length) return nums1[i + k - 1];

if (k == 1) {

return Math.min(nums1[i], nums2[j]);

}

int midVal1 = (i + k / 2 - 1 < nums1.length) ? nums1[i + k / 2 - 1] : Integer.MAX_VALUE;

int midVal2 = (j + k / 2 - 1 < nums2.length) ? nums2[j + k / 2 - 1] : Integer.MAX_VALUE;

if (midVal1 < midVal2) {

return findKth(nums1, i + k / 2, nums2, j, k - k / 2);

} else {

return findKth(nums1, i, nums2, j + k / 2, k - k / 2);

}

分析

1.数组长度为奇数，则中位数是最中间的值；为偶数，则是最中间两个值相加/2。

2.考虑到时间复杂度的要求，使用二分查找法。

3.因为不确定奇数还是偶数，所以求两个第k个值的平均数。初始两个k分别设为(m+n+1)/2 与 (m+n+2)/2。若m+n为奇数，则两个k相同，相加求平均等于自身；若m+n为偶数，则两个k不相同，即为最中间的两个数求平均。

4.难点在于如何求第k个值，具体看下面过程。

过程

寻找第k个值的方法参数一共5个：

int[] nums1, int i, int[] nums2, int j, int k

分别表示第一个数组，第一个数组起始搜索位置，第二个数组，第二个数组起始搜索位置，要寻找的目标第k个。

首先判断第一个数组的起始位置是否超过数组长度，若超出则不需要考虑第一个数组，直接返回第二个数组中下标为 j+k-1 的数值，即为要找的第k个。减1是因为数组的下标起始是0不是1。

同理判断第二个数组的起始位置是否超过数组长度，若超过则不需要考虑第二个数组，直接返回第二个数组中下标为 i+j-1 的数值。

然后分别计算两个数组中第k/2个值的大小，记录为midval1与midval2。数组不存在第k/2数值，则设置为无限大。比较midval1midval2的大小，若midval1小，则说明数组1中前k/2个数值中没有要找的那个数字。

递归调用此方法，更新参数数组1中的起始位置为 i + k/2，k的值更新为 k-k/2。

同理若midval2小，则递归调用此方法，更新参数数组2中的起始位置为 j + k/2，k的值更新为 k-k/2

递归出口还缺一个，当k = 1时，则返回两个数组起始位置的值中较小的那一个。

5.最长回文子串

给定一个字符串s，找到s中最长的回文子串。你可以假设s的最大长度为1000。

示例1:

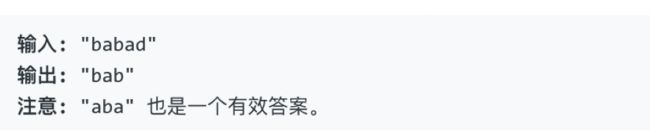
示例2:

解答

public String longestPalindrome(String s) {

if (s == null || s.length() == 0)

return "";

if (s.length() == 1)

return s;

int size = s.length();

int maxLen = 1;

int start = 0;

int[][] memo = new int[size][size];

char[] chars = s.toCharArray();

for (int i = 0; i < size; i++) {

memo[i][i] = 1;

if (i < size - 1 && chars[i] == chars[i + 1]) {

memo[i][i + 1] = 1;

start = i;

maxLen = 2;

}

for (int L = 3; L <= size; L++) {

for (int i = 0; i + L - 1 < size; i++) {

int j = L + i - 1;

if (chars[i] == chars[j] && memo[i + 1][j - 1] == 1) {

memo[i][j] = 1;

start = i;

maxLen = L;

}

return s.substring(start, start + maxLen);

}

分析

1.理解回文的意思，一个字符串正序读与反序读结果是一样的称为回文字符串。

2.采用DP的思想将复杂的问题分解成许多子问题。利用一张表来记录之前问题的结果。

3.一个长的字符串直接很难判断出最长的回文子串，可以缩小范围，限定字符串的长度，再小范围内找最长回文子串是容易的。并且回文子串(长度大于2)去掉收尾也一定是一个回文子串。

过程

首先求得给出字符串的长度size，设置maxLen标示，用于记录最长回文子串的长度，回文子串的起始位置为0，创建大小为size*size的数组，用于记录解决的子问题。

第一个for循环就是解决的最小的子问题，寻找长度为2的回文子串。memo[i][i]=1，是因为一个字符属于长度为1的回文子串。若有相邻字符一致，说明找到长度为2的回文子串，将其位置记录在二维数组中，memo[i][i + 1] = 1;记录该回文子串的起始位置与长度。

第二个两层循环用于解决长度为3到给定字符串长度范围内的最长回文子串。外层循环从L=3开始，因为长度为2的问题在前一个循环中已经解决。内层循环从字符串起始位置0开始。设 j = L + i - 1 ，表示长度为L，起始位置为i的字符串最末尾的字符的位置。判断长度为L的字符串收尾是否一致chars[i] == chars[j]，若一致并且其去掉收尾满足回文子串(memo[i + 1][j - 1] == 1)，则说明找到更长的回文子串。此时在二维数组中记录找到回文子串的位置(memo[i][j] = 1)，记录该子串的起始位置与长度。

循环结束后即可得到最长回文子串的起始位置与最大的长度。

6.Z 字形变换

将一个给定字符串根据给定的行数，以从上往下、从左到右进行Z字形排列。

比如输入字符串为"LEETCODEISHIRING"行数为3时，排列如下：

之后，你的输出需要从左往右逐行读取，产生出一个新的字符串，比如：“LCIRETOESIIGEDHN”。

请你实现这个将字符串进行指定行数变换的函数：

示例1:

示例2:

解答

public static String convert(String s, int numRows) {

char[] chars = s.toCharArray();

if (numRows == 1)

return s;

int step = numRows * 2 - 2;

StringBuffer buffer = new StringBuffer();

for (int i = 0; i < s.length(); i += step)

buffer.append(chars[i]);

for (int i = 1; i < numRows - 1; i++) {

for (int j = i; j < s.length(); ) {

buffer.append(chars[j]);

j += ((numRows - i) * 2 - 2);

if (j < s.length()) {

buffer.append(chars[j]);

j += 2 * i;

}

for (int i = numRows - 1; i < s.length(); i += step)

buffer.append(chars[i]);

return buffer.toString();

}

分析：

1.这是一道找规律的题目，按照输出顺序画图寻找规律，可以发现第一行与最后一行相同的规律，间隔numRows * 2 - 2，中间行是相同的规律。

2.使用StringBuffer效率上更快

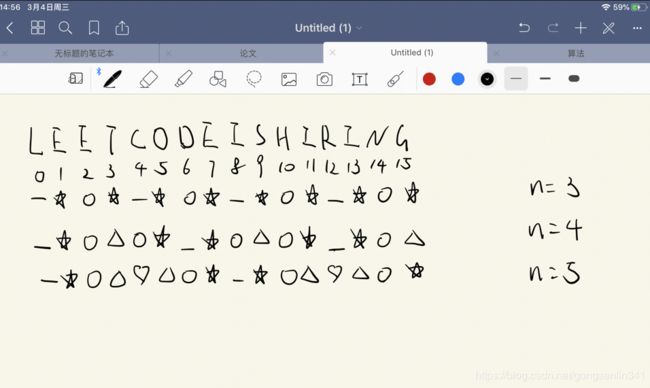
过程：

按照寻找出的规律先添加第一行再添加中间行最后是添加最后一行，即可得到结果。此题比较简单。

7.整数反转

给出一个32位的有符号整数，你需要将这个整数中每位上的数字进行反转。

示例1:

示例2:

示例3:

解答

public int reverse(int x) {

long n = 0;

while(x != 0) {

n = n*10 + x%10;

x = x/10;

}

return (int)n==n? (int)n:0;

}

分析

1.限制了整数的位数32位，所以用long来接收整数反转的结果，java中int是4个字节，long是8个字节。

2.区分好“%”与“/”的差别。

3.长字符转短字符会有数据丢失

过程

设置一个类型为long的标志n来接收答案，每次将n扩大10倍留出个位数的位置，个位数就等于给定整数x除10取余数，再将x除以10，相当于去掉最后一位的数字。循环直到x等于0。

8.字符串转换整数 (atoi)

请你来实现一个 atoi 函数，使其能将字符串转换成整数。

首先，该函数会根据需要丢弃无用的开头空格字符，直到寻找到第一个非空格的字符为止。

当我们寻找到的第一个非空字符为正或者负号时，则将该符号与之后面尽可能多的连续数字组合起来，作为该整数的正负号；假如第一个非空字符是数字，则直接将其与之后连续的数字字符组合起来，形成整数。

该字符串除了有效的整数部分之后也可能会存在多余的字符，这些字符可以被忽略，它们对于函数不应该造成影响。

注意：假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时，则你的函数不需要进行转换。

在任何情况下，若函数不能进行有效的转换时，请返回 0。

说明：

假设我们的环境只能存储 32 位大小的有符号整数，那么其数值范围为 [−231, 231 − 1]。如果数值超过这个范围，请返回 INT_MAX (231 − 1) 或 INT_MIN (−231) 。

示例1：

示例2:

示例3:

示例4:

示例5:

解答

public static int myAtoi(String str) {

long res = 0;

boolean flag = true;

int f = -1;

char[] c = str.toCharArray();

for (int i = 0; i < c.length; i++) {

if (f == -1 && (c[i] == '-' || c[i] == '+')) {

flag = c[i] == '-' ? false : true;

f = 1;

} else if (Character.isDigit(c[i])) {

res = res * 10 + (c[i] - '0');

if (res > Integer.MAX_VALUE) {

if (!flag) return Integer.MIN_VALUE;

return Integer.MAX_VALUE;

}

f = 1;

} else if (c[i] >= 32) {

if (f == -1 && c[i] == ' ') continue;

break;

}

return flag == true ? (int) res : (int) -res;

}

分析

1.此题根据给出的例子编写、修改程序即可

2.设置一个标示位，用来说明正负数

3.需要使用long类型来接收截取到的数据，防止溢出

4.java中char类型与int类型的比较是根据ASCII表进行的。参考表下面给出。

5.java中char类型与int类型的转换：

int类型转char类型，将数字加一个’0’

char类型转int类型，将数字减一个’0’

ASCII表如下：

过程

准备工作，将字符串转char数组，设置一个正负数标示位，确认是否是数字的标示位，以及用于接收答案的long类型的数据。

开始遍历转换后的char数组，判断是否有正负号存在，如果有则修改正负数标示位，并将数字标示位置1。如果没有进入下一个if判断，是否是数字，如果是则接收这一位，(利用char转int的方式再结合已得到的答案)，接收完后判断是否越界，之后将数字标示位置1。如果不是数字则进入下一个if判断，因为空格对应的ASCII码是32，其他字母也均大于32，所以判断该位字符是否大于32，如果大于32，继续判断，如果该字符是空格，并还未找到数字，则跳过此次循环进入下一轮循环，若不满足此条件则结束遍历。

最后根据正负数标示位来返回所要的答案。

9.回文数

判断一个整数是否是回文数。回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。

示例1:

示例2:

示例3:

解答

public boolean isPalindrome(int x) {

String s = "" + x;

char[] chars = s.toCharArray();

int len = chars.length;

for (int i = 0; i < len / 2; i++) {

if (chars[i] != chars[len - i - 1])

return false;

}

return true;

}

public boolean isPalindromeTwo(int x) {

int a = x;

if (x < 0) {

return false;

}

if (x < 10) {

return true;

}

if (x % 10 == 0) {

return false;

}

int t = 0;

while (x > 0) {

t = t * 10 + x % 10;

x /= 10;

}

return t == a;

}

分析：

1.相比较之前的寻找最长回文子串简单很多。

2.想法1比较收尾是否一致。

3.想法2小于0的整数不用管，0-9的整数必定是回文数，个位数为0的必定不是回文数，除此之外的数字倒转与原数字比较即可。

过程：

略

10.正则表达式匹配

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。

‘.’ 匹配任意单个字符

‘*’ 匹配零个或多个前面的那一个元素

所谓匹配，是要涵盖整个字符串 s的，而不是部分字符串。

说明:

s 可能为空，且只包含从 a-z 的小写字母。

p 可能为空，且只包含从 a-z 的小写字母，以及字符 . 和 *。

示例1:

示例2:

示例3:

示例4:

示例5:

解答

public boolean isMatch(String s, String p) {

if(s==null || p==null)return false;

char[] sc=s.toCharArray();

char[] pc=p.toCharArray();

return dp(sc,pc,0,0);

}

boolean dp(char[] s,char[] p,int i,int j){

int n=s.length;

int m=p.length;

if(j>=m) return i==n;

boolean j_match=i

if(j+1

return dp(s,p,i,j+2)||(j_match &&dp(s,p,i+1,j));

}

return j_match && dp(s,p,i+1,j+1);

}

分析

1.重点是两条匹配规则，’.‘代表任意字符，理解为a-z均可匹配；’'匹配之前的任意多个之前的一个字符。相当于复制任意份，可以是0。例如a，则可以表示“”或“aa”或“aaaaaa”任意多个a。

2.重点是如何匹配第二条规则。拆解第二条规则则就两种情况，要么匹配0个，要么匹配多个，匹配多个则可以先考虑匹配一个，利用递归来匹配接下来的。

过程

将字符串转数组，起始比较位置从每个数组下标“0”开始。首先判断第一个字符的匹配结果。接着if判断p规则数组的下一位是否是 “ * ” 号，如果是则根据 “ * ” 规则，第一种情况匹配0个，则i不变，即待匹配数组不变，j+2，则说明从符号 “ * ” 之后开始与待匹配数组匹配，递归调用dp方法继续匹配；第二种情况是匹配任意个，因为不确定匹配多少个，所以i+1，j不变，表示匹配到一位字符，递归调用dp方法匹配之后的字符。第二种情况要考虑到第一个字符匹配的结果是否一致，如果一致，则就是要看之后还有多少个相同的字符匹配。

若不满足if条件则递归调用匹配两个数字各自的下一位，结合上第一个字符匹配的结果。

还要考虑一个问题，若规则数组的起始位置已经超出了规则数组的长度，则直接返回待匹配数组的起始位置是否与其长度一致即可。

11.盛最多水的容器

给定 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 n 的值至少为 2。

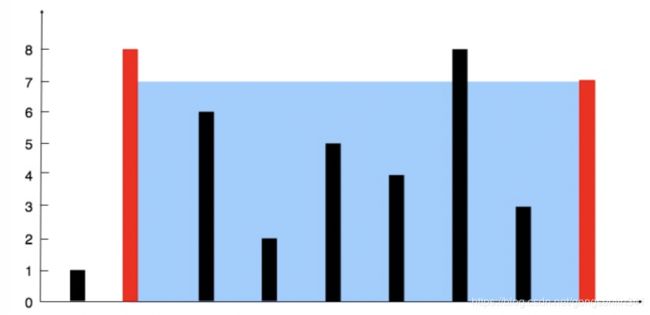
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水(表示为蓝色部分)的最大值为 49。

示例：

解答

public int maxArea(int[] height) {

int left = 0;

int right = height.length - 1;

int res = 0;

if (height.length < 2)

return -1;

while (left < right) {

res = Math.max(res, Math.min(height[left], height[right]) * (right - left));

if (height[left] < height[right])

left++;

else right--;

}

return res;

}

分析

1.此题最简单无脑的解法用暴力解决。

2.也可以使用动态规划的思想，比较已知解与变更状态后的解。而这里状态的变更就是垂线位置的改变。

3.可以先设置两个变量表示数组的开始与结尾。根据Math.min(height[left], height[right]) * (right - left)

可以求得第一个解，接下来就要考虑垂线如何移动。很显然一个容器能装多少的水取决于底部长度与较短一端有关。因为一开始已经将底部设置最大，若要改变垂线，那么底部长度是必然减小的，所以要尽量的使垂线更长，比较height[left]，height[right]，选择短的一端向另一端移动。

过程

设置变量left指向数组下标0的位置，right指向数组末尾。因为要求的n至少为2，所以要判断给的数组是否满足长度大于2。接下来就是计算最大的面积。面积等于Math.max(res, Math.min(height[left], height[right]) * (right - left))，根据上面分析的3更新left/right。直到循环结束。

12.整数转罗马数字

罗马数字包含以下七种字符： I， V， X， L，C，D 和 M。

字符数值

I 1

V 5

X 10

L 50

C 100

D 500

M 1000

例如，罗马数字 2 写做 II ，即为两个并列的 1。12 写做 XII ，即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。

通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地，数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况：

I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。

X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。

C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。

给定一个整数，将其转为罗马数字。输入确保在 1 到 3999 的范围内。

示例1:

示例2:

示例3:

示例4:

示例5:

解答

public String intToRoman(int num) {

int[] values = {1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1};

String[] m = {"M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I"};

StringBuilder builder = new StringBuilder();

for (int i = 0; i < 13; i++) {

while (num >= values[i]){

num -= values[i];

builder.append(m[i]);

}

return builder.toString();

}

分析

1.因为判断的条件很多，情况也很多种，所以可以事先将所有的判断要用到的条件以及情况都先保存在数组中。

2.StringBuilder效率更高。

过程

准备好情况与条件判断所需的数据，开始遍历，一共13种情况，在每一次的迭代中，判断更新答案即可。此题较为简单。

13.罗马数字转整数

罗马数字包含以下七种字符: I， V， X， L，C，D 和 M。

字符数值

I 1

V 5

X 10

L 50

C 100

D 500

M 1000

例如，罗马数字 2 写做 II ，即为两个并列的 1。12 写做 XII ，即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。

I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。

X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。

C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。

给定一个罗马数字，将其转换成整数。输入确保在 1 到 3999 的范围内。

示例1:

示例2:

示例3:

示例4:

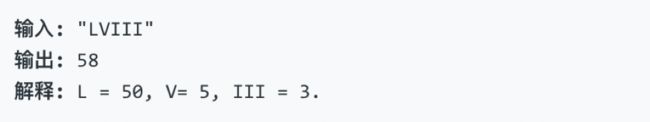
示例5:

解答

public static int romanToInt(String s) {

int[] values = {1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1};

String[] m = {"M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I"};

HashMap map = new HashMap<>();

for (int i = 0; i < 13; i++) {

map.put(m[i], values[i]);

}

char[] chars = s.toCharArray();

int res = 0;

int i = 0;

while (i < chars.length) {

if (i + 1 < chars.length)

if (map.containsKey("" + chars[i] + chars[i + 1])) {

res += map.get("" + chars[i] + chars[i + 1]);

i += 2;

continue;

}

if (map.containsKey("" + chars[i])) {

res += map.get("" + chars[i]);

i++;

}

return res;

}

分析

1.将不同的符号与数值映射，保存在hashmap中

2.遍历字符串字符，找到hashmap中存在的符号，进行结果叠加。

过程

准备工作，将13种情况的字符与数值映射关系保存在hashmap中，字符串转为字符数组。从头开始遍历字符数组，找到在hashmap中存在的key，将对应的value加到答案中。直到遍历结束。

14.最长公共前缀

编写一个函数来查找字符串数组中的最长公共前缀。

如果不存在公共前缀，返回空字符串 “”。

示例1:

示例2:

解答

public String longestCommonPrefix(String[] strs) {

if (strs == null || strs.length == 0 ) return "";

String reg = strs[0];

for (String str : strs){

while (!str.startsWith(reg)) {

if (reg.length() == 1) {

return "";

}

reg = reg.substring(0, reg.length()-1);

}

return reg;

}

分析：

1.以第一个词作为前缀的标准

2.遍历字符串数组中的字符串，比较字符串前缀是否相同，修改前缀。

过程：

首先判断字符串数组是否为空，若空则返回”“。将数组中第一个字符串作为当作最长前缀。遍历数组中的字符串，判断字符串前缀是否与已知最长前缀相同，若前缀的第一个字符都不相同，则返回””，若前缀不同则逐一缩小最长前缀。直到遍历结束，返回最长前缀。

15.三数之和

给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有满足条件且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例：

解答

public static List> threeSum(int[] nums) {

Arrays.sort(nums);

List> result = new ArrayList<>();

for (int i = 0; i < nums.length - 2; i++) {

if (i > 0 && nums[i] == nums[i - 1]) {

continue;

}

int left = i + 1, right = nums.length - 1;

if (nums[i] + nums[left] + nums[left + 1] > 0 || nums[i] + nums[right] + nums[right - 1] < 0) {

continue;

}

while (left < right) {

int sum = nums[i] + nums[left] + nums[right];

if (sum == 0) {

List triple = new ArrayList<>();

triple.add(nums[i]);

triple.add(nums[left]);

triple.add(nums[right]);

result.add(triple);

while (left < --right && nums[right] == nums[right + 1]) ;

while (++left < right && nums[left] == nums[left - 1]) ;

} else if (sum > 0) {

right--;

} else {

left++;

}

return result;

}

分析

1.先对数组进行排序，有序的数组更方便操作。

2.考虑是3个数字相加，可以先固定一个数字，变更其他两个数字。因为数组有序化，可以设置两个变量分别指向固定数字的后一位以及数组的末尾。

3.因为不能有重复的数字出现，所以第一步的有序就更凸显出它的用途。排序后的数组，相同的数字必定是相邻的，可以方便的直接掉过相同的数字。

过程

首先将数组排序，新建一个List用于接收答案。

选择固定一个数字进行遍历，因为每次是三个数字相加，所以只需要考虑前n-2个数字作为基准。

每一次的循环，先判断是否与前一位相同，若相同则跳过这一个数字。设置两个变量指向当前基准数字的后一位(left)与数组的最后一位(right)。

因为数组是有序排列的。若基准数字加它之后的两位的和大于0，则不用考虑之后的数字组合，因为之后的数字组合必定大于0;同理基准数字加最后倒数两个数字的和若小于0，则不用考虑之前的数字组合，必定小于0。

接下来确定好了基准数字后，根据基准数字与其他两个数字的和变更left与right变量。

若三者之和等于0，则将组合添加到答案中。此时根据left与后一个数字是否相同以及right与其前一位是否相同修改这两个变量。因为不能有重复数字的组合。

若三者之和大于0，则说明太大了，right指向末尾较大数字一端的变量减一。若三者之和小于0，则left变量加一。

直到left = right。此时该基准数字所有满足条件的组合已找到，进入下一次循环，基准数字更换继续寻找组合。

循环结束后，即可求得答案。

16.最接近的三数之和

给定一个包括 n 个整数的数组 nums 和一个目标值 target。找出 nums 中的三个整数，使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。

例如，给定数组 nums = [-1，2，1，-4], 和 target = 1.

与 target 最接近的三个数的和为 2. (-1 + 2 + 1 = 2).

解答

public int threeSumClosest(int[] nums, int target) {

Arrays.sort(nums);

int res = nums[0] + nums[1] + nums[2];

for (int i = 0; i < nums.length - 2; i++) {

int left = i + 1, right = nums.length - 1;

while (left < right) {

int sum = nums[i] + nums[left] + nums[right];

if (sum == target) return sum;

if (Math.abs(sum - target) < Math.abs(res - target))

res = sum;

if(sum > target)right--;

else left++;

}

return res;

}

分析

1.与上一题很相似甚至更简单了，只需要找到与目标最近的组合。

2.同样是固定一个数字，更改另外两个数字。与上题一样。

3.res接收与答案最接近的和。

过程

首先对数组进行排序，设置一个变量用来保存已经找到的最接近目标的数字组合的和。开始遍历，固定一个数字，更改另外两个数字，与上一题的过程类似。若找到的组合结果已经等于目标值则返回目标值。若组合结果距离原先已有答案的结果更接近目标，则更新答案。

如果组合的和大于目标，则高位标示位向低位移动一位，反之则低位向高位移动一位。直到循环结束。

17.电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。

示例：

解答

static Map digitsMap = new HashMap() {{

put("2", "abc");

put("3", "def");

put("4", "ghi");

put("5", "jkl");

put("6", "mno");

put("7", "pqrs");

put("8", "tuv");

put("9", "wxyz");

}};

static List res = new ArrayList();

static StringBuilder tmp = new StringBuilder();

public static List letterCombinations(String digits) {

if (digits == null) return null;

process(digits, 0);

return res;

}

private static void process(String digits, int index) {

if (index == digits.length()) {

res.add(tmp.toString());

return;

}

String letter = digitsMap.get(digits.substring(index, index + 1));

for (int i = 0; i < letter.length(); i++) {

tmp.append(letter, i, i + 1);

process(digits, index + 1);

//去掉添加的字母，开始回溯

tmp.replace(tmp.length() -1, tmp.length(),"");

}

分析

1.使用了回朔法，回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择。

2.要求的答案中的字符串长度必定和所给数字的长度是一致的，设置一个index标示位，判断满足符合长度的字符串添加的答案中。

3.每次在temp中添加来自不同字符串的一个数字。满足长度后，去掉添加的字母开始回溯。

过程

首先准备好一个HashMap，保存着数字与字符串的映射关系。需要一个List来接收答案，StringBuilder tmp，用于构造符合条件的字符串。process方法过程，判断index表示位是否等于数字的长度，若相等则将tmp加入答案中。跳出方法。若不等于，则获取index下标对应的数字，根据其映射关系得到字符串。遍历字符串，tmp添加字符，递归调用process，是为了从不同的字符串中找组合。最后是去掉添加的字母，开始回溯。

18. 四数之和

给定一个包含 n 个整数的数组 nums 和一个目标值 target，判断 nums 中是否存在四个元素 a，b，c 和 d ，使得 a + b + c + d 的值与 target 相等？找出所有满足条件且不重复的四元组。

注意：

答案中不可以包含重复的四元组。

示例：