文章目录
- 二分答案的作用
- 堆和区间
- 很糙ddp
- 线段树合并
- 网络流结论の1
- 树上莫队
- 对角线与GCD
- 区间与扫描线与方案数
- 欧拉欧拉*1
- 斯坦纳树
- 切比雪夫距离
- 二分匹配结论の1
- min-max容斥
- 计算几何の -1
二分答案的作用
- 求最大值最小ororor最小值最大
- 将求值问题转换为判断问题
- 在判断问题之间相互转换
堆和区间
当查询前kkk个最值区间时可以将开始时先将区间丢入堆中,每次取出堆顶然后将区间按照答案分裂成两个存入堆中
[NOI2010]超级钢琴【RMQ,堆】
[十二省联考2019]异或粽子【可持久化Trie,堆】
很糙ddp
将权值改为矩阵,然后将运算改成广义矩阵乘法
然后用区间数据结构维护即可
[模板]动态DP【矩阵乘法,树链剖分,线段树】
保卫王国【动态dp,最小覆盖集】
迷宫【ddp,线段树,矩阵乘法】
线段树合并
首先是必要的动态开点,然后合并时从需要合并的两颗线段树的根出发
- 若两边都有左节点那就递归左节点(右节点同理)
- 若只有一边有左节点那就让合并后的树直接连接向左节点(右节点依旧同理)
时间复杂度:O(nlogn):O(n\log n):O(nlogn)
时间复杂度证明(很糙):
我们不难发现合并的最大复杂度是最小的那颗子树的大小,那么因为只有nnn次插入那么一棵树最多nlognn\log nnlogn个节点,但是因为是最小的那颗子树大小,所以不可能每颗子树都是nlognn\ log nn logn个节点,所以对于每个节点最多被作为最小的子树合并logn\log nlogn次。
证毕
([NOI2013模拟]法法塔的奖励【权值线段树,线段树合并】)[https://blog.csdn.net/Mr_wuyongcong/article/details/95209896]
网络流结论の1
结论:最小割中对于一条边(x,y)(x,y)(x,y)在残量网络中sss可以到达xxx不能到达ttt且yyy可以到达ttt不能到达xxx那么这条边是必割边
证明:
在残量网络上sss可以到达xxx且yyy可以到达ttt那么说明若该边不割那么sss就可以通过该边到达ttt。假设在sss到xxx的路上有同样长度的一条道路且割掉后可以使sss到达xxx那么在残量网络上该边的流量必定为0,因为切割掉x−>yx−>yx−>y的流量也必定会经过该边所以在残量网络上sss就不可以到达xxx了。所以该假设不成立。
证毕
秘密任务【最短路,网络流最小割】
树上莫队
维护一个欧拉序,然后在欧拉序上进行莫队即可。
[NOI2013模拟]苹果树【树上莫队,LCA】
对角线与GCD
n∗mn*mn∗m的矩阵对角线会穿过n+m−(n,m)n+m-(n,m)n+m−(n,m)个格子
证明:
对于若(n,m)==1(n,m)==1(n,m)==1(互质)则会经过n+m−1n+m-1n+m−1个格子,所以我们可以将n∗mn*mn∗m拆分成gcd(n,m)gcd(n,m)gcd(n,m)个n/gcd(n,m)∗m/gcd(n,m)n/gcd(n,m)*m/gcd(n,m)n/gcd(n,m)∗m/gcd(n,m)的格子于是我们发现答案就是(n/gcd(n,m)+m/gcd(n,m)−1)∗gcd(n,m)(n/gcd(n,m)+m/gcd(n,m)-1)*gcd(n,m)(n/gcd(n,m)+m/gcd(n,m)−1)∗gcd(n,m)
也就是n+m−gcd(n,m)n+m-gcd(n,m)n+m−gcd(n,m)
证毕
蛋糕切割【数论,GCD】
区间与扫描线与方案数
对于x,yx,yx,y,给出若干个限制如下:
若x∈[Lxi,Rxi]x\in [Lx_i,Rx_i]x∈[Lxi,Rxi]时要求y∉[Lyi,Ryi]y\notin [Ly_i,Ry_i]y∈/[Lyi,Ryi]
那么我们可以建立一个(Lxi,Lyi,Rxi,Ryi)(Lx_i,Ly_i,Rx_i,Ry_i)(Lxi,Lyi,Rxi,Ryi)的矩阵然后扫描线求矩阵的总覆盖面积即可。
[Noip提高组模拟1]树【线段树,扫描线,倍增】
欧拉欧拉*1
φ(m!)=m!∏i=1kpi−1pi\varphi(m!)=m!\prod_{i=1}^k \frac{p_i-1}{p_i}φ(m!)=m!i=1∏kpipi−1
[SDOI2008]沙拉公主的困惑【线性筛,欧拉函数,逆元】
斯坦纳树
一张图,求一个最小权的生成树要求包含指定的点。
用状态压缩dpdpdp后用SPFASPFASPFA转移(因为有后效性)
挖宝藏(treasure)【斯坦纳树,SPFA,状压】
切比雪夫距离
定义:
disi,j=max{∣xi−xj∣,∣yi−yj∣}dis_{i,j}=max\{|x_i-x_j|,|y_i-y_j|\}disi,j=max{∣xi−xj∣,∣yi−yj∣}
用法:
- 将曼哈顿距离转换为切比雪夫距离,让(x,y)(x,y)(x,y)变为(x+y,x−y)(x+y,x-y)(x+y,x−y)。与一个点距离≤D\leq D≤D的点就变为了在改点为中心的2∗D2*D2∗D长的正方形内。
- 将切比雪夫距离转换为曼哈顿距离,让(x,y)(x,y)(x,y)变为(x+y2,x−y2)(\frac{x+y}{2},\frac{x-y}{2})(2x+y,2x−y)。然后就可以使用二维前缀和进行计算。
世界第一的猛汉王【切比雪夫距离,扫描线】
二分匹配结论の1
每个极大匹配都是完全匹配的充要条件是在完全匹配中每个联通块两边点数相同且都是满二分图。
证明
证毕
min-max容斥
max{S}=∑T∈Smin{T}∗(−1)∣T∣−1max\{S\}=\sum_{T\in S} min\{T\}*(-1)^{|T|-1}max{S}=T∈S∑min{T}∗(−1)∣T∣−1
计算几何の -1
对于一个这样的三角形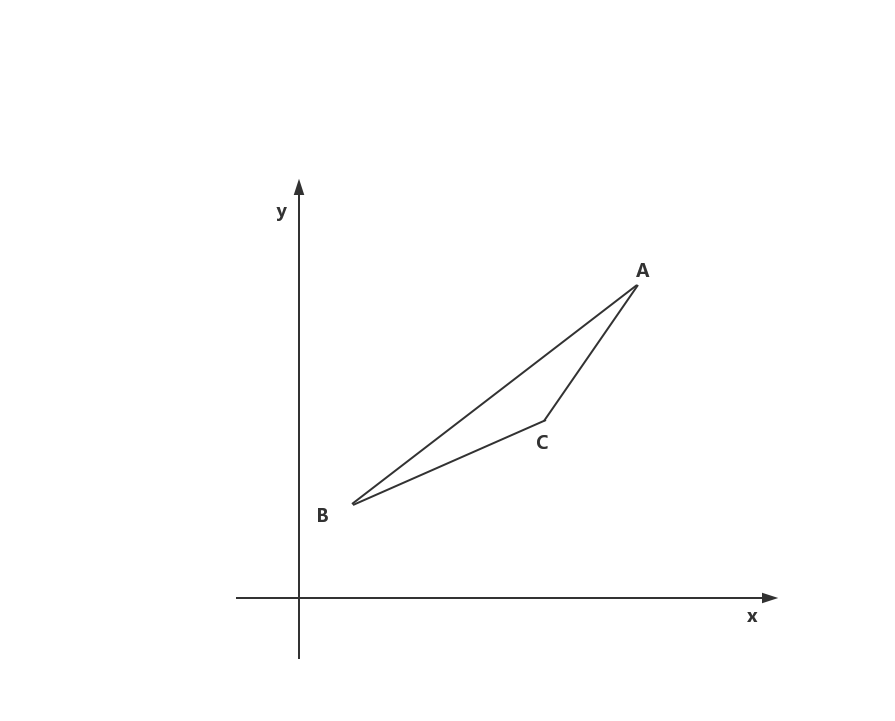
BCBCBC和CACACA中有一条斜率比ABABAB小,一条比ABABAB大

之服务实例过滤器ServerListFilter)


之类定义)


之简介)


之DataSet操作)


之视图与执行SQL)



之DataSet与RDD转换)
![P3389-[模板]高斯消元法](http://pic.xiahunao.cn/P3389-[模板]高斯消元法)

之数据加载与存储)