1、前言
上个星期完成了surging 的0.9.0.1 更新工作，此版本通过nuget下载引擎组件，下载后，无需通过代码build集成，引擎会通过Sidecar模式自动扫描装配异构组件来构建服务引擎，而这篇将介绍浅谈surging服务引擎中的rabbitmq组件和容器化部署
surging源码下载
2、Sidecar模式
比如现在比较火的Service Mesh， 谈到Service Mesh，就不得不了解下Sidecar模式，Sidecar设计模式被越来越多的关注和采用，此模式之所以称作Sidecar，是因为它类似于三轮摩托车上的挎斗。 在此模式中，挎斗附加到应用程序中，为应用程序提供支持性功能。挎斗与应用程序具有相同的生命周期：与应用程序一起创建，一起停用。 挎斗模式有时也称为搭档模式，这是一种分解模式。而surging 采用了Sidecar模式用来附加组件，而使用Sidecar模式有以下功能
共享存储空间
引擎组件部署到共享的文件目录里，服务引擎从共享的文件目录扫描引擎组件文件。
共享组件和业务的配置文件
针对于组件的配置文件部署到共享的文件目录里，服务引擎从共享的文件目录加载文件。
独立的业务服务
针对于业务可以把依赖的组件打包部署到共享的文件目录里，服务引擎从共享的文件目录扫描加载，从而部署成独立的业务服务
内置多种协议
针对于独立部署的业务服务，内置了多种协议，提供给服务和外部程序进行调用
模式特点
隔离：让组件都能够关注核心问题。比如eventbus、Logger、 netty 在实现功能的同时无需关注其它组件的实现而发生的冲突；
单一责任原则：每个组件都应该职责分开，而根据这一原则，职责应该是对应一个类、模块或者接口，从而能够独立进行处理。
内聚性/可重用性：针对组件的特性，方法可以进行重用，从而满足组件可持续扩展。
3、基于Event Bus 的Rabbitmq组件
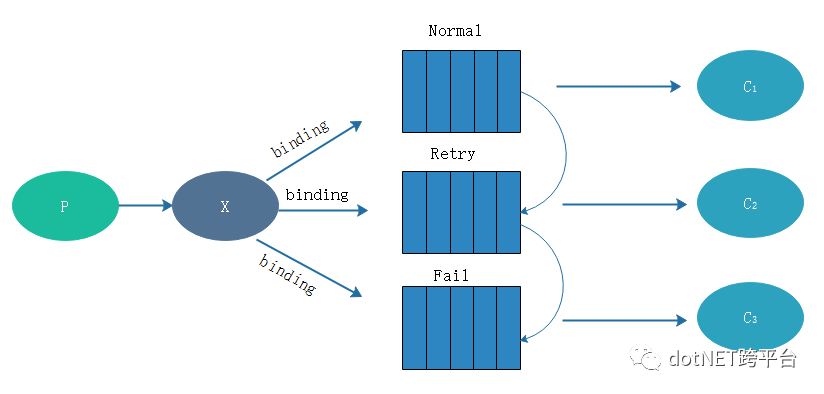
surging服务引擎扩展了基于eventbus 的rabbitmq ，组件可以选择绑定 Normal，Retry(Dead letter)，Fail ，如下图所示。
而针对于该组件有哪些应用场景呢？
商品秒杀和抢购
抢购/秒杀是如今很常见的一个应用场景，在高并发的流量访问下可以将用户放入到抢购队列中，购买成功则销毁消息。
最终数据的一致性
在大型业务中，系统一般由多个独立的服务组成，在分布式调用时候把消息放入到rabbitmq 队列中，再通过消息的幂等性来解决数据的最终一致性
订单失效处理
在购买商品/服务生成订单业务中，会设定支付时间，如果一直未支付，会直接关闭订单，而这个场景可以通过死信队列的来解决
示例代码
可以通过继承BaseIntegrationEventHandler或者IIntegrationEventHandler，再通过QueueConsumer特性进行标识，具体代码如下
可以通过以下选项去更改配置
生成绑定的队列如下图
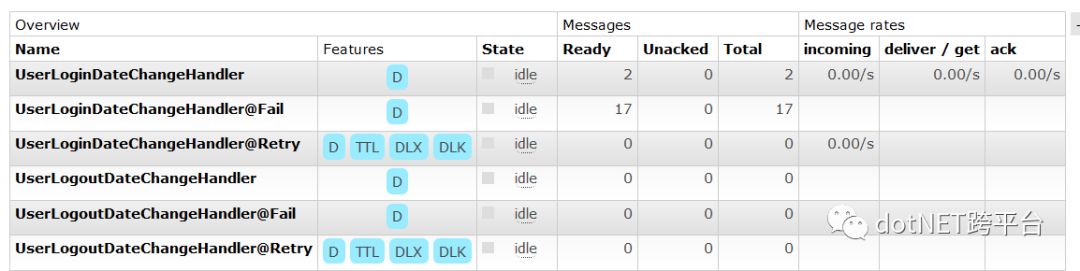
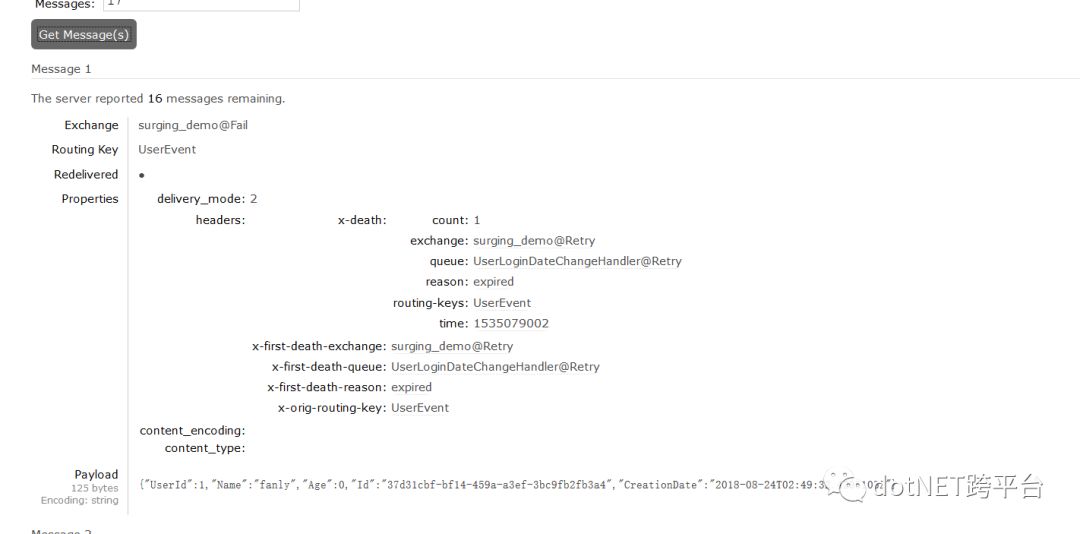
通过rabbitmq管理工具，可以通过properties来查看重试次数count 等一些信息，如下图所示
4、如何部署
surging 服务引擎构建镜像部署在docker中，可以按照业务需求自定义化引擎，也可以从 docker hub中pull镜像，可以按照如下流程从docker hub 拉取部署镜像
如何pull镜像
可以通过命令：
docker pull serviceengine/surging
可以指定具体的tag来拉取，比如需要拉取v0.9.0.2，执行以下命令
docker pull serviceengine/surging:v0.9.0.2
如何配置
1.镜像可以用环境变量设置相关参数，而通过以下的默认配置文件知晓如何通过环境变量配置参数，配置的规则：${环境变量名}|默认值
2.可以通过设置环境变量surgingpath和cachepath来指定自定义文件配置，比如，挂载/home/fanly 目录，通过以下命令参数 -v /home/fanly:/home/fanly 来设定，再通过设置以下命令参数用来设定自定义文件配置
--env surgingpath=/home/fanly/configs/surgingSettings.json--env cachepath=/home/fanly/configs/cacheSettings.json 如何启动内置引擎组件
引擎可以加载多个同一类型的引擎组件，可以通过以下配置启用哪一种引擎组件,如果是自定义的服务引擎，不需要配置以下配置，只需要按照需求引用组件
如何启动引擎
比如 pull 的镜像是serviceengine/surging:v0.9.0.2 ，可以按照以下命令进行启动
docker run --name surging --env surgingpath=/home/fanly/configs/surgingSettings.json --env cachepath=/home/fanly/configs/cacheSettings.json -v /home/fanly:/home/fanly serviceengine/surging:v0.9.0.2
7.总结
如有问题请到这里提问 ，可以加入surging互相交流QQ群：542283494，引擎组件扩展沟通群：615562965
原文地址: https://www.cnblogs.com/fanliang11/p/9543267.html
.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com
