泰勒及洛朗展开学习笔记

2020-1024=996
最近太忙了，今天好像没有写题，不过研究了一下数学hh。

2020.10.24今天又有工数课，我又没听，我记得上节工数课我看了换根dp，~~哦？好吧我没听过工数，那没事了~~，不过这次不敢那么水了，看了看书本，分析了一下书上定理的证明，突然感觉还有点意思，不过老师讲的时候好像没那么深入，由此写下自己的想法，如有错误希望指正谢谢。

一.泰勒展开证明

首先说明以下证明并不严谨，只是方便自己理解书中的证明过程，如果想要了解研究证明可以考虑看懂下面证明后转向更专业的书籍。

设函数 $f{(z)}$ 在区域 $D$ 内解析， $z0∈Dz_0 \in D$ ，圆盘 $K:|z-z_0|<R$ 含于 $D$ ，那么在 $K$ 内， $f (z)$ 能展开成幂级数
$f(z)=f(z0)+f(1)(z0)1!+f(2)(z0)2!+⋯+fn(z0)n!+…f(z)=f(z_0)+\frac{f^{(1)}(z_0)}{1!}+\frac{f^{(2)}(z_0)}{2!}+\dots +\frac{f^{n}(z_0)}{n!}+\dots$ 其中系数 $cn=12πi∫cf(ξ)(ξ−z0)n+1dξ=fn(z0)n!c_n=\frac1{2\pi i}\int_c\frac{f(\xi)}{(\xi -z_0)^{n+1}}d\xi=\frac{f^{n}(z_0)}{n!}$

按照我自己的理解，泰勒展开就是把一个函数用无穷多个非负次幂的多项式去逼近。不难想到我们需要找到一个收敛级数去逼近。

有柯西积分公式得：
$f(z)=12πi∫cf(ξ)ξ−zdξf(z)=\frac{1}{2\pi i}\int_c\frac{f(\xi)}{\xi-z}d\xi$
上面提到说用一个收敛级数逼近，观察上述式子发现这个东西 $1ξ−z\frac{1}{\xi-z}$ 好像能做点工作，于是我们会先联想到一个级数：
$11−a=1+a+a2+⋯+an+…(∣a∣<1)\frac{1}{1-a}=1+a+a^2+\dots +a^n+\dots(|a|<1)$
注意 $∣ a ∣ < 1$ 上述级数收敛，这里很重要因为在证明洛朗级数时会显现出不同。
我们下面尝试对 $1ξ−z\frac{1}{\xi-z}$ 做点工作，由于 $ξ\xi$ 是圆边界上的点，而 $z$ 是圆内的点，于是不难得知 $∣z−z0ξ−z0∣<1|\frac{z-z_0}{\xi -z_0}|<1$ （到圆心的距离之比），由此在 $z_0$ 展开 $1ξ−z\frac{1}{\xi-z}$ 时尝试先进行以下步骤
$1ξ−z=1ξ−z0−(z−z0)=1ξ−z0⋅11−z−z0ξ−z0\frac{1}{\xi-z}=\frac{1}{\xi-z_0-(z-z_0)}=\frac{1}{\xi-z_0}·\frac{1}{1-\frac{z-z_0}{\xi-z_0}}$
注意这里我们凑到 $z−z0ξ−z0\frac{z-z_0}{\xi-z_0}$ 因为 $∣z−z0ξ−z0∣<1|\frac{z-z_0}{\xi -z_0}|<1$ ，满足上述级数收敛条件。一会可以对比洛朗级数
进一步展开得：
$1ξ−z=∑n=0+∞(z−z0)n(ξ−z0)n+1\frac{1}{\xi-z}=\sum_{n=0}^{+\infty}\frac{(z-z_0)^n}{(\xi-z_0)^{n+1}}$
将上述得到的展开式子带入柯西积分公式：
$f(z)=12πi∫cf(ξ)ξ−zdξ=12πi∫cf(ξ)⋅∑n=0+∞(z−z0)n(ξ−z0)n+1dξf(z)=\frac{1}{2\pi i}\int_c\frac{f(\xi)}{\xi-z}d\xi =\frac{1}{2\pi i}\int_c {f(\xi)}·\sum_{n=0}^{+\infty}\frac{(z-z_0)^n}{(\xi-z_0)^{n+1}}d\xi$
注意积分变量是 $ξ\xi$ 与 $z$ 无关，并且积分和求和可以换序，由此得
$f(z)=12πi∫cf(ξ)⋅∑n=0+∞(z−z0)n(ξ−z0)n+1dξ=∑n=0+∞12πi∫cf(ξ)(ξ−z0)n+1dξ⋅(z−z0)nf(z)=\frac{1}{2\pi i}\int_c {f(\xi)}·\sum_{n=0}^{+\infty}\frac{(z-z_0)^n}{(\xi-z_0)^{n+1}}d\xi=\sum_{n=0}^{+\infty}\frac{1}{2\pi i}\int_c \frac{{f(\xi)}}{(\xi-z_0)^{n+1}}d\xi·(z-z_0)^n$
再由柯西高阶导数公式 $f(n)(z)=n!2πi∫cf(ξ)(ξ−z)n+1dξf^{(n)}(z)=\frac{n!}{2\pi i}\int_c\frac{f(\xi)}{(\xi-z)^{n+1}}d\xi$ 可得：

$f(z)=∑n=0+∞fz0(n)n!(z−z0)nf(z)=\sum_{n=0}^{+\infty}\frac{f^{(n)}_{z_0}}{n!}(z-z_0)^n$
证毕！

二.洛朗级数展开证明

为什么又来个洛朗级数？
自己的理解：首先我们知道泰勒级数展开条件是在一个区域内解析，区域内不能有奇点，那如果有怎么办？难道就因为这一个破奇点让我们不能深入理解这个函数？数学家们还是有办法的，首先想到的是把这个点挖掉，对没错！挖掉这个点后整个区域可以用圆环去定义，因此出现了洛朗级数以及收敛圆环的概念，这里不在赘述。

若函数 $f (z)$ 在圆环 $H:r<∣z−z0∣<R(0≤r<R≤+∞)H:r<|z-z_0|<R(0\leq r<R\leq+\infty)$ 内解析，则 $f (z)$ 在 $H$ 内可以展开成洛朗级数为
$∑−∞+∞cn(z−z0)n\sum_{-\infty}^{+\infty}c_n(z-z_0)^n$ 其中 $cn=12πi∫cf(ξ)(ξ−z0)n+1dξ,(n=0,±1,±2,…,)c_n=\frac{1}{2\pi i}\int_c\frac{f(\xi)}{(\xi-z_0)^{n+1}}d\xi,(n=0,\pm1,\pm2,\dots,)$

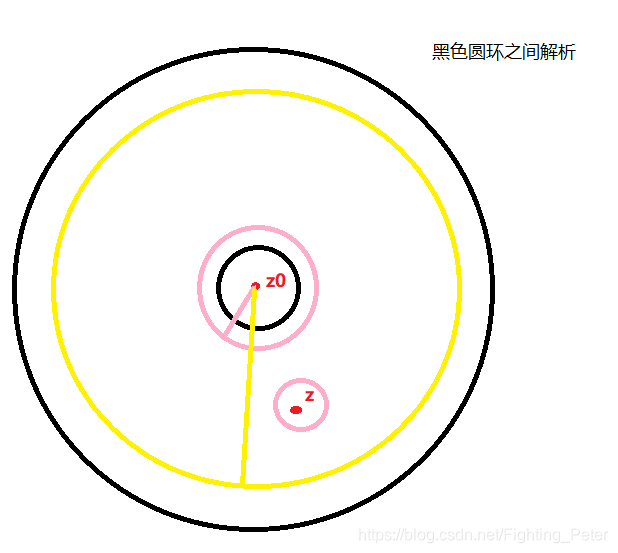
在这里插入图片描述

先定义两个圆 $Γ1:∣ξ−z0∣=ρ1,Γ2:∣ξ−z0∣=ρ2\Gamma_1:|\xi-z_0|=\rho_1,\Gamma_2:|\xi-z_0|=\rho_2$
即上图的粉色圆环和黄色圆环， $f (z)$ 在黑色圆环和黑色圆环之间解析。
对于图中圈主 $z$ 的粉色圆环定义成 $Γ\Gamma$
由复合闭路定理：
$∫Γ2f(ξ)ξ−zdξ=∫Γ1f(ξ)ξ−zdξ+∫Γf(ξ)ξ−zdξ\int_{\Gamma_2}\frac{f(\xi)}{\xi -z}d\xi=\int_{\Gamma_1}\frac{f(\xi)}{\xi -z}d\xi+\int_{\Gamma}\frac{f(\xi)}{\xi -z}d\xi$
由此可得：
$12πi∫Γf(ξ)ξ−zdξ=12πi∫Γ2f(ξ)ξ−zdξ−12πi∫Γ1f(ξ)ξ−zdξ\frac{1}{2\pi i}\int_{\Gamma}\frac{f(\xi)}{\xi -z}d\xi=\frac{1}{2\pi i}\int_{\Gamma_2}\frac{f(\xi)}{\xi -z}d\xi-\frac{1}{2\pi i}\int_{\Gamma_1}\frac{f(\xi)}{\xi -z}d\xi$
再由柯西积分公式 $f(z)=12πi∫Γf(ξ)ξ−zdξf(z)=\frac{1}{2\pi i}\int_{\Gamma}\frac{f(\xi)}{\xi -z}d\xi$ 得：
$f(z)=12πi∫Γ2f(ξ)ξ−zdξ−12πi∫Γ1f(ξ)ξ−zdξf(z)=\frac{1}{2\pi i}\int_{\Gamma_2}\frac{f(\xi)}{\xi -z}d\xi-\frac{1}{2\pi i}\int_{\Gamma_1}\frac{f(\xi)}{\xi -z}d\xi$
对于第一项来说由于 $z$ 在圆 $Γ2\Gamma_2$ 内，由此不难得出 $∣z−z0ξ−z0∣<1|\frac{z-z_0}{\xi -z_0}|<1$ ，发现这和上述证明泰勒展开时的情况相同，可以消防证明泰勒展开的方法或者直接由泰勒展开的结论得：
$12πi∫Γ2f(ξ)ξ−zdξ=∑n=0+∞cn(z−z0)n\frac{1}{2\pi i}\int_{\Gamma_2}\frac{f(\xi)}{\xi -z}d\xi=\sum_{n=0}^{+\infty}c_n(z-z_0)^n$
下面我们着重考虑如何展开后面一项 $−12πi∫Γ1f(ξ)ξ−zdξ=12πi∫Γ1f(ξ)z−ξdξ-\frac{1}{2\pi i}\int_{\Gamma_1}\frac{f(\xi)}{\xi -z}d\xi=\frac{1}{2\pi i}\int_{\Gamma_1}\frac{f(\xi)}{z-\xi}d\xi$
效仿证明泰勒展开不难得知我们需要对 $1z−ξ\frac{1}{z-\xi}$ 做点工作
注意这里点 $z$ 在圆 $Γ1\Gamma_1$ 外，于是我们有 $∣ξ−z0z−z0∣<1|\frac{\xi -z_0}{z-z_0}|<1$
，于是尝试进行下面步骤(强烈建议读者回看证明泰勒级数时的这一步，注意不同点)
$1z−ξ=1z−z0−(ξ−z0)=1z−z0⋅11−ξ−z0z−z0\frac{1}{z-\xi}=\frac{1}{z-z_0-(\xi -z_0)}=\frac{1}{z-z_0}·\frac{1}{1-\frac{\xi -z_0}{z-z_0}}$

于是得：
$1z−ξ=∑n=0+∞(ξ−z0)n(z−z0)n+1=∑n=1+∞(ξ−z0)n−1(z−z0)n=∑n=1+∞(z−z0)−n(ξ−z0)−n+1\frac{1}{z-\xi}=\sum_{n=0}^{+\infty}\frac{(\xi -z_0)^n}{(z-z_0)^{n+1}}=\sum_{n=1}^{+\infty}\frac{(\xi -z_0)^{n-1}}{(z-z_0)^{n}}=\sum_{n=1}^{+\infty}\frac{(z-z_0)^{-n}}{(\xi -z_0)^{-n+1}}$
然后积分变量是 $ξ\xi$ 与 $z$ 无关以及积分求和换序，可得：
$−12πi∫Γ1f(ξ)ξ−zdξ=∑n=1+∞12πi∫Γ1f(ξ)(ξ−z0)−n+1dξ⋅(z−z0)−n-\frac{1}{2\pi i}\int_{\Gamma_1}\frac{f(\xi)}{\xi -z}d\xi=\sum_{n=1}^{+\infty}\frac{1}{2\pi i}\int_{\Gamma_1}\frac{f(\xi)}{(\xi -z_0)^{-n+1}} d\xi·(z-z_0)^{-n}$
我们让 $c−n=12πi∫Γ1f(ξ)(ξ−z0)−n+1dξ,(n=1,2,3,…,)c_{-n}=\frac{1}{2\pi i}\int_{\Gamma_1}\frac{f(\xi)}{(\xi -z_0)^{-n+1}} d\xi,(n=1,2,3,\dots,)$
即可得到：
$f(z)=∑n=0+∞cn(z−z0)n+∑n=1+∞c−n(z−z0)−n=∑n=−∞+∞cn(z−z0)nf(z)=\sum_{n=0}^{+\infty}c_n(z-z_0)^n+\sum_{n=1}^{+\infty}c_{-n}(z-z_0)^{-n}=\sum_{n=-\infty}^{+\infty}c_n(z-z_0)^n$
证毕！！！