1. 前言

最近在看《架构整洁之道》一书，书中反复提到了面向对象编程的 SOLID 原则（在作者的前一本书《代码整洁之道》也是被大力阐释），而面向切面编程（Aop）作为面向对象编程的有力补充，对实践整洁代码更是如虎添翼。

除了整洁之道系列的影响外，本文还致敬、借鉴、补充了Aspect Oriented Programming (AOP) in C# with SOLID一文。

1. Aop 是什么？

在讨论 Aop 之前，我们可以先看看一段很常见的代码。

这是一段很典型的面向过程的代码，我们可以看到有相同的异常处理逻辑，如果我们想要避免重复的代码，我们至少可以把异常处理封装一下:

代码简洁了很多，但是我们实际上是将真实的方法代码与日志代码纠缠在一起，违反了 单一责任原则 。有没有一种可能，让我们不需要在原来的代码上显式调用 TryCache 呢？

一个可能的答案是借助 AOP 来解决。使用 AOP，我们可以在不改变原来代码的前提下，添加额外的单元功能（如异常处理，日志处理、重试机制等）。 AOP 可以把原来一大串的面向过程的代码重构成多个部分，聚焦于每一小部分，使我们的代码 可读性 和 维护性 更高，避免了 代码重复和代码纠缠 的问题。

2. 装饰器实现 AOP

C# 可以使用的 Aop 框架有很多，在我们谈论他们之前，我们可以先利用语言自带的特性，实现基础的 AOP 效果。 最简单的形式莫过于 装饰器模式 ，它的雏形大致如下：

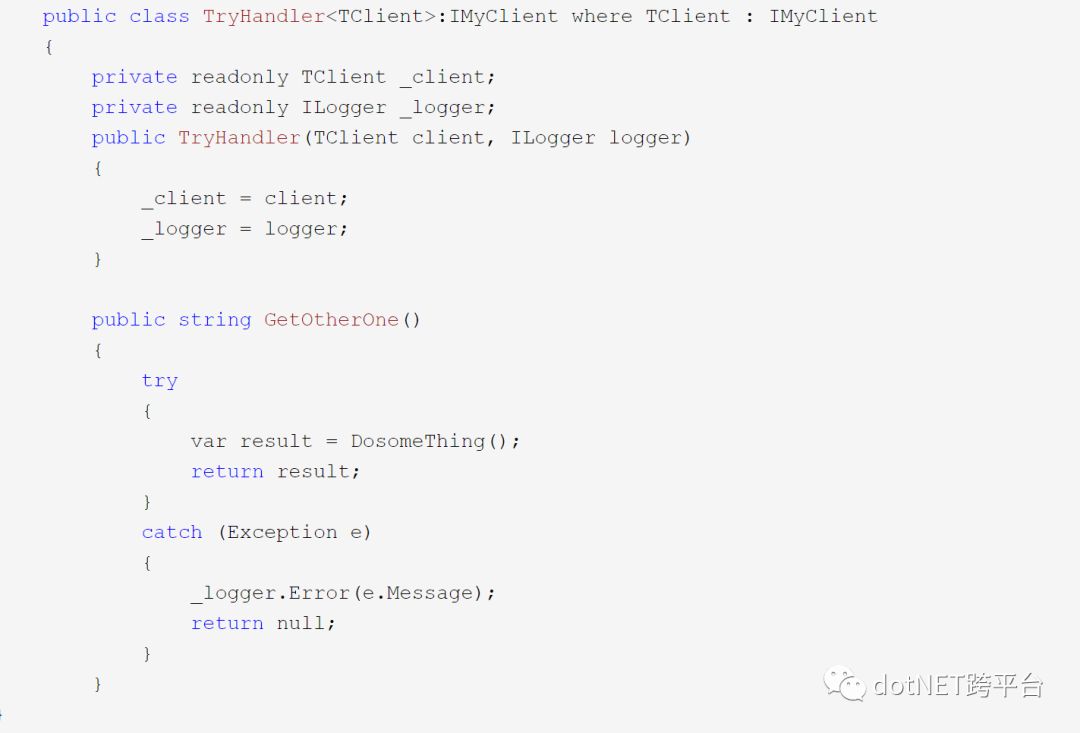
可以看到装饰器只是在原来的对象上面扩展，符合 开放封闭原则。我们在调用的时候，只需显式创建装饰实例对象。

 var tryClient=new TryHandler<MyClient>(new MyClient());tryClient.GetOtherOne();

细心的读者可能还会发现，我们还可以在这个日志装饰器上面再附加一个装饰器，比如一个针对结果处理的装饰器。

var resultClient=new ResultHandler<TryHandler<MyClient>>(tryClient);

但是这样的调用方法还是不尽人意，想象如果某个对象有三四个装饰器，那么我们创建实例的时候就需要多次传递。一个解决方法是 借助依赖注入 (DI) ，只需注册一次服务类型，避免通过创建实例来获取对象。另外，对于 .net core自带的 DI 来说，更便捷的方法是借助开源类库Scrutor 来注册装饰器对象。

services.Decorate<IMyClient, TryHandler<MyClient>>();
services.Decorate<IMyClient, ResultHandler<MyClient>>();

虽然解决了易用性，但是我们很快就发现了另一些不尽人意的地方，装饰器模式只能适用于 特定的类型，约束是比较强的。如果我们希望我们示例中的装饰器可以实现通用，就需要找别的方法了。

3. 动态代理实现 Aop

动态代理是指运行时生成，通过隐式重写方法来附加额外的功能，而其中最流行的莫过于 Castle DynamicProxy了。

Castle DynamicProxy 的常规用法是继承 IInterceptor 接口，通过实现 Intercept 方法来处理代理的逻辑。

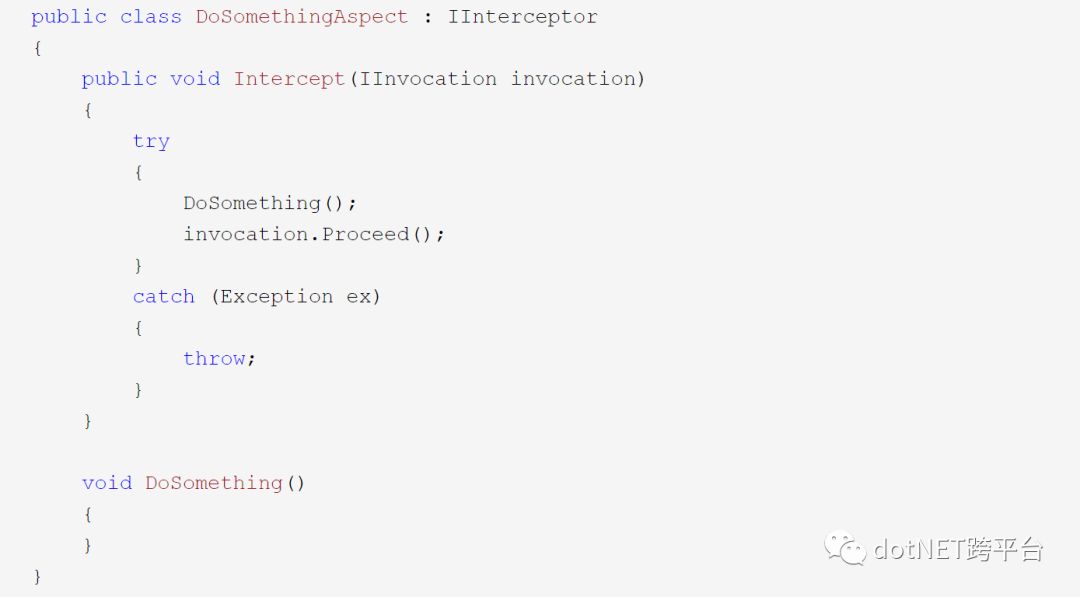
在调用的时候，类似装饰器一样需要创建代理实例。

有很多开源项目在使用 Castle DynamicProxy，其稳定性和可靠性是值得信赖的，更多的使用方法可以参照官方示例或者第三方开源项目的代码。需要特别注意的是，Castle DynamicProxy 只能作用于接口或者虚方法，这是动态代理的特性（局限）。

除了 Castle DynamicProxy 外， AspectCore也是一个不错的选择。AspectCore 的快速简单应用通过继承 AbstractInterceptorAttribute 的 Attribute类来标记并拦截代理对应的接口或者虚方法（更详细的用法可以参考 作者写的使用方法）。

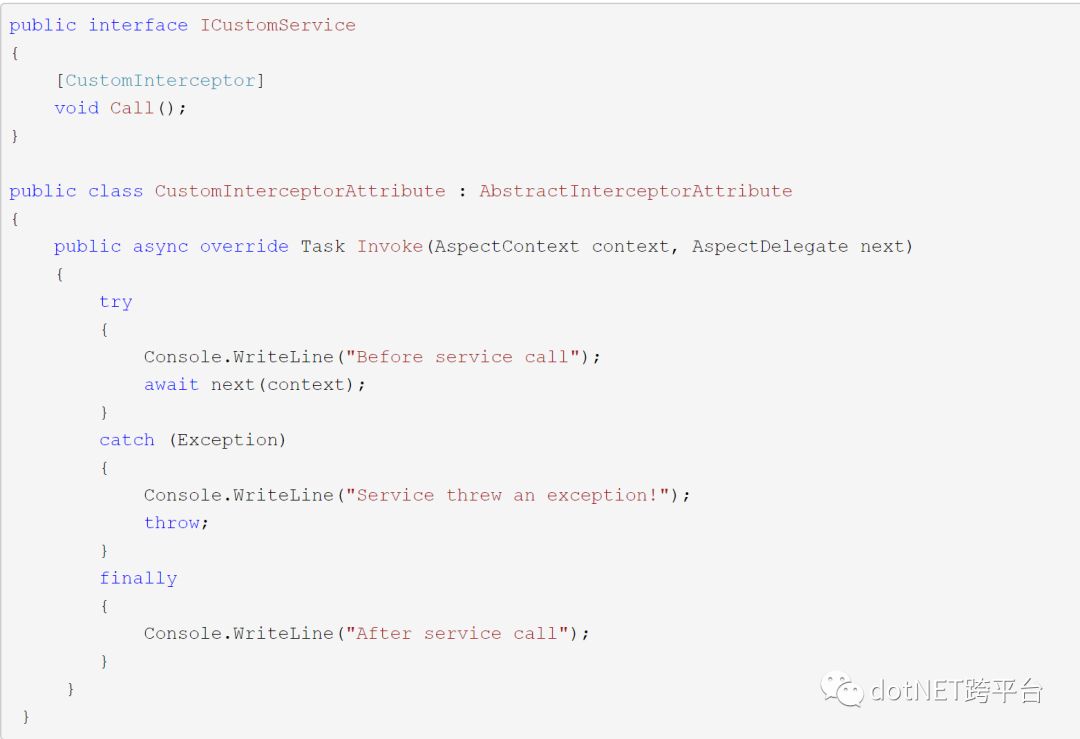
虽然易用性很好，但是要注意使用的场合，如果是在低层次（如基础设施层、应用入口层等）或者特定的应用模块内使用，对整体架构影响不大。如果是在高层次（逻辑层、核心层、领域层等）使用，则会带来不必要的依赖污染。

所以并不是推荐使用这种 Attribute 拦截代理的方式，好在 AspectCore 的设计考虑到解耦的需要，可以在单独配置代理拦截。

serviceCollection.ConfigureDynamicProxy(config =>{config.Interceptors.AddTyped<CustomInterceptorAttribute>(Predicates.ForMethod("ICustomService", "Call"));
});

但是不管是 Castle DynamicProxy 还是 AspectCore 都只能作用与接口或者虚方法，这也是动态代理的局限（特性）。如果我们想要在不受限制地在非虚方法上实现 AOP 的效果，就需要别的方法了。

4. 编译时织入实现 AOP

进行 AOP 的另一种方法是通过编译时织入，在编译的程序集内部的方法中添加额外的 IL 代码，附加我们想要的功能。

PostSharp 是其中比较流行的一种，然而由于其商业化的性质，在这里不做过多介绍。开源方面，Fody 是其中的佼佼者。

Fody 在编译时使用 Mono.Cecil 修改 . net 程序集的 IL 代码。如果你没有 IL 代码方面的知识，可以直接使用基于 Fody 开发的插件。其中最流行的插件是Costura和 Virtuosity。Costura 将依赖项作为资源嵌入，实现多个 DLL 文件合并成一个 exe 的功能,而 Virtuosity 则是在构建的时候将所有成员更改为 virtual ，重写 ORM （如EF的导航属性、NHibernate）、 Mock（RhinoMocks、NMock）以及前面提到的动态代理中需要 virtual 的地方为 virtual。

Fody 中的插件还有很多，除了 Costura 和 Virtuosity 之外，我个人还使用过 MethodDecorator，实现编译时重写类的方法或者构造函数来实现 AOP 的效果。

所有 Fody 的插件，首先都必须引入一个 FodyWeavers.xml ，并声明使用的插件。

<?xml version="1.0" encoding="utf-8"?><!--FodyWeavers.xml--><Weavers><MethodDecorator /></Weavers>

不同的插件在后面的使用方法会有所不同，以 MethodDecorator 为例，我们需要新建一个特定格式的 Attribute 类，然后标记在特定的类方法上面。

最后还需要一个 AssemblyInfo.cs 来配置哪些 Attribute 类产生作用。

//AssemblyInfo.csusing System;
[module: FodyTest]

重新编译生成，在输出中还可以看到 Fody 的输出。

既然我们可以在编译时织入 IL 代码，那么我们是不是可以提前生成我们想要的 AOP 效果，比如说借助代码生成器。

5. 代码生成器实现 AOP 效果

T4是常见的文本生成框架，我们可以使用此工具在设计时生成代码。前面我们提到过装饰器模式有特异性的问题，只能针对特定类型实现 AOP 效果，而借助代码生成器，我们可以直接生成对应的代码模板，避免了重复的劳动。由于我个人对 T4 没什么使用经验，有兴趣的读者可以参考Aspect Oriented Programming (AOP) in C# via T4一文。

除了 T4 之外，Roslyn 也是一个强有力的工具，已经有人基于 Roslyn 实现 AOP 的效果，将 Roslyn 封装为 dotnet 全局工具 ，针对特定的文件插入指定的代码段，有兴趣的读者可以参考 AOP_With_Roslyn 的代码示例。

结语

AOP 是我们 避免代码重复 和 增强代码可读性 的有力工具，是我们编写整洁代码的有力保证，借助 C# 语言自身的特性和诸多强大的开源工具，使我们更专注于代码功能。

原文地址: https://www.cnblogs.com/chenug/p/9848852.html

---

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com