syksykCCC题解
iamhpp题解
首先说明，下面图片来自第一篇博客，下面代码照抄第二篇博客
对没有啥是自己写的（因为我太菜~~

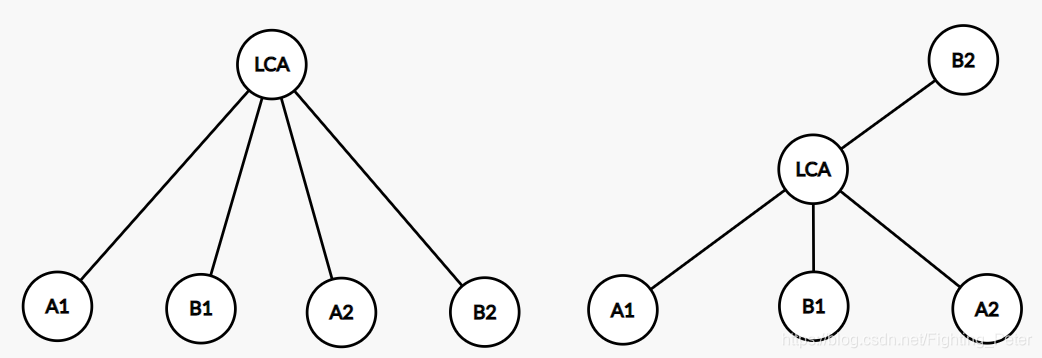
从上图可以看出两条链只有一个交点可能有两种情况

• 交点是两条链的LCA
• 交点是一条链的LCA而不是另一条

这两种情况的公共点就是：交点一定是一条链的LCA，因此我们从LCA考虑计数

对于第一种情况，如果存在一条链$x_0⇝y_0$与$x⇝y$满足条件，一定有$LCA(x_0,y_0)=LCA(x,y)$并且$x,y,x_0,y_0$分别处在$lca$的4棵子树中。
首先每次考虑相同LCA的链，因而第一个条件满足，第二个条件我们每条链记录$x$处于lca的$a$子树中，而$y$处于lca的$b$子树中，也就是如果lca是$x$的$k$级祖先，那么$a$是$x$的$k-1$级祖先（倍增跳一下即可）链的情况，把$a$设为$-1$

有了上面信息，我们考虑一条链$x⇝y$，那些和它LCA相同的链$x_0⇝y_0$对答案有贡献当且仅当$a,b,a_0,b_0$是4个不同的值，这可以用容斥原理计算

对于第二种情况，对于上图考虑$A_1⇝A_2$这条链存在多少条像$B_1⇝B_2$的链，首先不难发现$B_1⇝B_2$的LCA的深度一定严格小于$A_1⇝A_2$的LCA，也就是如果想要和$A_1⇝A_2$配对对答案产生贡献，那么其链的LCA深度一定较小，因此考虑按照LCA深度排序依次处理。

每次只需要统计LCA子树中有多少像$B_1$这样的点（在LCA的子树中并且不与$A_1,A_2$在同一子树）找个支持单点修改子树查询的数据结构即可，这里用dfs序+树状数组统计。

#define IO ios::sync_with_stdio(false);cin.tie();cout.tie(0)
#pragma GCC optimize(2)
#include<map>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
using ll=long long;
using pii=pair<int,int>;
constexpr int N=300010;
int h[N],e[2*N],ne[2*N],idx;
void add(int a,int b){e[idx]=b,ne[idx]=h[a],h[a]=idx++;}
int n,m;
int dep[N],fa[N][21],dfn[N],sz[N],timestamp;
void dfs(int u)
{dfn[u]=++timestamp;sz[u]=1;for(int i=h[u];i!=-1;i=ne[i]){int v=e[i];if(v==fa[u][0])continue;dep[v]=dep[u]+1;fa[v][0]=u;for(int k=1;k<=20;k++)fa[v][k]=fa[fa[v][k-1]][k-1];dfs(v);sz[u]+=sz[v];}
}
int lca(int u,int v)
{if(dep[u]<dep[v]) swap(u,v);for(int k=20;k>=0;k--)if(dep[fa[u][k]]>=dep[v]) u=fa[u][k];if(u==v) return u;for(int k=20;k>=0;k--)if(fa[u][k]!=fa[v][k]) u=fa[u][k],v=fa[v][k];return fa[u][0];
}
int up(int u,int d)// 从u向上跳d步
{if(d<=0) return u;for(int k=20;k>=0;k--)if(d>>k&1) u=fa[u][k];return u;
}
struct node
{int x,y,a,b,lca;
}q[N];
int fw[N];
int lowbit(int x){return x&-x;}
void update(int k,int x){for(;k<=n;k+=lowbit(k)) fw[k]+=x;}
int query(int k){int res=0;for(;k;k-=lowbit(k)) res+=fw[k];return res;}int main()
{IO;cin>>n;memset(h,-1,sizeof h);for(int i=1;i<n;i++){int u,v;cin>>u>>v;add(u,v),add(v,u);}dep[1]=1;dfs(1);cin>>m;for(int i=1;i<=m;i++){int x,y;cin>>x>>y;int anc=lca(x,y);int a=up(x,dep[x]-dep[anc]-1),b=up(y,dep[y]-dep[anc]-1);if(a==anc) a=-1;if(b==anc) b=-1;if(a>b) swap(a,b),swap(x,y);q[i]={x,y,a,b,anc};}sort(q+1,q+1+m,[](const node &i,const node&j){if(dep[i.lca]!=dep[j.lca]) return dep[i.lca]<dep[j.lca];return i.lca<j.lca;});ll ans1=0,ans2=0;for(int i=1;i<=m;i++){map<pii,int> f;map<int,int> cnt;int j=i;while(j<=m&&q[j].lca==q[i].lca) j++;//lca相同的一起统计for(int k=i;k<j;k++){int x=q[k].x,y=q[k].y,a=q[k].a,b=q[k].b,anc=q[k].lca;ans1+=k-i-cnt[a]-cnt[b]+f[{a,b}];if(a!=-1) cnt[a]++;if(b!=-1) cnt[b]++;if(a!=-1&&b!=-1) f[{a,b}]++;}i=j-1;}for(int i=1;i<=m;i++){int j=i;while(j<=m&&dep[q[j].lca]==dep[q[i].lca]) j++;//深度相同的一起统计for(int k=i;k<j;k++){int x=q[k].x,y=q[k].y,a=q[k].a,b=q[k].b,anc=q[k].lca;ans2+=query(dfn[anc]+sz[anc]-1)-query(dfn[anc]-1);if(a!=-1) ans2-=query(dfn[a]+sz[a]-1)-query(dfn[a]-1);if(b!=-1) ans2-=query(dfn[b]+sz[b]-1)-query(dfn[b]-1);}for(int k=i;k<j;k++) update(dfn[q[k].x],1),update(dfn[q[k].y],1);i=j-1;}cout<<ans1+ans2<<'\n';
}