题目描述

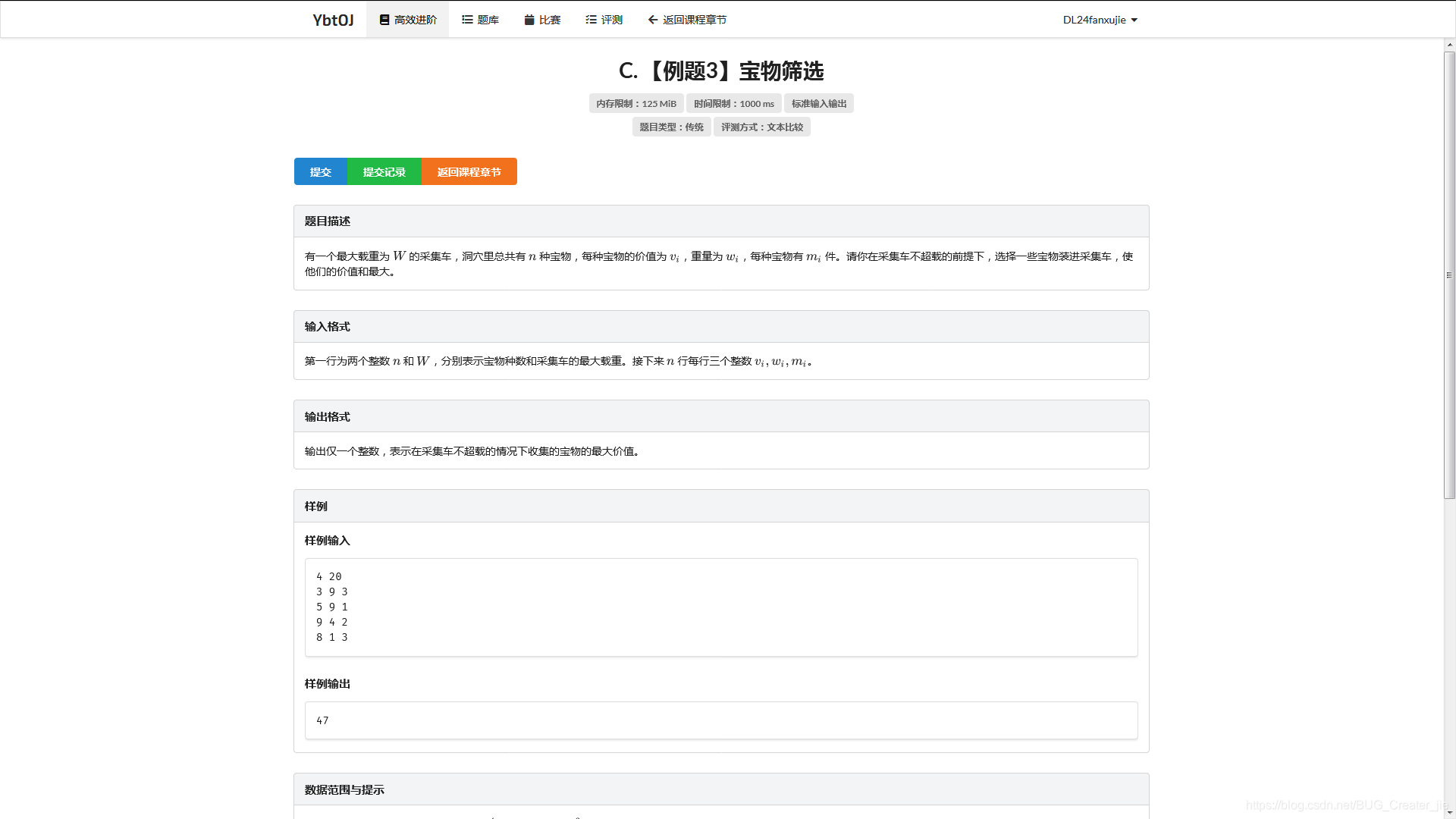
解析

朴素算法

首先考虑朴素算法
把数量为num的物体拆成num个子物体
其价值与重量是原物体的1，2，3…num倍
然后当成独立的物体求就行了
注意应该先枚举重量，再枚举子物体
因为这些子物体是不能同时取的 (因为同时取时，总个数可能会超过num）
时间复杂度：nwm
（这题这做法也能过就离谱）

代码

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iostream>
#define ll long long
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
const int N=1e6+100;
int m,n;
int W,f[N];
struct node{int v,w,num;
}p[N];
int main(){scanf("%d%d",&n,&W);for(int i=1;i<=n;i++){scanf("%d%d%d",&p[i].v,&p[i].w,&p[i].num);}for(int i=1;i<=n;i++){for(int ww=W;ww>=p[i].w;ww--){for(int k=1;k<=p[i].num;k++){if(p[i].w*k>ww) break;f[ww]=max(f[ww],f[ww-p[i].w*k]+k*p[i].v);}}}int ans=0;for(int i=0;i<=W;i++){ans=max(ans,f[i]);}printf("%d",ans);return 0;
}
/*
4 20
3 9 3
5 9 1
9 4 2
8 1 3
*/

二进制优化

刚才的枚举拆分显然十分低效
我们如何才能把物品拆分的效率提高呢？
我们尝试把每样物品拆成完全独立的物品
（也就是说可以同时取）
那么我们的拆分应不重不漏，也就是要满足以下条件：

1.加在一起不能超过总数量
2.能组合表示出1-num的所有数

显然要考虑二进制
定义sum数组：

sum[k]= 2⁰ + 2¹ +2²+… + 2^k

找到一个最大的k，满足：

sum[k]<=num

再让：

R=num-sum[k]

这样我们把物品拆成k+2个
其大小分别为：

2⁰、 2¹、2²、… 2^k、R

由于R是减出来的，加起来肯定不会超过num，条件1成立了

第二个条件，能表示出1-num的所有数的证明，可以分成两部分：
1.对于<=sum[k]的数，显然可以用2的0-k次幂用二进制拆分表示出来

2.对与>2^k的数A，把它减去R，也就是先拆出来一个R，由R的定义可得：

A-R <= num-R = sum[k]

这样减去后又是一个<=sum[k]的数，就转化为情况1了
条件二证毕
（具体的代码实现中，我预处理了一个数组q[i]存储num为i时符合条件的k值）
时间复杂度：nwlog（m）

代码

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iostream>
#define ll long long
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
const int N=1e6+100;
int m,n;
ll W,f[N];
struct node{int v,w,num;
}p[N];
int mi[50],q[N],sum[50];
void solve(){mi[0]=1;for(int i=1;i<=30;i++) mi[i]=mi[i-1]*2;sum[0]=1;q[1]=q[2]=0;int res=1,now=3;for(int k=1;k<=18;k++){res+=mi[k];for(int i=now;i<res;i++) q[i]=k-1;now=res;sum[k]=res;}
}
int main(){scanf("%d%d",&n,&W);for(int i=1;i<=n;i++){scanf("%d%d%d",&p[i].v,&p[i].w,&p[i].num);}solve();for(int i=1;i<=n;i++){int k=q[p[i].num];for(int j=0;j<=k;j++){ll nw=p[i].w*mi[j],nv=p[i].v*mi[j];for(int p=W;p>=nw;p--){f[p]=max(f[p],f[p-nw]+nv);}}int r=p[i].num-sum[k];ll nv=p[i].v*r,nw=p[i].w*r;for(int p=W;p>=nw;p--){f[p]=max(f[p],f[p-nw]+nv);}}ll ans=0;for(int i=0;i<=W;i++){ans=max(ans,f[i]);}printf("%lld",ans);return 0;
}
/*
4 20
3 9 3
5 9 1
9 4 2
8 1 3
*/

thanks for reading!