题目：

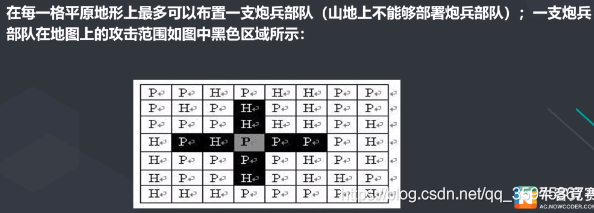
n*m个网格，有平原，有山地，平原可以放部队，部队攻击范围如图（不受地形影响）（H为山地，P为平原）

题解：

确定状态：
因为每个炮可以打到两行，所以每一行放置方式与他放置的情况有关
dp[i][j][k]表示第i行为状态j，第i-1行为状态k时所用的最大炮兵数
也就是同时记录两行状态，根据已知的两行状态推下一行
状态转移：
dp[i][j][p]=max(dp[i][j][p],dp[i-1][p][q]+num[j])
q被枚举
第i行状态：j
第i-1行状态：p
第i-2行状态：q
j，p，q不能发生冲突
任意1左右两边两位都不是1
((i&(i>>1))==0) && ((i&(i>>2)) ==0)
且1的位置必须是平原
优化：保存符合条件的二进制串，只枚举自身符合要求的二进制串

代码：

#include <cstdio>
#include <algorithm>
#include <iostream>
#include <vector>
#include <map>
#include <queue>
#include <set>
#include <ctime>
#include <cstring>
#include <cstdlib>
#include <math.h>
using namespace std;
typedef long long ll;
//#define ll long long
const ll N = 2e3 + 20;
const int maxn = 5e5 + 20;
const ll mod = 1000000007;
ll inv[maxn], vis[maxn], dis[maxn], head[maxn], dep[maxn], out[maxn];
ll fac[maxn], a[maxn], b[maxn], c[maxn], pre[maxn], cnt, sizx[maxn];
vector<ll> vec;
char s[maxn];
//typedef pair<ll, ll> p;
//priority_queue<p, vector<p>, greater<p> > m;
ll sum[maxn];
ll max(ll a, ll b) { return a > b ? a : b; }
ll min(ll a, ll b) { return a < b ? a : b; }
ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; }
ll lcm(ll a, ll b) { return a * b / gcd(a, b); }
void swap(int &x, int &y) { x ^= y, y ^= x, x ^= y; }
map<ll, ll> mp;
ll ksm(ll a, ll b)
{a %= mod;ll ans = 1ll;while (b){if (b & 1)ans = (ans * a) % mod;a = (a * a) % mod;b >>= 1ll;}return ans;
}
ll lowbit(ll x)
{return x & (-x);
}
//int dx[105], dp[105], nc[105], w[105];
int dp[105][105][105];//存i行,第j状态,和上一行的k状态的最大炮兵数量
int stk[N], np[N], sp[105];//行合法状态，合法状态的炮兵个数，山地的分布01串
int getsum(int x)//求x的二进制状态中炮兵的数量
{int ans = 0;while (x){if (x & 1)ans++;x >>= 1;}return ans;
}
int main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int t, n, m, k;// cin>>t;// while(t--)// {string s;cin >> n >> m;for (int i = 1; i <= n; i++){cin >> s;for (int j = m - 1; j >= 0; j--)if (s[j] == 'H')sp[i] += (1 << j);//累加得每一行山地的分布串}// }k = 1;for (int i = 0; i < (1 << m); i++)//枚举长度为m的可行状态{if ((!(i & (i << 1))) && (!(i & (i << 2))))stk[k] = i, np[k++] = getsum(i);}for (int i = 1; i < k; i++)//初始化dp[][][]第一行{if (!(sp[1] & stk[i]))dp[1][i][1] = np[i];}for (int i = 2; i <= n; i++){for (int j = 1; j < k; j++){if (sp[i] & stk[j])//判断当前状态和山地是否重叠continue;for (int x = 1; x < k; x++){if ((stk[x] & sp[i - 1]) || (stk[x] & stk[j]))//判断当前状态和山地和上一个状态是否有重叠continue;for (int y = 1; y < k; y++){if ((stk[y] & stk[x]) || (stk[y] & stk[j]) || (stk[y] & sp[i - 2]))continue;//判断当前状态和山地和上一个状态，和上上一个状态是否有重叠dp[i][j][x] = max(dp[i][j][x], dp[i - 1][x][y] + np[j]);}}}}ll ans = 0;//枚举第n层所有状态的最大值for (int i = 1; i < k; i++){for (int j = 1; j < k; j++){ans =max(ans,dp[n][i][j]);}}cout << ans << endl;
}