.NET Core容器化开发系列（一）——Docker里面跑个.NET Core

前言

博客园中已经有很多如何在Docker里面运行ASP.NET Core的介绍了。本篇主要介绍一些细节，帮助初学的朋友更加深入地理解如何在Docker中运行ASP.NET Core。

640?wx_fmt=png

安装Docker

Docker现支持在主流Linux、Windows和macOS上安装，官方的安装文档请参考docker docs。鉴于国内的网络环境，建议通过国内大厂/高校提供的镜像站快速安装，比如阿里巴巴开源镜像站，Ubuntu和Centos7上的安装方式如下：

Ubuntu 14.04 16.04 (使用apt-get进行安装)

# step 1: 安装必要的一些系统工具

sudo apt-get update

sudo apt-get -y install apt-transport-https ca-certificates curl software-properties-common

# step 2: 安装GPG证书

curl -fsSL http://mirrors.aliyun.com/docker-ce/linux/ubuntu/gpg | sudo apt-key add -

# Step 3: 写入软件源信息

sudo add-apt-repository "deb [arch=amd64] http://mirrors.aliyun.com/docker-ce/linux/ubuntu $(lsb_release -cs) stable"

# Step 4: 更新并安装 Docker-CE

sudo apt-get -y update

sudo apt-get -y install docker-ce

# 安装指定版本的Docker-CE:

# Step 1: 查找Docker-CE的版本:

# apt-cache madison docker-ce

#   docker-ce | 17.03.1~ce-0~ubuntu-xenial | http://mirrors.aliyun.com/docker-ce/linux/ubuntu xenial/stable amd64 Packages

#   docker-ce | 17.03.0~ce-0~ubuntu-xenial | http://mirrors.aliyun.com/docker-ce/linux/ubuntu xenial/stable amd64 Packages

# Step 2: 安装指定版本的Docker-CE: (VERSION 例如上面的 17.03.1~ce-0~ubuntu-xenial)

# sudo apt-get -y install docker-ce=[VERSION]

CentOS 7 (使用yum进行安装)

# step 1: 安装必要的一些系统工具

sudo yum install -y yum-utils device-mapper-persistent-data lvm2

# Step 2: 添加软件源信息

sudo yum-config-manager --add-repo http://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo

# Step 3: 更新并安装 Docker-CE

sudo yum makecache fast

sudo yum -y install docker-ce

# Step 4: 开启Docker服务

sudo systemctl enable docker && systemctl start docker

# 注意：

# 官方软件源默认启用了最新的软件，您可以通过编辑软件源的方式获取各个版本的软件包。例如官方并没有将测试版本的软件源置为可用，你可以通过以下方式开启。同理可以开启各种测试版本等。

# vim /etc/yum.repos.d/docker-ce.repo

# 将 [docker-ce-test] 下方的 enabled=0 修改为 enabled=1

#

# 安装指定版本的Docker-CE:

# Step 1: 查找Docker-CE的版本:

# yum list docker-ce.x86_64 --showduplicates | sort -r

# Loading mirror speeds from cached hostfile

# Loaded plugins: branch, fastestmirror, langpacks

# docker-ce.x86_64 17.03.1.ce-1.el7.centos docker-ce-stable

# docker-ce.x86_64 17.03.1.ce-1.el7.centos @docker-ce-stable

# docker-ce.x86_64 17.03.0.ce-1.el7.centos docker-ce-stable

# Available Packages

# Step2 : 安装指定版本的Docker-CE: (VERSION 例如上面的 17.03.0.ce.1-1.el7.centos)

# sudo yum -y install docker-ce-[VERSION]

以下我的实验在Centos7中进行，其他系统基本类似。

安装完成后，可以看到最新Docker版本为18.09（2018年12月27日）

640?wx_fmt=png

效果0X01

既然Docker安装好了，也正常运行起来了，我们第一件事儿做的就是运行一下Demo，看看是个什么效果，微软将dotnet的Docker镜像都托管在Docker Hub上，我们可以打开Docker Hub的官方网站：https://hub.docker.com 并直接搜索dotnet，找到microsoft/dotnet即可。

根据Wiki提示，我们使用如下命令运行第一个ASP.NET Core的Demo：

docker run -it --rm -p 8000:80 --name aspnetcore_sample microsoft/dotnet-samples:aspnetapp

运行后输出：

[root@singleCentos7 ~]# docker run -it --rm -p 8000:80 --name aspnetcore_sample microsoft/dotnet-samples:aspnetapp

Unable to find image 'microsoft/dotnet-samples:aspnetapp' locally

aspnetapp: Pulling from microsoft/dotnet-samples

a5a6f2f73cd8: Pull complete

1e6f560accc2: Pull complete

8176b77dc10d: Pull complete

e21dd5015bb0: Pull complete

10a7ec297783: Pull complete

52c4b3af04fb: Pull complete

Digest: sha256:de388b1ced92eadb906f806d0253d93c76cb92b0814798e7441c014b9645a32c

Status: Downloaded newer image for microsoft/dotnet-samples:aspnetapp

warn: Microsoft.AspNetCore.DataProtection.KeyManagement.XmlKeyManager[35]

No XML encryptor configured. Key {024f9978-2fea-4d8e-818a-b9a378553244} may be persisted to storage in unencrypted form.

Hosting environment: Production

Content root path: /app

Now listening on: http://[::]:80

Application started. Press Ctrl+C to shut down.

简单解释一下命令中几个常见的参数：

-it 开启一个交互窗口，也急运行docker后，处于docker的交互式输入输出页面

--rm 当从运行的容器中退出（ctrl+c）时，删除镜像残留信息及数据

-p 端口映射，将宿主机端口映射到容器内端口

--name 给容器起个名字，如不设置该项，容器名称将有docker服务随机设定

最后是镜像的地址以及tag

运行该段命令后：

首先查询宿主机本地是否存在microsoft/dotnet-samples:aspnetapp镜像

如不存在，则从远端拉取镜像

拉取成功后，运行指定命令，将Demo服务运行起来

此时我们在局域网的任意一台电脑浏览器中输入http://[宿主机IP]:8000 即可打开容器运行的demo

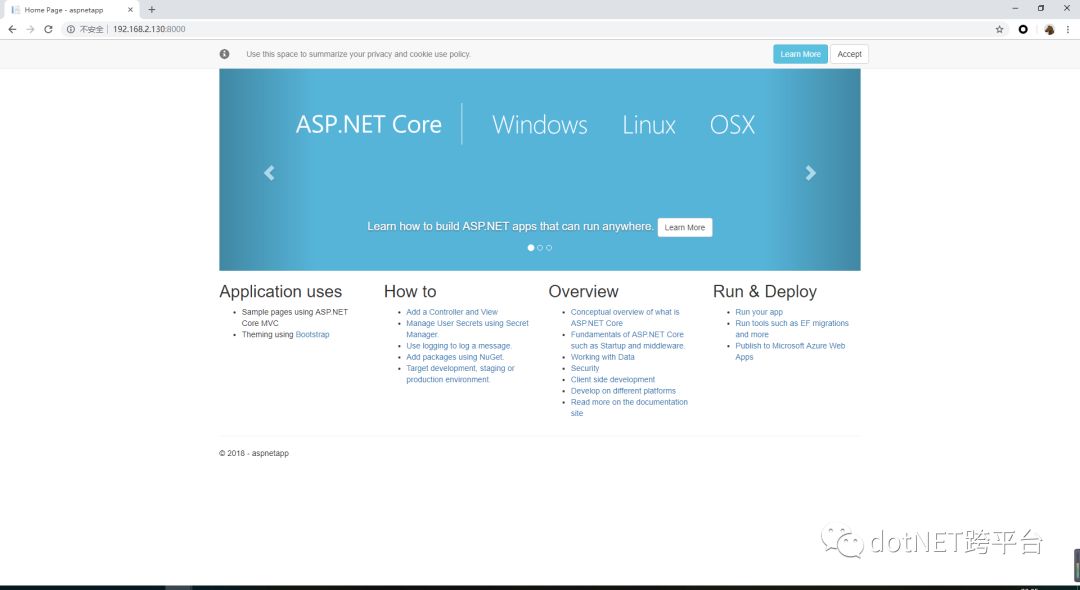
640?wx_fmt=png

效果0X02

看完官方的Demo，接下来我们自制一个DemoV2 。该思路采用将Docker容器转制为镜像的办法，因该方法扩展性不强，不适合重复使用，因此不被推荐，但其中的部分思路非常适合借鉴学习：

1	`docker run -it --rm` `--name dotnet_sdk microsoft/dotnet:sdk`

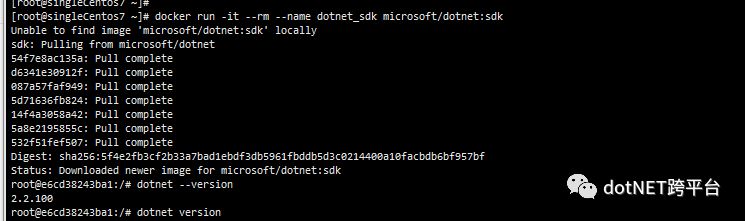
640?wx_fmt=png

接下来我们在tmp目录下新建一个ASP.NET Core MVC项目，并发布该项目都/app目录下

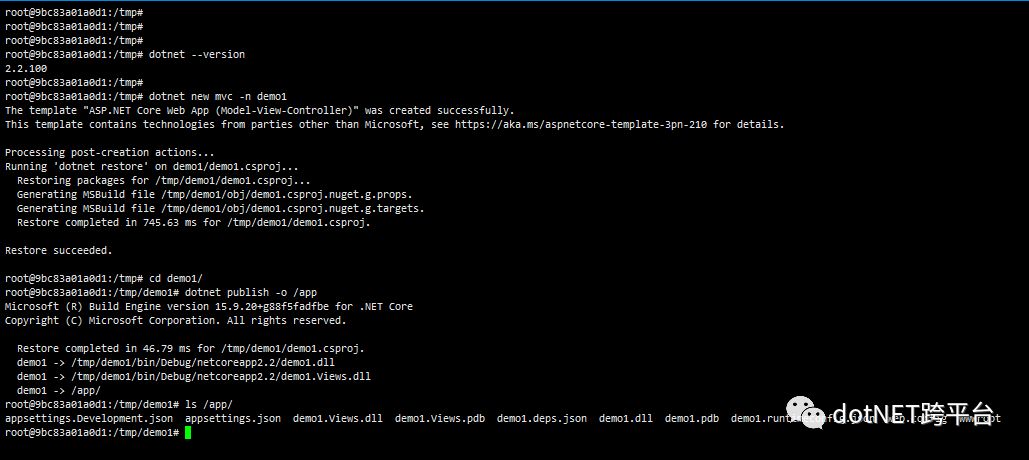
640?wx_fmt=png

此时我们进入/app目录后,执行命令，即可看到demo1已经能在容器中正常运行：

1	`cd` `/app` `&& dotnet demo1.dll`

接下来我们使用docker commit命令将当期容器转制为镜像，以便于我们重复使用。

首先，新开一个宿主机终端，并在终端中查看当期运行的容器：

1	`docker` `ps`

640?wx_fmt=png

可以发现名称为dotnet_sdk的容器，其容器Id为9bc83a01a0d1，此时执行如下命令：

1	`docker commit 9bc83a01a0d1 mydemo:v1`

即可将指定容器保存为名称为mydemo的镜像，执行docker images查看：

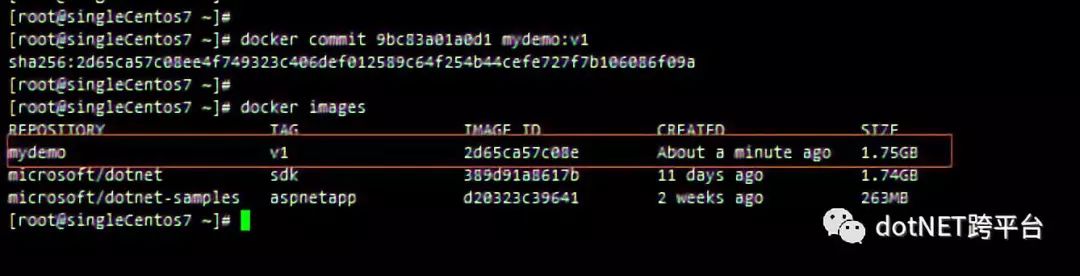
640?wx_fmt=jpeg

包含我们demo程序的镜像就已经保存下来了，接下来我们可以直接运行该镜像查看效果：

docker run -it --rm -p 8001:80 --name ggg mydemo:v1 sh -c "cd /app && dotnet demo1.dll"

640?wx_fmt=png

打开浏览器访问效果：

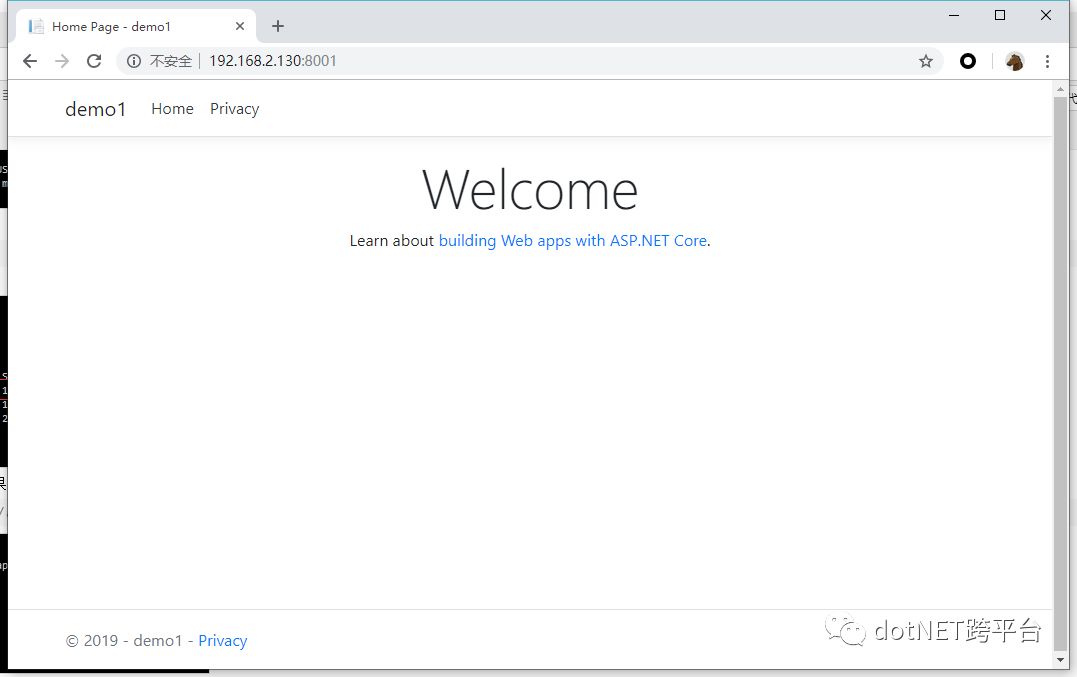
640?wx_fmt=png

效果0x03

接下来我们用最常见也是最合适的方式制作我们的.NET Core MVC镜像---Dockerfile

如果我们希望在Linux下直接开始.NET Core的代码编写，首先就必须要安装平台相关的.Net Core SDK，安装完成后，才可以使用dotnet 的相关指令创建、编译、发布项目。此时我们可以在Docker下采取更“鸡贼”一些的办法：

首先，我们运行一个.Net Sdk的容器，并进入交互式界面：

docker run -it --rm --name dotnet_sdk -v /tmp/src:/tmp/src microsoft/dotnet:sdk

运行.Net Core最新的SDK，并将宿主机/tmp/src 文件夹挂在到容器/tmp/src下面，而后我们在这个文件夹的文件都不会因容器销毁二丢失。

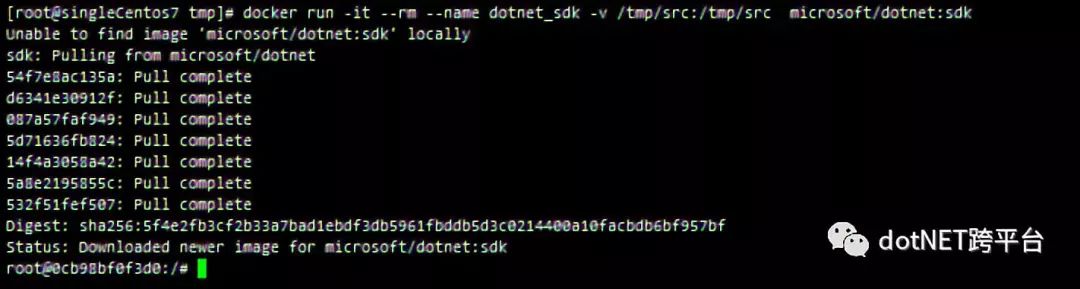
640?wx_fmt=jpeg

查看容器中dotnet版本信息，并在容器的/tmp/src文件夹下创建新的ASP.NET Core MVC项目：

cd /tmp/src

dotnet new mvc -n mydemo

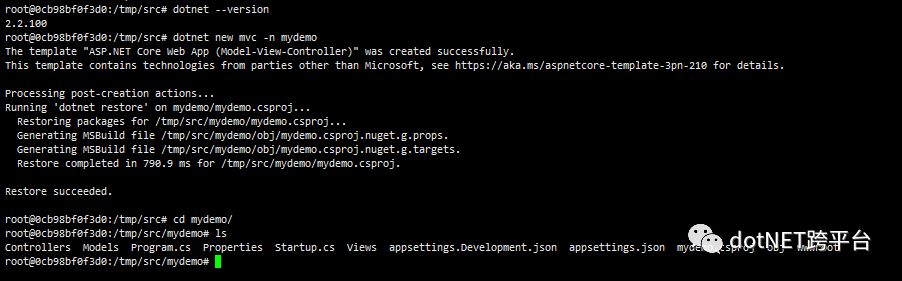
640?wx_fmt=png

此时可以退出当前容器了，接下来进入的是Docker的打包步骤。

虽然这种做法有点“画蛇添足”，但在某些时刻还是挺有用的，比如系统中存在老版本的.NET Core SDK，安装新版本的SDK可能会产生未知的问题，此时在Docker里面瞎玩，随便搞都没问题，棒呆！

同时有必要再强调一下，Docker从17.05版本开始支持“多阶段构建（multi-stages builds）”，而大多数干净的Linux操作系统在直接使用系统包管理器安装docker时安装的是13.1的版本Docker，是不支持该特性的。

下面介绍的模式是分层结构的构建方式。

在宿主机/tmp/src/mydemo下新建Dockerfile文件，输入以下内容：

FROM microsoft/dotnet:2.2-runtime AS base

WORKDIR /app

EXPOSE 80

FROM microsoft/dotnet:2.2-sdk AS publish

WORKDIR /src

COPY . .

RUN dotnet publish -c Release -o /app

FROM base AS final

WORKDIR /app

COPY --from=publish /app .

ENTRYPOINT ["dotnet", "mydemo.dll"]

该脚本一共分3次，第一次定义了基础镜像，并设置/app为基础工作目录，告知外部80为开放端口

第二次，将当期目录下的所有文件发送给Docker服务，执行发布过程，将发布输出到/app文件夹下

第三次，采用第一次的镜像基础作为当期镜像，并将第二次发布输出拷贝到当前基础工作目录/app

最后设置工作入口，当镜像运行时，执行dotnet mydemo.dll

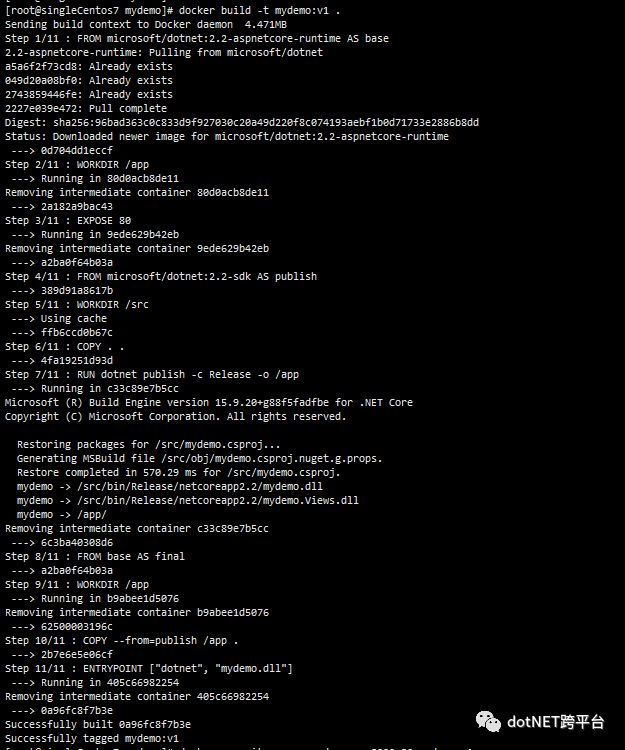
640?wx_fmt=png

通过docker images命令可以看到刚刚打包出的镜像

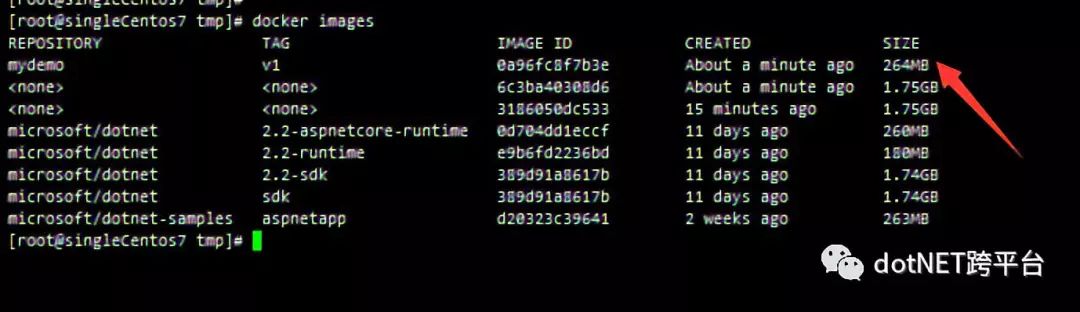
640?wx_fmt=jpeg

接下来我们尝试将镜像运行起来：

1	`docker run -it --name mydemo -p 8002:80 mydemo:v1`

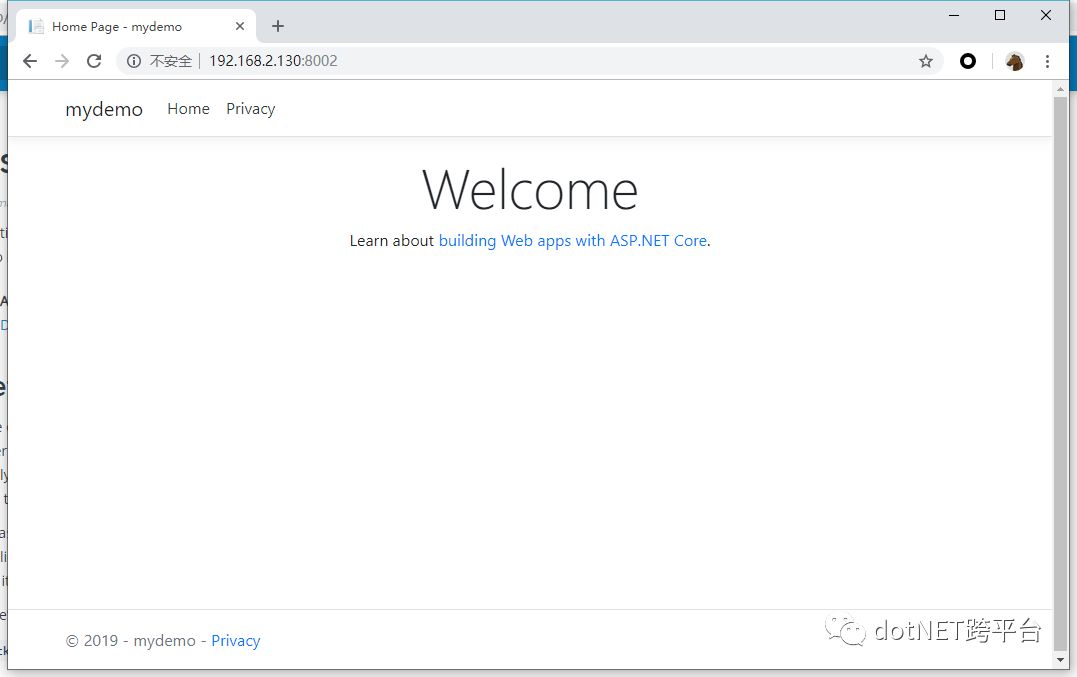
640?wx_fmt=png

成功！

这次随笔主要介绍了在Docker里面如何运行一个.NET Core项目的Demo，建议大家在学习Docker时，对如何书写Dockerfile多下点功夫，理解里面的基础命令关键词。

搭建基于Docker社区版的Kubernetes本地集群
Docker最全教程——从理论到实战（一）
Docker最全教程——从理论到实战（二）
Docker最全教程——从理论到实战（三）
Docker最全教程——从理论到实战（四）
Docker最全教程——从理论到实战（五）
Docker最全教程——从理论到实战（六）
Docker最全教程——从理论到实战（七）
Docker最全教程——从理论到实战(八)
Docker最全教程——从理论到实战（九）
Asp.Net Core + Docker 搭建
dotnet core调试docker下生成的dump文件
为什么是容器，Docker和Kubernetes?
把ABP框架部署到Docker中
实战中的asp.net core结合Consul集群&Docker实现服务治理

原文地址:https://www.cnblogs.com/leafly/p/10188159.html

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com

640?wx_fmt=jpeg