介绍

 

微服务中有关键的几项技术，其中网关和服务服务发现，服务注册相辅相成。

首先解释几个本次教程中需要的术语

网关 Gateway（API GW / API 网关），顾名思义，是企业 IT 在系统边界上提供给外部访问内部接口服务的统一入口，简化了外部由于多服务协同完成任务时的繁琐配置。网关组件有Kong，ocelot,

服务发现：通过网关访问内部各个微服务，网关要找到所需服务的过程称为服务发现

服务注册：既然有服务发现，前提是要把所需服务提前“录入”，这个录入的过程称为服务注册。服务注册可配置文件（人肉方式不推荐），也可用服务注册组件如Consul或者Eureka等等（推荐）

搭建Consul集群(Windows)

官网下载Consul程序，https://www.consul.io/downloads.html

下载下来就是一个可执行文件Consul.exe

Consul有两种代理模式，一种server,一种client,官方建议Server端达到3台以上才可高可用，但不要太多，太多会给集群间数据同步造成压力，client数量不限。

多个server端之间会选择出一个leader,当一个server的leader宕机则会从其他server端”投票“选择新的leader

实践

这里server我们用2台实验

192.168.74.55

192.168.74.54

1台Client

192.168.74.161

consul启动有两种方式一种是命令行，一种是配置文件的方式。

命令行方式启动一个consul的server端

consul agent -server -ui -bootstrap-expect 2 -data-dir opt/consul/data -node ServerMaster -bind 192.168.74.55 -client 192.168.74.55

关键参数说明

-server：server模式启动

-ui ：开启ui界面（consul.exe内部带了GUI图形界面操作）

 -bootstrap-expect 2：server端到2个时集群生效

-data-dir：consul产生的文件路径（consul自己会产生一下数据存储的位置）

-node：此节点名称

-bind：集群内部通信地址，默认0.0.0.0

-client：此节点绑定的通讯地址

以上只是关键参数，以下是完整参数说明：  

 

但是命令启动很繁琐，所以推荐下面的配置文件的方式启动

在consul同文件夹下建立一个server.json的配置文件

 

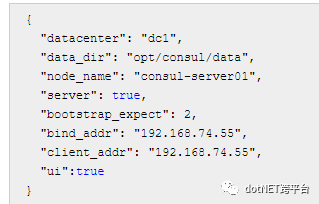
为了快速启动，再建立一个bat批处理文件runconsul.bat

consul agent -config-dir server.jsonpause

双击runconsul.bat启动consul

在192.168.74.54服务器开启一个server端继续以上操作。

命令方式启动

consul agent -server -ui -data-dir opt/consul/data -node Server01 -bind 192.168.74.54 -client 192.168.74.54 -join=192.168.74.55

-join将192.168.74.54加入到192.168.74.55服务器

配置文件方式：

 

在192.168.74.161服务器开启一个consul的client端

命令方式：

consul agent -ui -data-dir opt/consul/data -node ServerSlave  -bind 192.168.74.161 -client 192.168.74.161 -join 192.168.74.55

配置文件方式：

效果 

简单Consul集群到这里就搭建成功，只要访问三台服务器任意一个都可数据同步，演示：

 

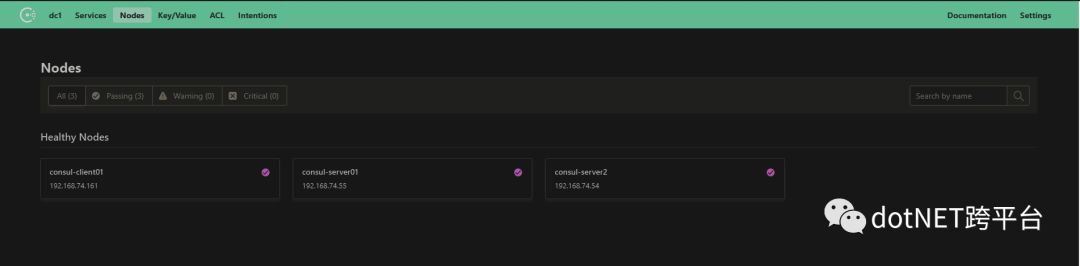
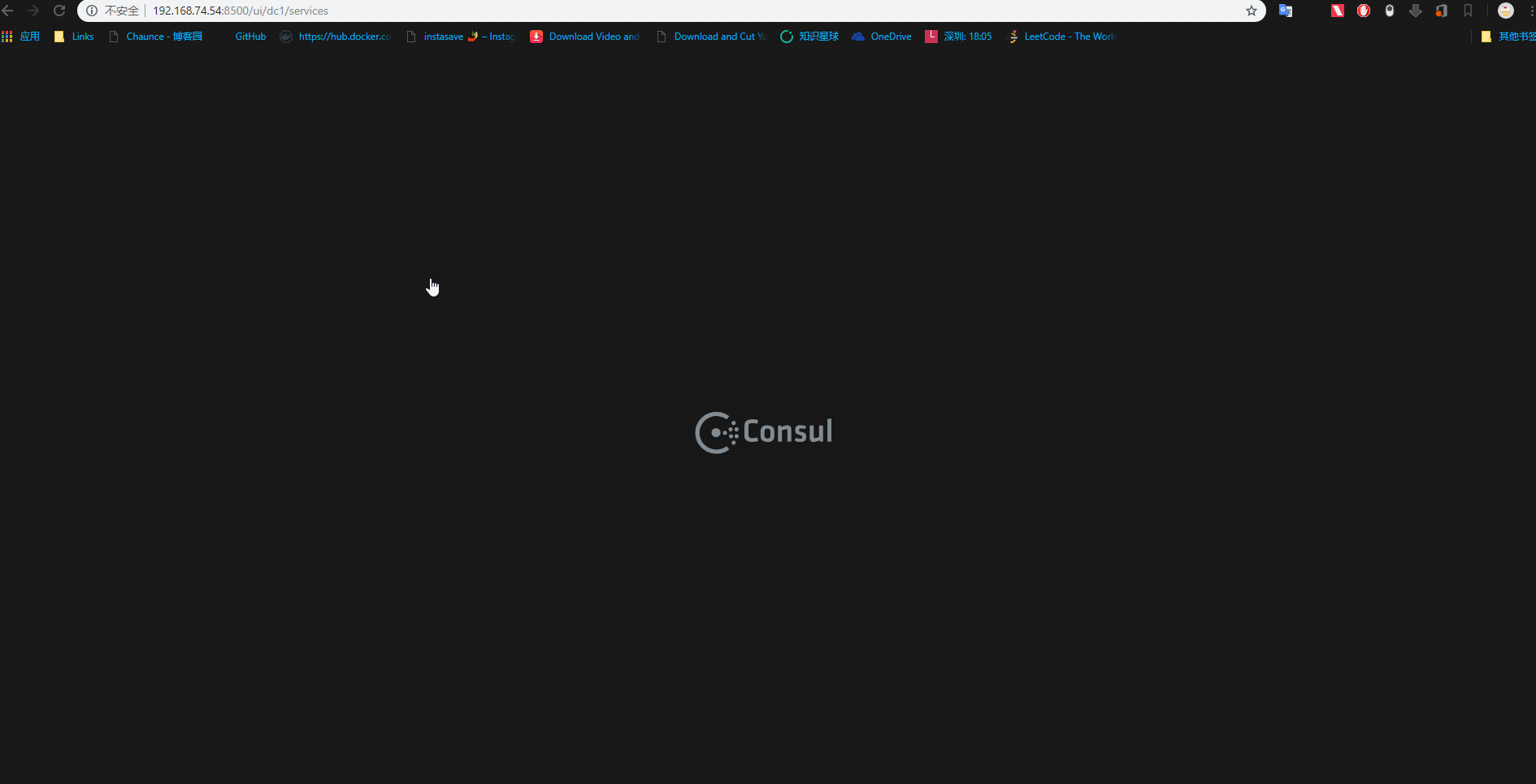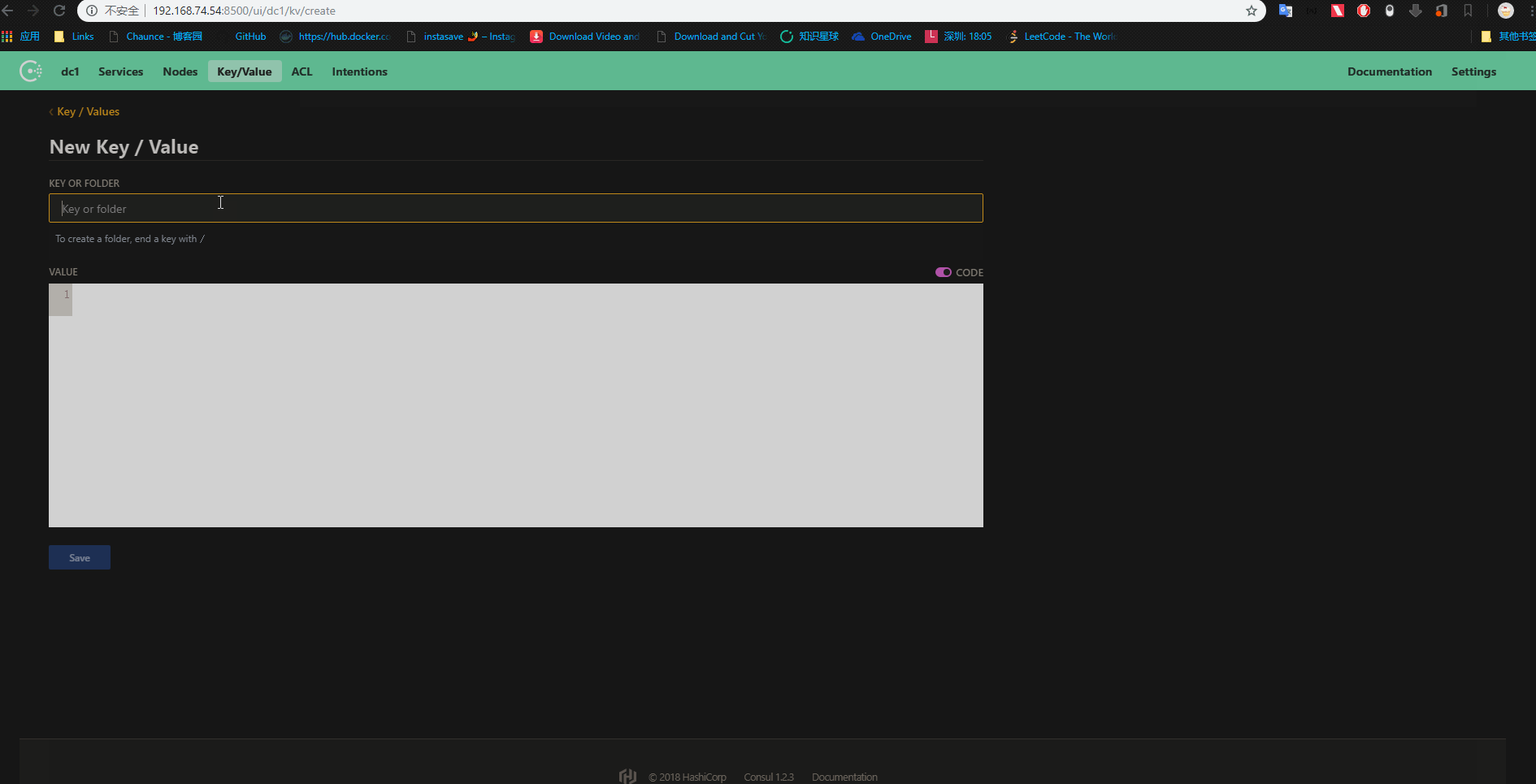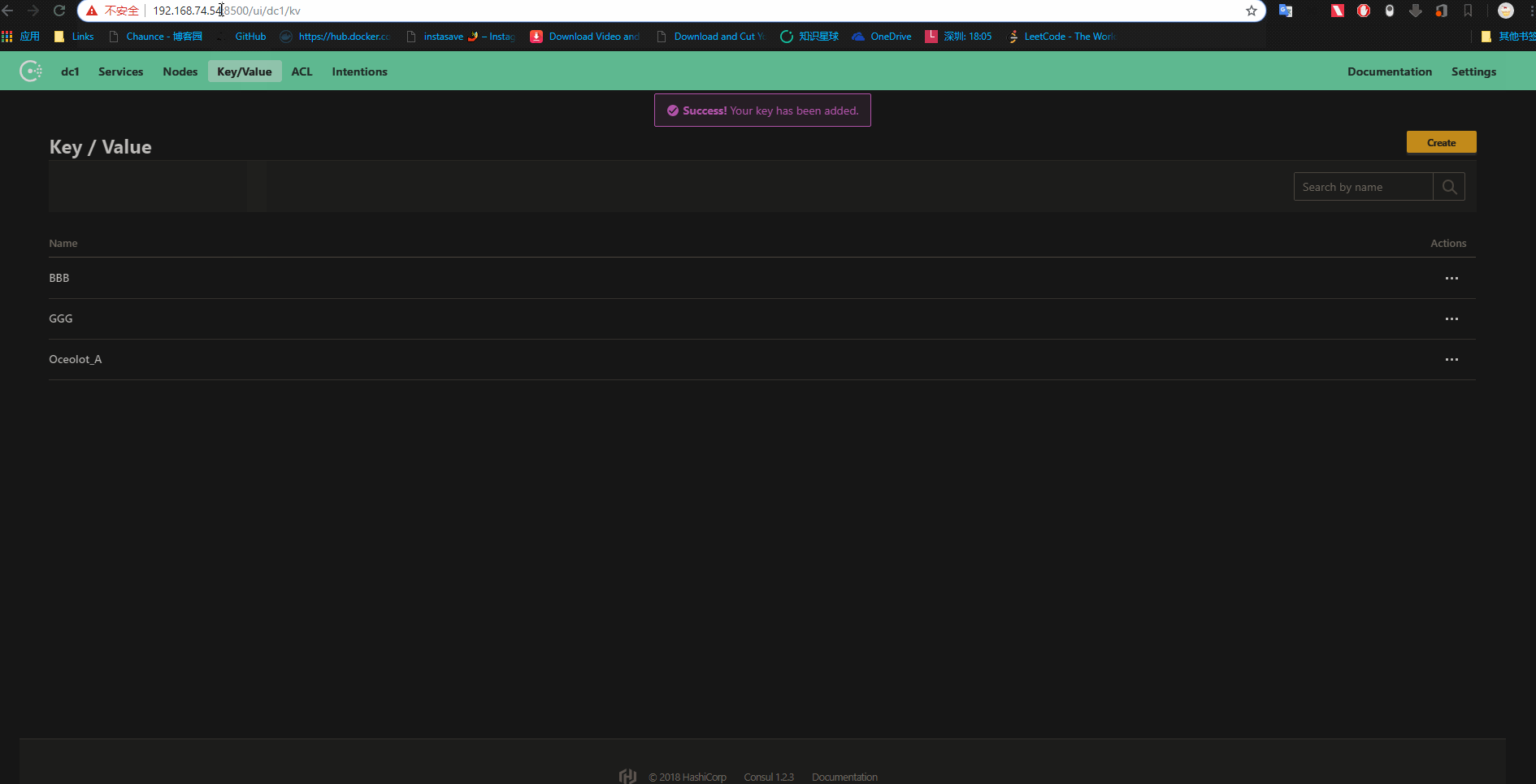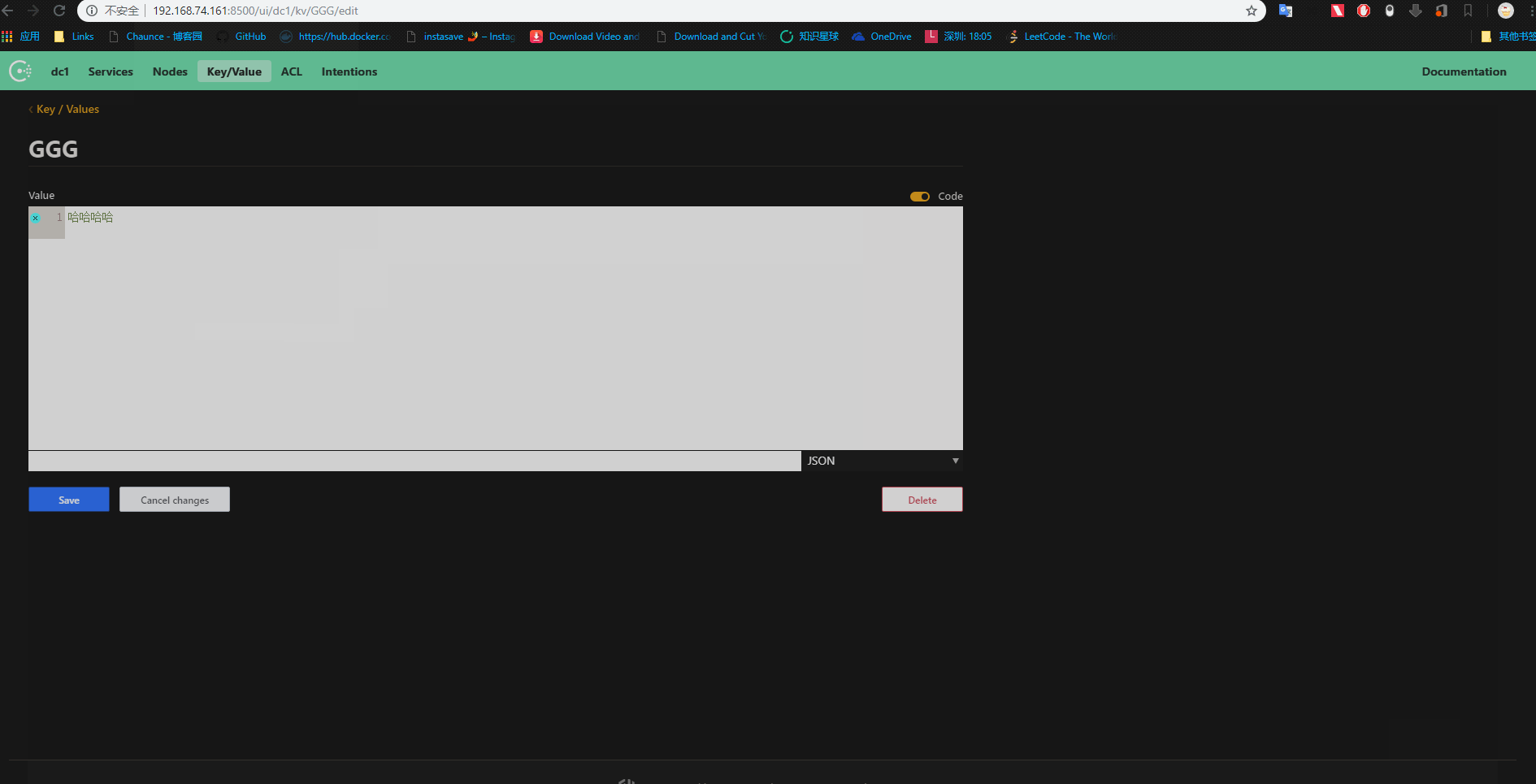
 netcore集成Consul服务注册

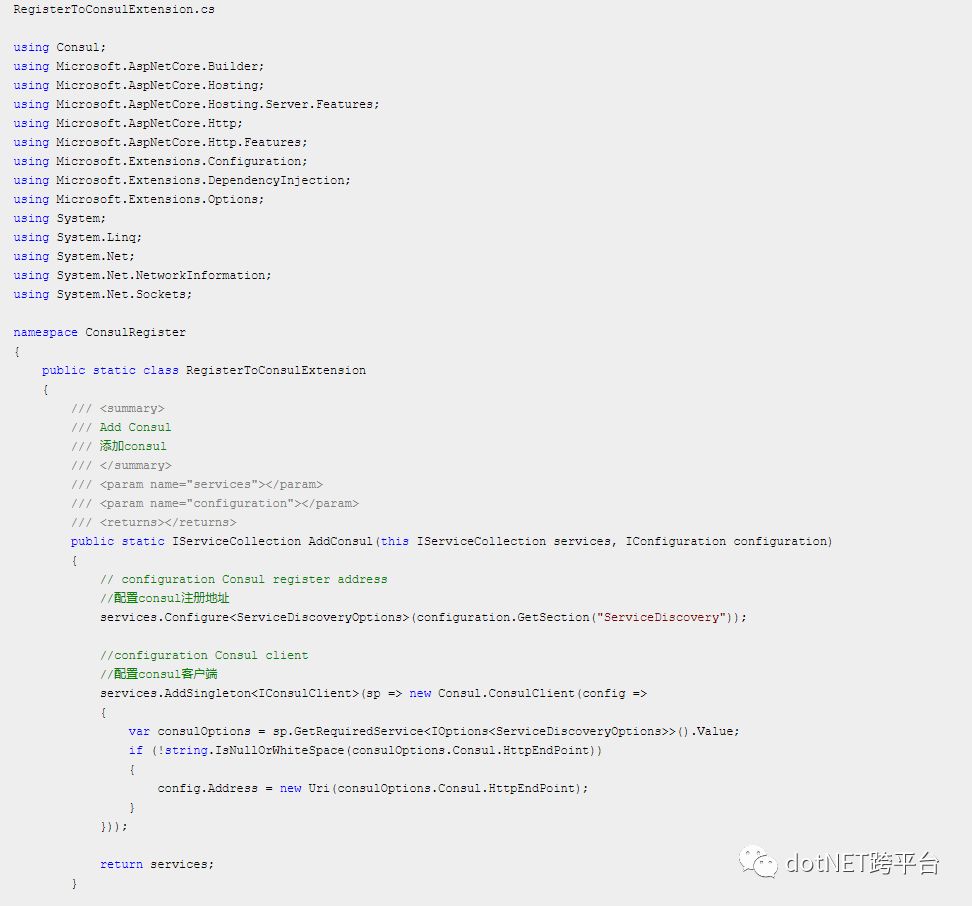
服务注册关键代码

首先新建一个ConsulClient的类库

 

ConsulRegister.csproj所需组件如下：

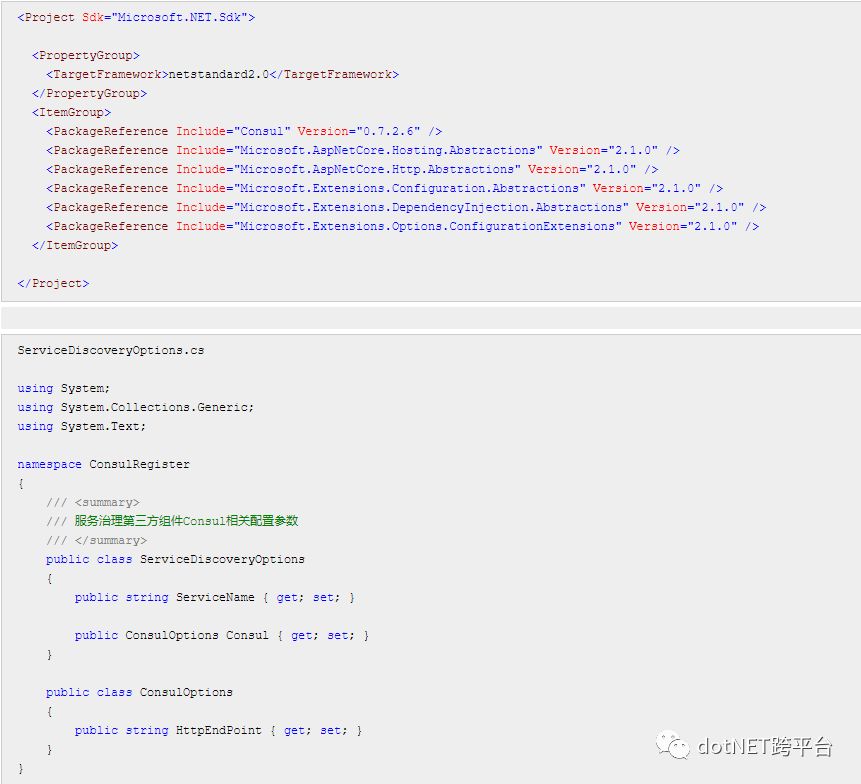
再新建一个.netcore的webapi项目WebA，并且引用ConsulRegister项目

在WebA项目中的Startup.cs文件中加入Consul服务

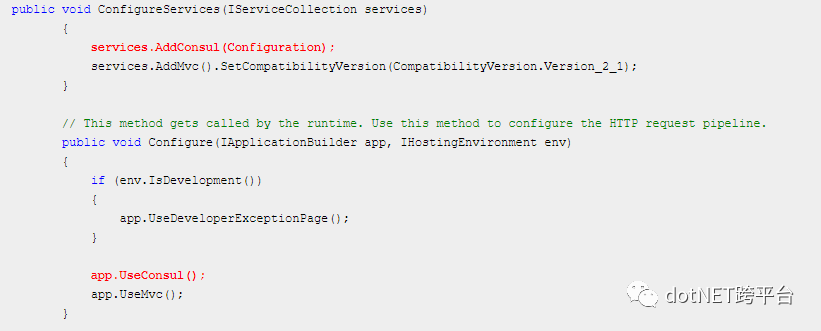
在WebA项目的appsettings.json配置文件中加入以下Consul服务端配置

这里服务注册就算完成

Ocelot网关搭建

接下来继续Ocelot借助于Consul实现服务发现

新建项目Ocelot.Gateway

将以下依赖加入Ocelot.Gateway.csproj中：

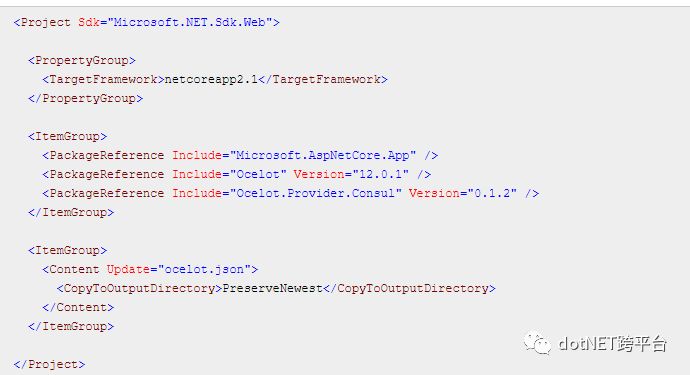
新建ocelot.json文件

修改Startup.cs文件如下：

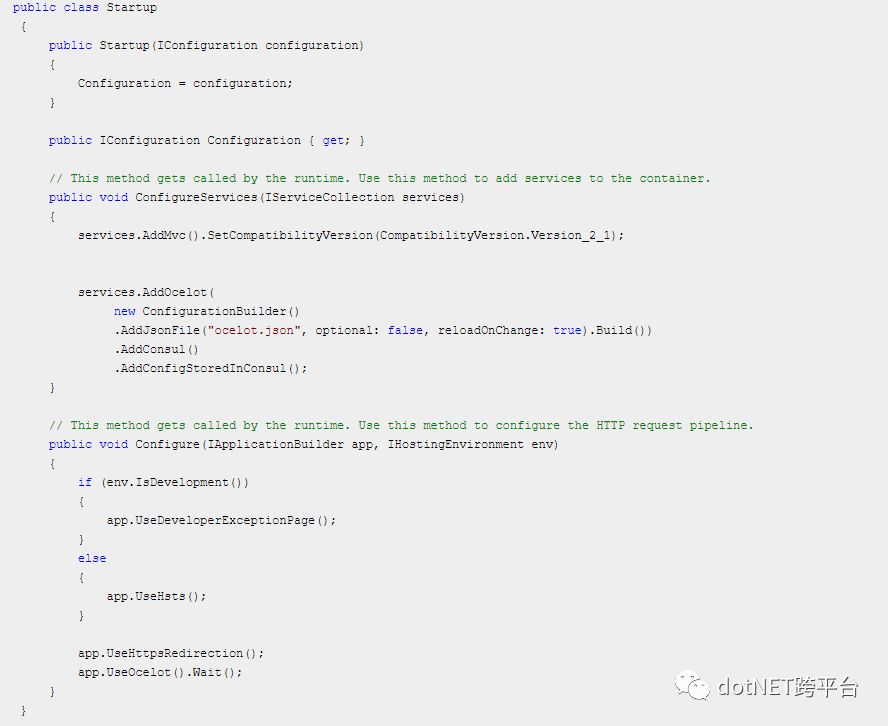
发布WebA后复制两份分别启动

dotnet WebA.dll --urls="http://0.0.0.0:2001"

dotnet WebA.dll --urls="http://0.0.0.0:2002"

到这里相当于2001和2002程序简单集群了一下

可以发现日志中有 http://192.168.74.161:2002/HealthCheck调用信息：

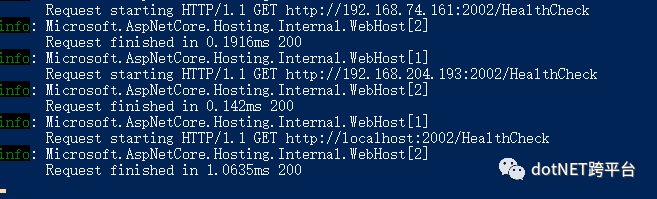
这其实是consul进行健康检查进行的调用。

启动多个程序后，打开浏览器打开Consuld界面会发现注册了两个服务

 

 

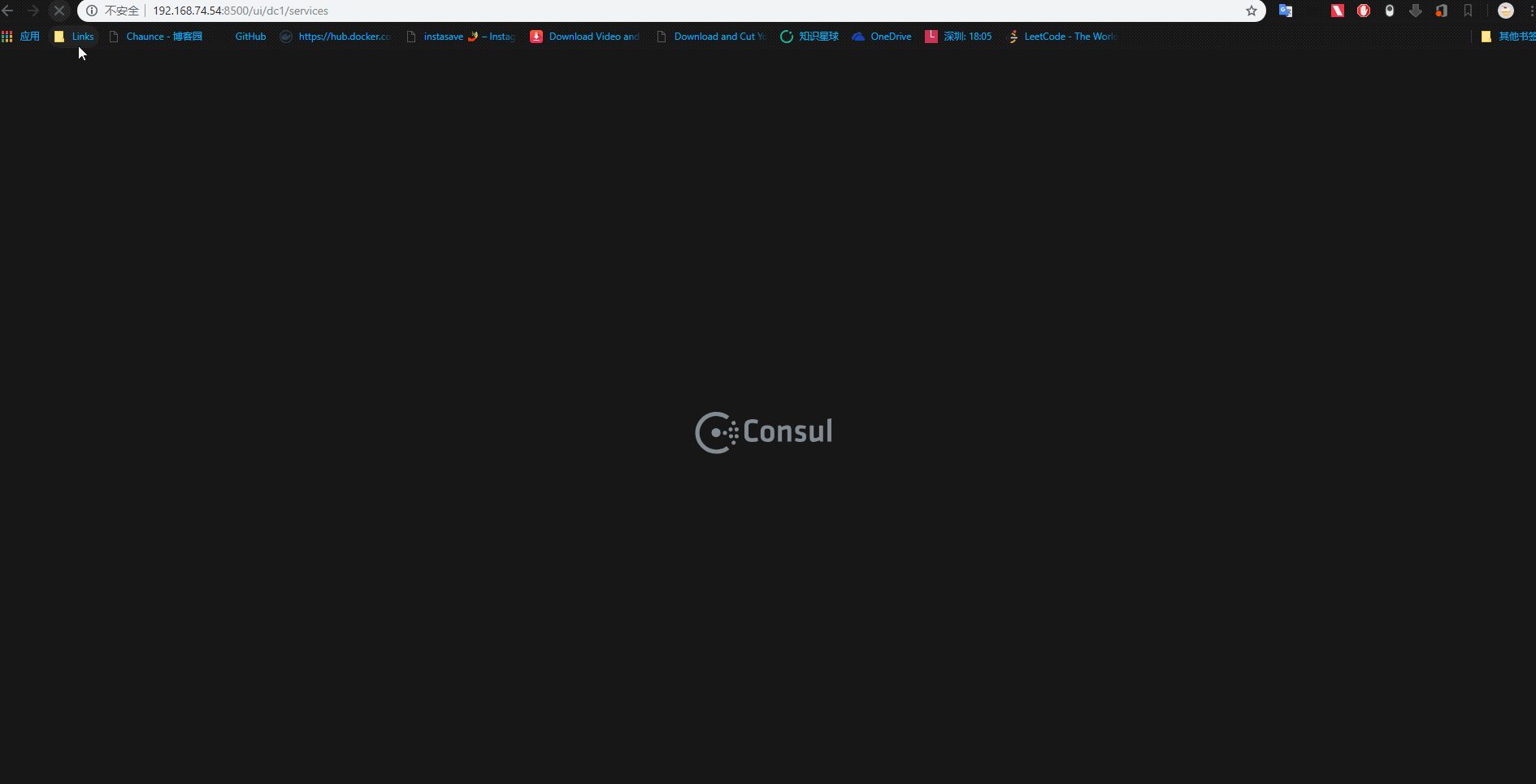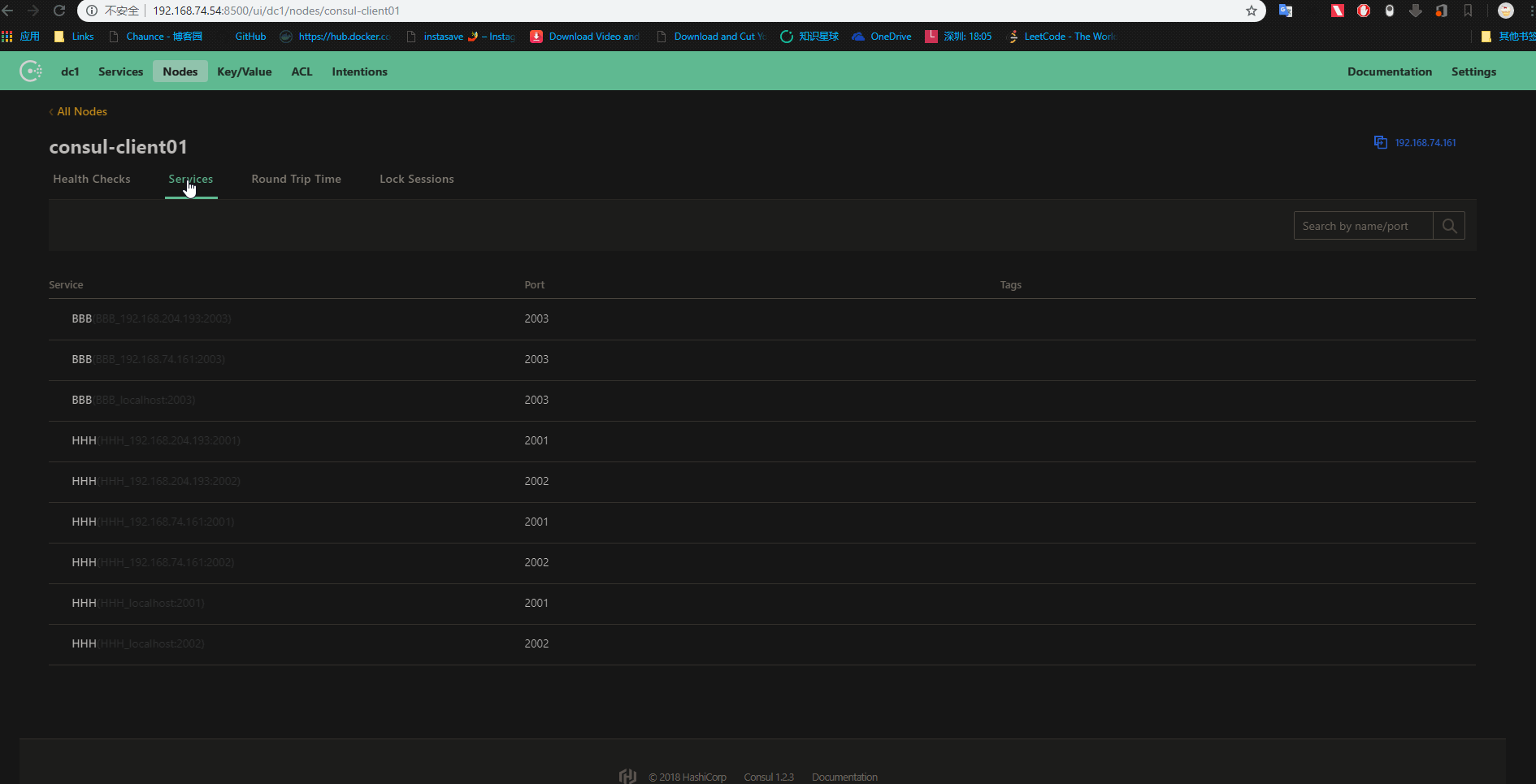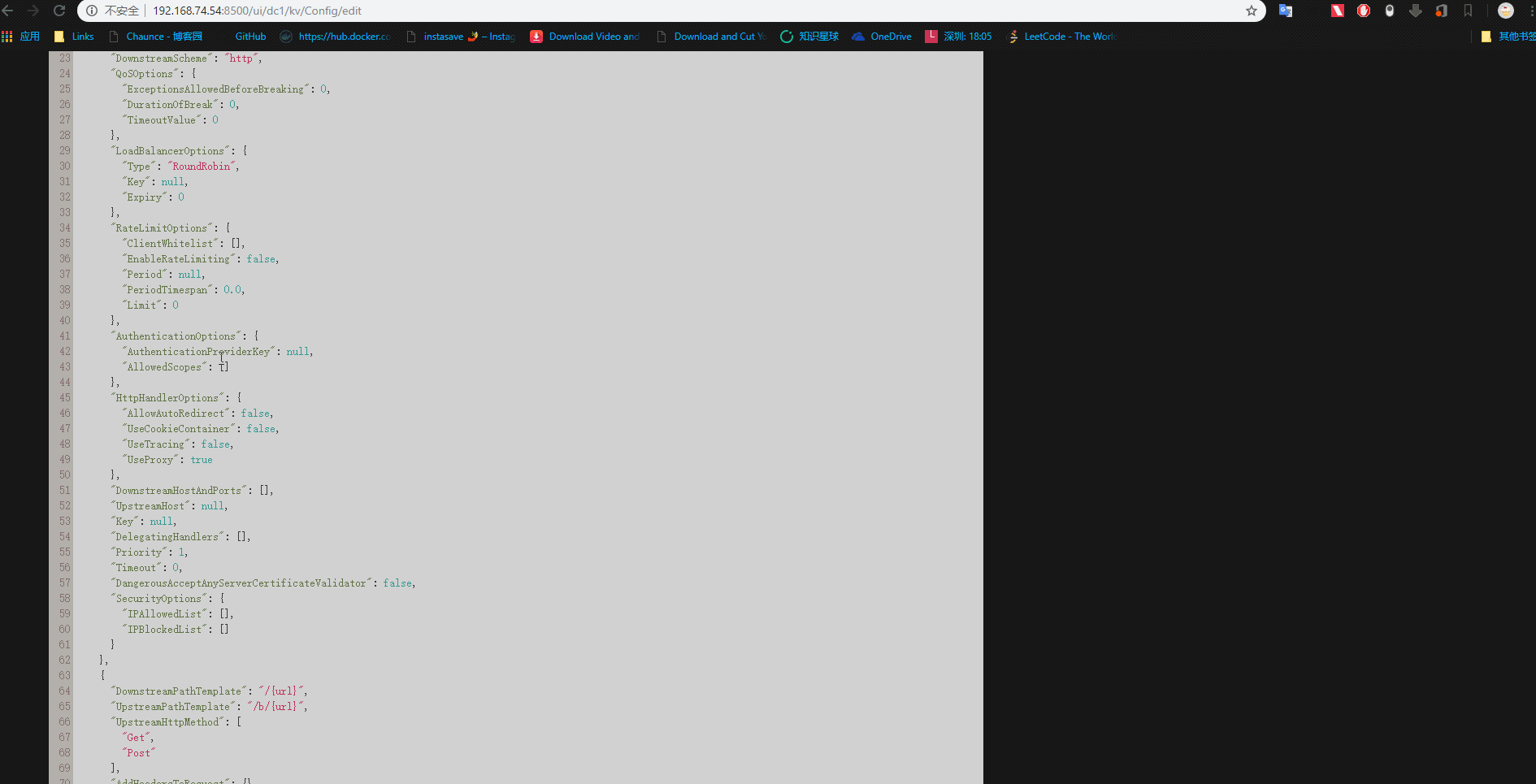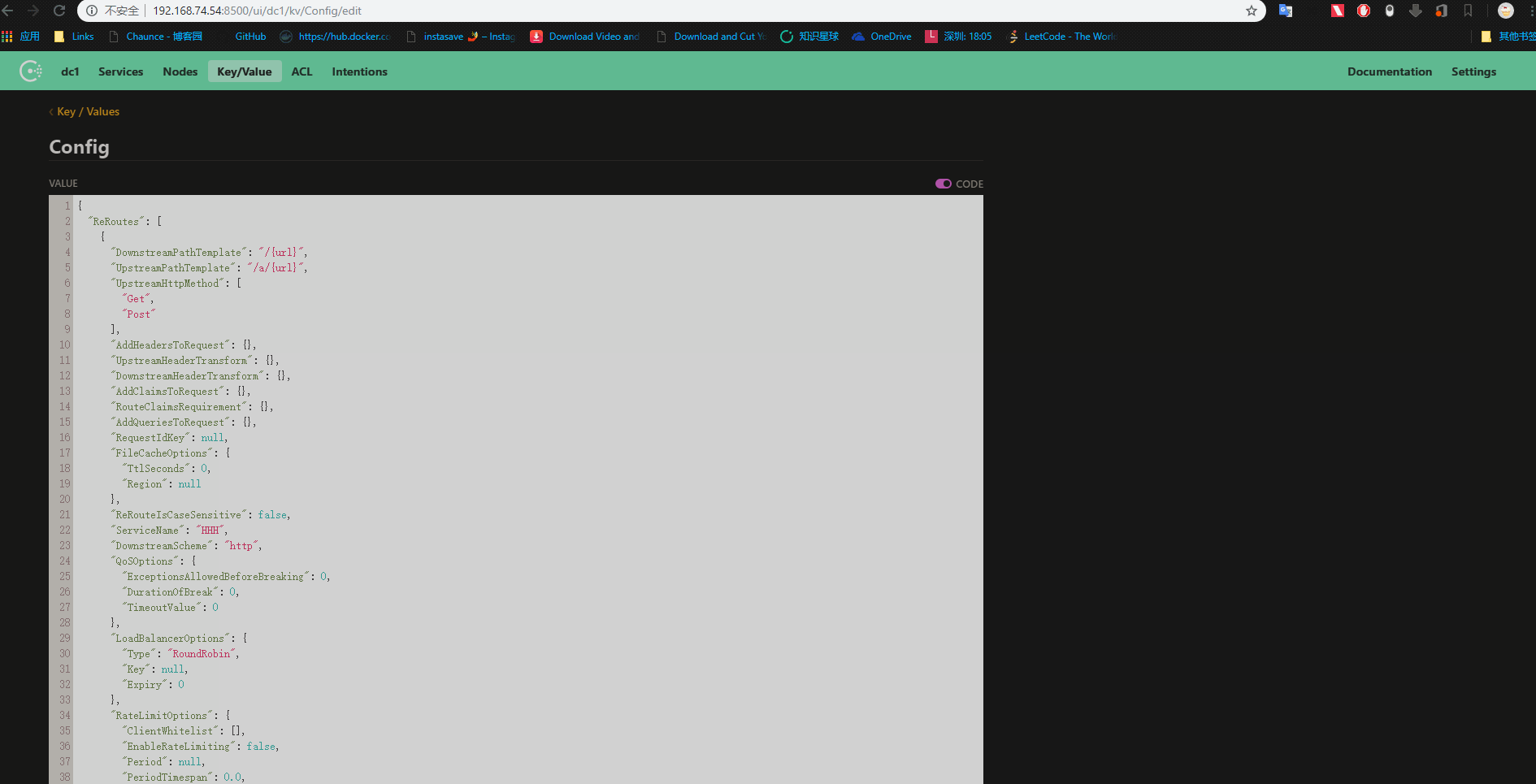
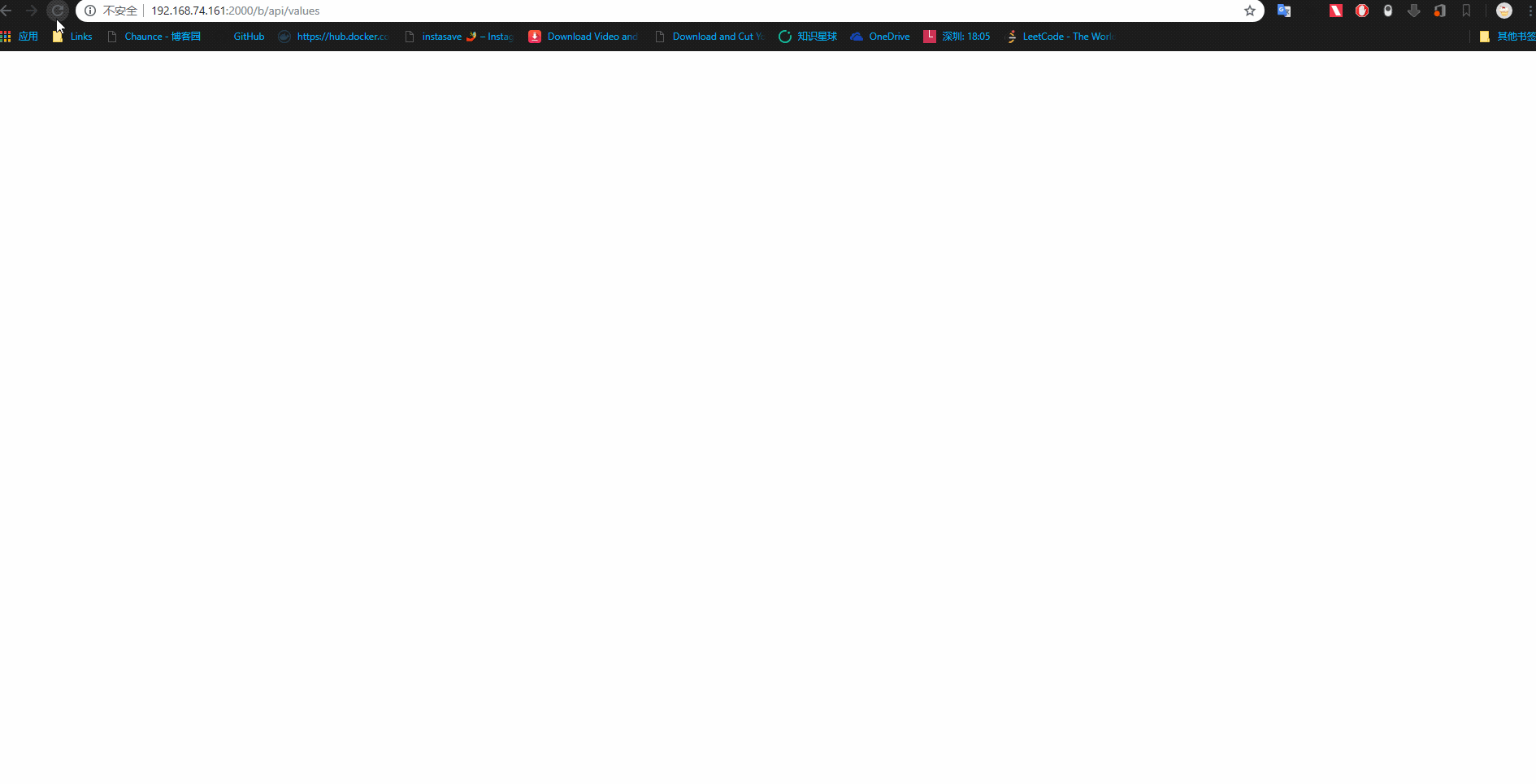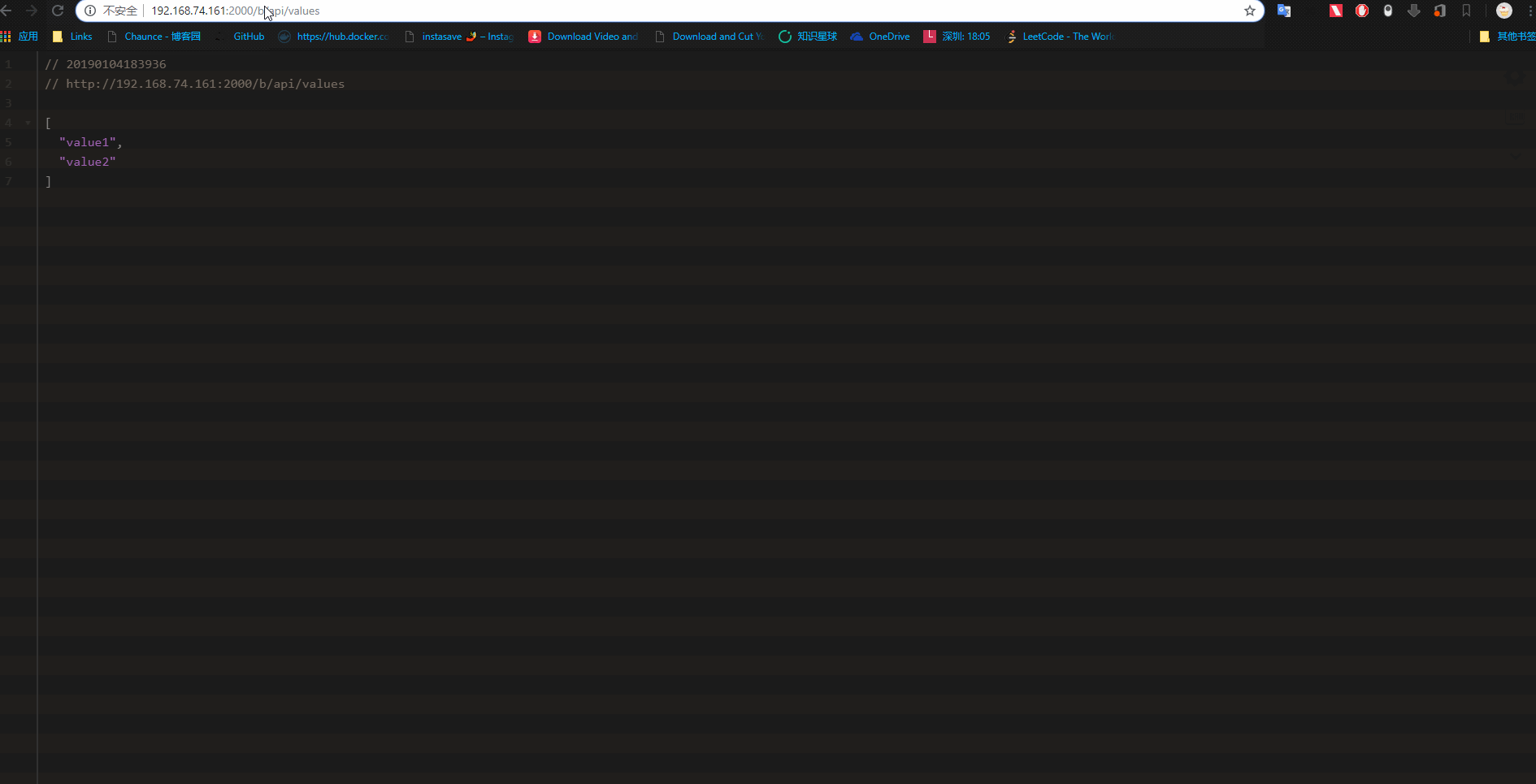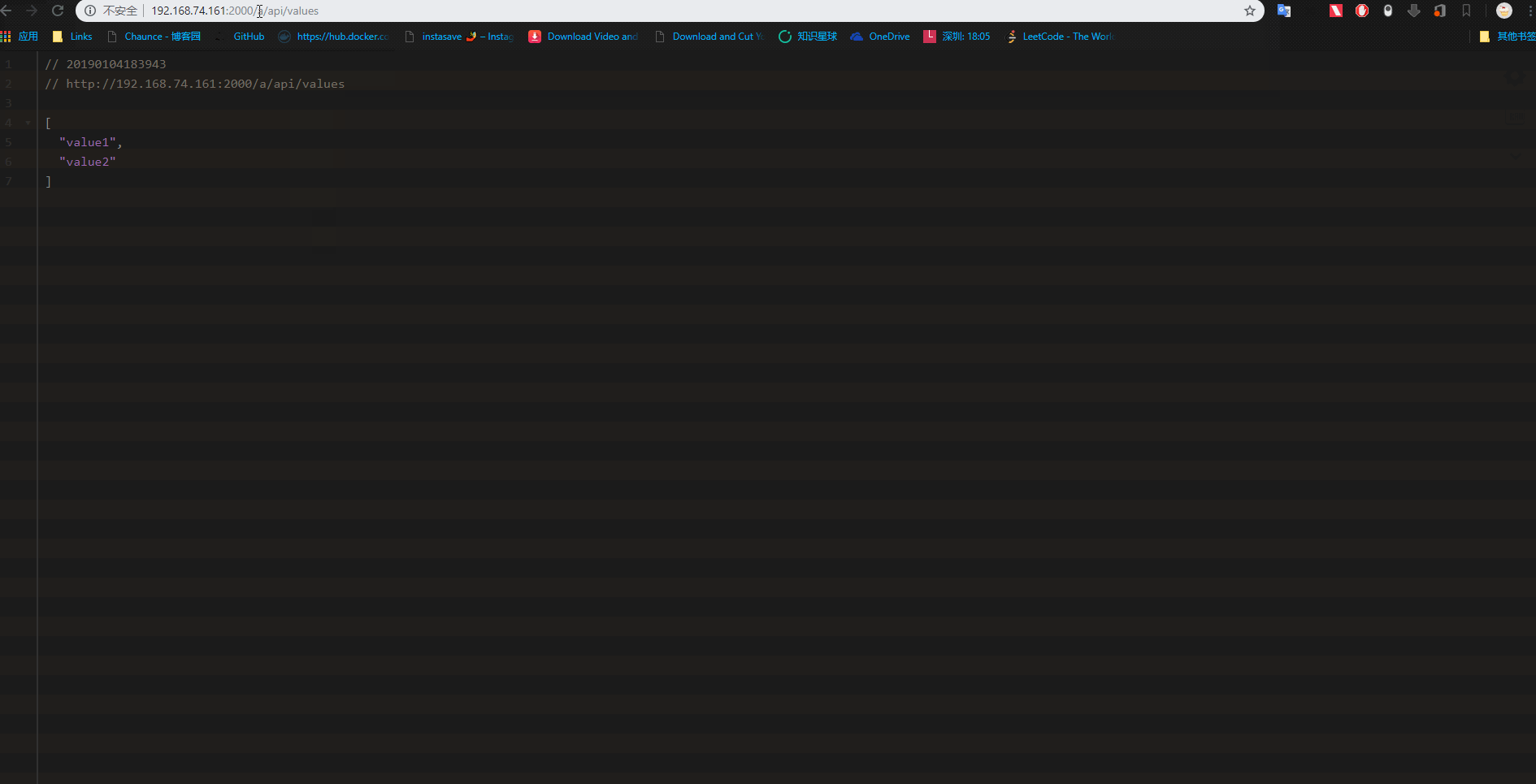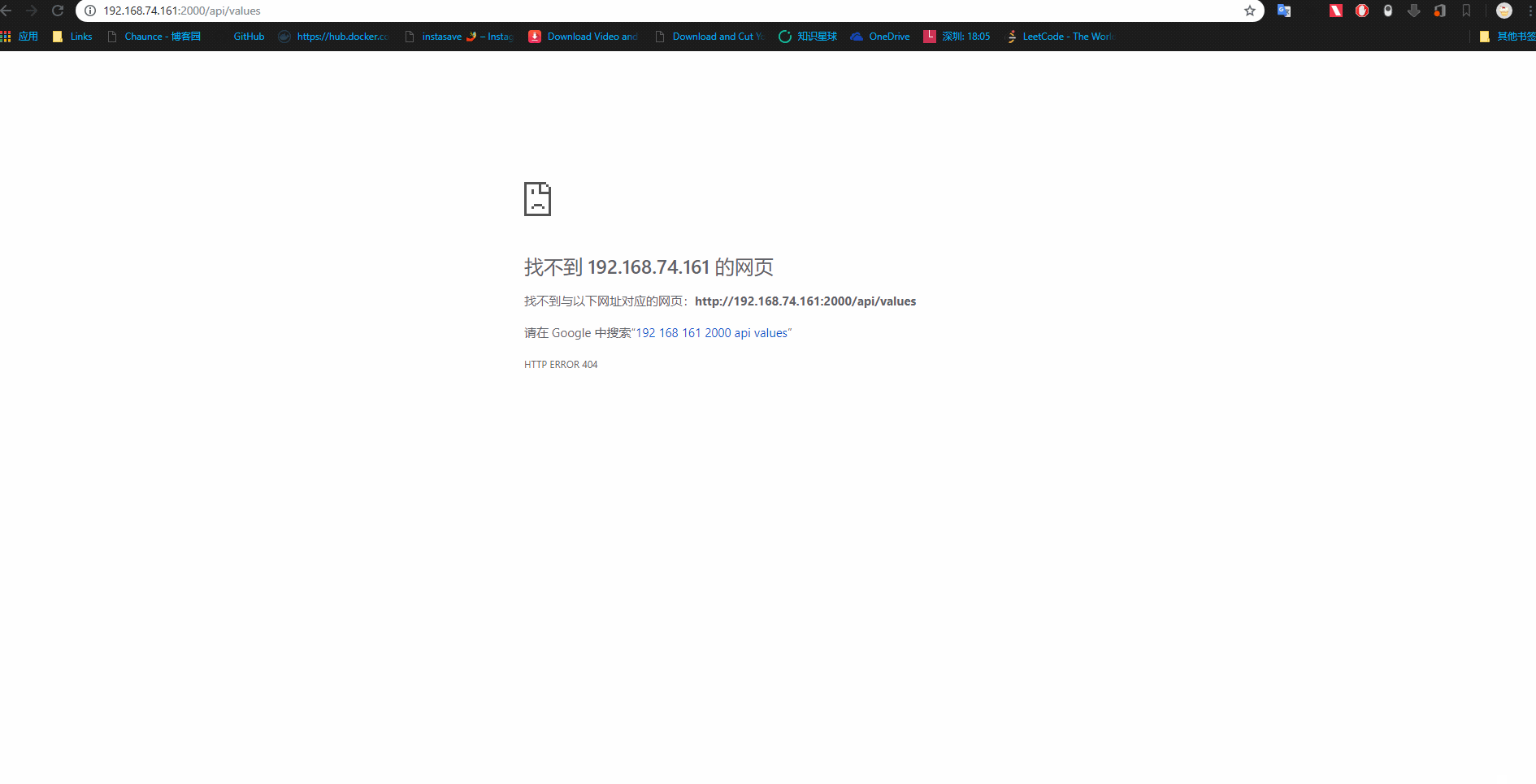
这里ocelot网关和consul的服务注册和发现就算初步集成。

如果生成环境是windows的情况，将consul做成windwos服务即可

sc create "ConsulServer" binPath="F:\XXX\consul.exe agent -config-dir XXX.json"

生产环境是linux则借助systemd做成守护进程即可 

目前集群搭建成功，但是连接的话如果指定某个端点的ip进行连接，端点宕机，就会导致网关一样无法连接consul进行服务发现。所以还需进行配置暴露一个端点让客户端连接，配置详情：https://www.consul.io/docs/connect/configuration.html

不过也可以做成虚拟ip进行多台consul的负载。客户端连接虚拟ip即可

项目地址：

https://github.com/liuyl1992/Ocelot.GatewayToConsul

原文地址:https://www.cnblogs.com/xiaoliangge/p/10221950.html

---

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com