素数

solution

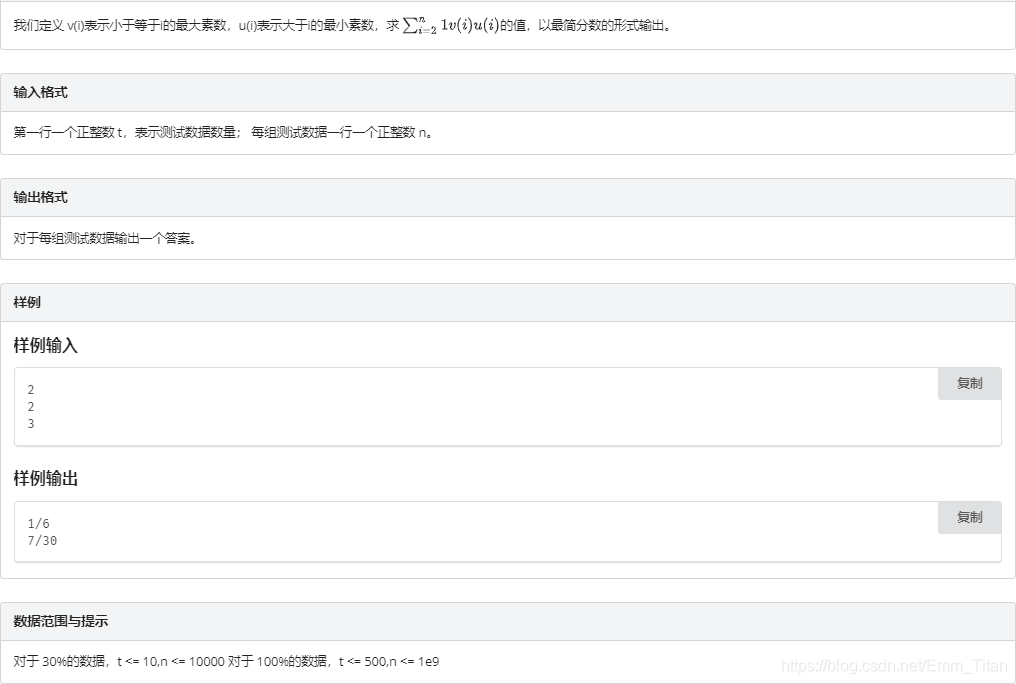
通过观察可得一个结论
对于两个相邻的质数$p_1,p_2(p_1<p_2)$
对于$x\in [p_1,p_2)$，都有$u_x=p_2,v_x=p_1$

接着随随便便推一下
假设三个相邻的质数$p_1,p_2,p_3(p_1<p_2<p_3)$
对于$x_1\in [p_1,p_2)$👉${\sum }_{x_1}=(p_2-p_1)\ast \frac{1}{p_1\ast p_2}$
对于$x_2\in [p_2,p_3)$👉${\sum }_{x_2}=(p_3-p_2)\ast \frac{1}{p_2\ast p_3}$
将两式相加👉${\sum }_{x_i\in [p_1,p_3)}\frac{1}{u_{x_i}\ast v_{x_i}}=\frac{p_3\ast (p_2-p_1)+p_1\ast (p_3-p_2)}{p_1\ast p_2\ast p_3}=\frac{p_3-p_1}{p_1\ast p_3}$
按道理下面继续相加$p_3,p_4...p_i$都会被消掉，只剩下第一个质数$2$和最后一个小于等于$n$的质数
于是就又出来了一个结论
只不过最后那个质数和$n$之间的数的贡献得单独算，因为它不是一个完整区间
也很简单啊， 求出最后一个小于等于$n$的质数$P_1$和第一个大于$n$的质数$P_2$
计算方法也是一样的啊，只不过乘的个数不一样罢了👉$\frac{n-P_1+1}{P_1\ast P_2}$
我们可以感性猜想两个素数之间按道理是不会差太多的，也就是说应该能放得过我的暴力寻找
证不来那就感性猜想走一波

code

#include <cstdio>
#define ll long long
int T, n;
ll pre, suf;bool check( ll x ) {for( ll i = 2;i * i <= x;i ++ )if( x % i == 0 ) return 0;return 1;
}ll GCD( ll x, ll y ) {if( ! y ) return x;else return GCD( y, x % y );
}ll LCM( ll x, ll y ) {ll d = GCD( x, y );return x / d * y;
}int main() {scanf( "%d", &T );while( T -- ) {scanf( "%d", &n );		pre = n, suf = n + 1;while( ! check( pre ) ) pre --;while( ! check( suf ) ) suf ++;ll x1 = pre - 2, y1 = ( pre << 1 ), x2 = n - pre + 1, y2 = pre * suf;ll lcm = LCM( y1, y2 );ll ansx = lcm / y1 * x1 + lcm / y2 * x2;ll ansy = lcm;ll d = GCD( ansx, ansy );printf( "%lld/%lld\n", ansx / d, ansy / d );}return 0;
}

精灵

Branimirko 是一个对可爱精灵宝贝十分痴迷的玩家。最近，他闲得没事组织了一场捉精 灵的游戏。游戏在一条街道上举行，街道上一侧有一排房子，从左到右房子标号由 1 到 n。 刚开始玩家在 k 号房子前。有 m 个精灵，第 i 只精灵在第 A[i]栋房子前，分值是 B[i]， 以及它在 T[i]秒内（含）存在，之后消失。Branimirko 可以选择移动至相邻的房子，耗时 1 秒。抓住精灵不需要时间，精灵被抓住后消失。时间从第 1 秒开始。Branimirko 能最多获得 多少分值和。

输入格式
输入的第 1 行为三个正整数 n，k，m。 接下来 m 行描述精灵的信息，分别为 A[i]，B[i]，T[i]。

输出格式
输出 Branimirko 能最多获得多少分值和。

样例
样例输入
10 5 4
1 30 4
3 5 7
7 10 12
9 100 23
115
数据范围与提示
20%的数据：𝑚 ≤ 10 40%的数据：𝑚 ≤ 20 对于 100%的数据：𝑘 ≤ 𝑛 ≤ 1000, 𝑚 ≤ 100, 𝐴[𝑖] ≤ 𝑁, 𝐵[𝑖] ≤ 100, 𝑇[𝑖] ≤ 2000，所有数为正整数

solution

这道题好啊，这道题妙啊，这道题顶呱呱啊

首先读题读完就应该有了dp的方向，略微思考那么一丢丢（直接就看得出来）肯定是区间dp没得跑了，接着去看看数据范围，嗯针不戳确定三四维差不多了
这里精灵只有$m$个，地点的范围级别是精灵的十倍，所以我们应该是用精灵进行区间dp
不会有人硬刚n吧，不会吧不会吧

$dp[l][r][t][0/1]$：表示在$t$时刻，已经$\ast$完了$[l,r]$内所有能艹的精灵，此时是在$l(0)/r(1)$位置上的最大收益
然后就可以暴力四个转移方程转移了
{f[l][r][t][0]=max{f[l+1][r][t−(g[l+1].p−g[l].p)][0]+g[l].s}l+1=>lf[l][r][t][0]=max{f[l+1][r][t−(g[r].p−g[l].p)][1]+g[l].s}r=>lf[l][r][t][1]=max{f[l][r−1][t−(g[r].p−g[r−1].p)][1]+g[r].s}r−1=>rf[l][r][t][1]=max{f[l][r−1][t−(g[r].p−g[l].p)][0]+g[r].s}l=>r\left\{ \begin{aligned} f[l][r][t][0] = max\{f[l + 1][r][t - ( g[l + 1].p - g[l].p )][0] + g[l].s\}\ l+1=>l\\ f[l][r][t][0] =max\{f[l + 1][r][t - ( g[r].p - g[l].p )][1] + g[l].s\}\ r=>l\\ f[l][r][t][1]=max\{f[l][r - 1][t - ( g[r].p - g[r - 1].p )][1] + g[r].s\}\ r-1=>r\\ f[l][r][t][1]=max\{f[l][r-1][t-(g[r].p-g[l].p)][0]+g[r].s\}\ l=>r\\ \end{aligned} \right. ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧​f[l][r][t][0]=max{f[l+1][r][t−(g[l+1].p−g[l].p)][0]+g[l].s} l+1=>lf[l][r][t][0]=max{f[l+1][r][t−(g[r].p−g[l].p)][1]+g[l].s} r=>lf[l][r][t][1]=max{f[l][r−1][t−(g[r].p−g[r−1].p)][1]+g[r].s} r−1=>rf[l][r][t][1]=max{f[l][r−1][t−(g[r].p−g[l].p)][0]+g[r].s} l=>r​
一般dp左右都会对其造成影响的dp就可以往区间dp上去思考

code

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define maxt 2005
#define maxm 105
struct node {int p, s, t;
}g[maxm];
int n, k, m, maxT;
int f[maxm][maxm][maxt][2];bool cmp( node x, node y ) {return x.p < y.p;
}int Fabs( int x ) {return ( x < 0 ) ? -x : x;
}int main() {memset( f, -0x3f, sizeof( f ) );scanf( "%d %d %d", &n, &k, &m );for( int i = 1;i <= m;i ++ ) {scanf( "%d %d %d", &g[i].p, &g[i].s, &g[i].t );maxT = max( maxT, g[i].t );}sort( g + 1, g + m + 1, cmp );for( int i = 1;i <= m;i ++ )if( Fabs( g[i].p - k ) + 1 > g[i].t ) continue;else f[i][i][Fabs( g[i].p - k ) + 1][0] = f[i][i][Fabs( g[i].p - k ) + 1][1] = g[i].s;for( int len = 2;len <= m;len ++ ) {for( int l = 1;l + len - 1 <= m;l ++ ) {int r = l + len - 1;for( int t = 1;t <= maxT;t ++ ) {if( t - ( g[l + 1].p - g[l].p ) > 0 )f[l][r][t][0] = max( f[l][r][t][0], f[l + 1][r][t - ( g[l + 1].p - g[l].p )][0] );if( t - ( g[l + 1].p - g[l].p ) > 0 && t <= g[l].t )f[l][r][t][0] = max( f[l][r][t][0], f[l + 1][r][t - ( g[l + 1].p - g[l].p )][0] + g[l].s );if( t - ( g[r].p - g[l].p ) > 0 )f[l][r][t][0] = max( f[l][r][t][0], f[l + 1][r][t - ( g[r].p - g[l].p )][1] );if( t - ( g[r].p - g[l].p ) > 0 && t <= g[l].t )f[l][r][t][0] = max( f[l][r][t][0], f[l + 1][r][t - ( g[r].p - g[l].p )][1] + g[l].s );if( t - ( g[r].p - g[r - 1].p ) > 0 )f[l][r][t][1] = max( f[l][r][t][1], f[l][r - 1][t - ( g[r].p - g[r - 1].p )][1] );if( t - ( g[r].p - g[r - 1].p ) > 0 && t <= g[r].t )f[l][r][t][1] = max( f[l][r][t][1], f[l][r - 1][t - ( g[r].p - g[r - 1].p )][1] + g[r].s );if( t - ( g[r].p - g[l].p ) > 0 )f[l][r][t][1] = max( f[l][r][t][1], f[l][r - 1][t - ( g[r].p - g[l].p )][0] );if( t - ( g[r].p - g[l].p ) > 0 && t <= g[r].t )f[l][r][t][1] = max( f[l][r][t][1], f[l][r - 1][t - ( g[r].p - g[l].p )][0] + g[r].s );}}}int ans = 0;for( int l = 1;l <= m;l ++ )for( int r = l;r <= m;r ++ )for( int t = 1;t <= maxT;t ++ )ans = max( ans, max( f[l][r][t][0], f[l][r][t][1] ) );printf( "%d\n", ans );return 0;
}

农夫约的假期

在某国有一个叫农夫约的人，他养了很多羊，其中有两头名叫 mm 和 hh，他们的歌声 十分好听，被当地人称为“魔音”······ 农夫约也有自己的假期呀！他要去海边度假，然而 mm 和 hh 不能离开他。没办法，他 只好把他们两个带上。 到了海边，农夫约把他的羊放在一个(nn)的矩阵(有 nn 个方格)里。mm 和 hh 十分好 动，他们要走到 m(m<=n*n)个地方，第 i 个地方的坐标为(xi,yi)，每到一个地 方他们会高歌一曲，制造 q[i]点魔音值，因为他们的魔音十分独特，他们的声音只能横着或 竖着传播。每传播一格，魔音值会增加 1。(传播的格子数取最小的)接下来农夫约要住酒店。 为了方便照顾小羊们，他选的酒店的坐标要在矩阵内。但小羊们的魔音让他十分头疼。他想 求出魔音值最小的地方。 他还要享受他的假期，所以他把这个任务交给你了，加油(^_)。

输入格式
第一行输入 n、m 和 z。 接下来 m 行，每行 3 个正整数 x[i],y[i]和 q[i]。

输出格式
第一行一个整数表示魔音值最小是多少。 接下来一行两个正整数 zb1 和 zb2，表示魔音值最小的地方的坐标(如果有多个答案， 输出横坐标最小的情况下，纵坐标最小的)。

样例
输入样例
3 3 1
1 1 1
1 2 1
1 3 1
输出样例
5
1 2
数据范围与提示
10%的数据，n<=10. 30%的数据，n<=1000. 100%的数据，0<n<=100000， 0<m<=100000，0<q[i]<=100.

solution

语文是个好东西，读题读了半个小时硬是没读懂

样例解释你写了跟没写一样，呵呵呵呵

读懂过后就发现比素数还简单
这个饶了™山路十八弯的距离说白了的曼哈顿距离，横坐标差绝对值+纵坐标差绝对值
于是自然而然地
想到了
将$x,y$分开处理，彼此是不影响的
二维就被降成了一维
一个数轴上一堆点，求它们到一个点的距离最小值
就是中位数噻 这还反应不过来？？
题目要求有多个答案，先保证$x$最小，再保证$y$最小
根据计算机除法计算的特别性，管它奇偶，老子直接$>>1$搞定
所以这道题就是两个sort排序取两个中位数$x_{mid},y_{mid}$，然后算$m$个点与该点的曼哈顿距离

code

#include <cstdio>
#include <algorithm>
using namespace std;
#define maxn 100005
struct node {int x, y, q;
}s[maxn];
int n, m, z;bool cmp1( node x, node y ) {return x.x < y.x;
}bool cmp2( node x, node y ) {return x.y < y.y;
}int Fabs( int x ) {return ( x < 0 ) ? -x : x;
}int main() {scanf( "%d %d %d", &n, &m, &z );for( int i = 1;i <= m;i ++ )scanf( "%d %d %d", &s[i].x, &s[i].y, &s[i].q );sort( s + 1, s + m + 1, cmp1 );int ansx = s[( m + 1 ) >> 1].x;sort( s + 1, s + m + 1, cmp2 );int ansy = s[( m + 1 ) >> 1].y;long long ans = 0;for( int i = 1;i <= m;i ++ )ans += Fabs( s[i].x - ansx ) + Fabs( s[i].y - ansy ) + s[i].q;printf( "%lld\n%d %d", ans, ansx, ansy );return 0;
}

观察

solution

infleaking 十分愉快地走在路上，因为经过 10⁹9^9 年后，他得到了一个新技能—— 观察大法。 刚出来的 infleaking 就想要挑战自我。 为什么 infleaking 会这么自信呢？ 因为 infleaking 做到了可以通过观察数据就就可以得出答案。 但是出题人十分不服，想要将 infleaking 的气焰打压下去，于是想到了一道题。 结果被 infleaking 运用他那强大的观察能力看完数据后给出了答案。 怎么能够让 infleaking 继续下去呢，出题人于是就将数据重出并且加密了。 没有能直接观察数据的 infleaking 十分不服气，想要解决这道题，但是苦于不能直接使 用他的新技能，所以想要请聪明的你帮 infleaking 解决这个问题。 出题人给出一颗以 1 为根的树，一开始每个节点都是一颗棋子，一面白一面黑，白色的 面朝上接下来就 q 次操作，操作分两种 0 操作 将一个颗棋子翻转 1 操作 询问一颗棋子与所有面朝上为黑色的棋子 lca 最深的那个的编号

输入格式
第 1 行，两个正整数 n，q 第 2 行，一共 n-1 个正整数，第 i 个正整数表示 i+1 号结点的父亲 第 3~q+3 每行两个整数 x ，第|x|个为被操作的棋子，x>0 操作为 0 否则为 1

输出格式
对于每个 op 为 1 的操作输出对应的编号，若场上没有黑棋子输出 0

样例
样例输入
10 10
6 2 7 9 1 10 5 4 3
-2
1
3
3
-5
8
1
4
-1
-5
样例输出
0
1
1
5
数据范围与提示
100%的数据，n，q<=800000

solution

有一个结论
好家伙这场是结论专场了吧
一个点肯定跟dfn序离自己最近的两个点（前后各一个）lca最大
这个结论errrr——，怎么证明呢？？感性理解吧，毕竟虚树就是在这个结论基础上做的

于是就可以用一个数据结构维护所有黑点的$dfn$序
这里我们选择既好写又可爱的 set
小儿子考场用的set，但他不会，半天编译过不了，于是他生气了，敲了个treap

但是考后OJ上，被卡了？？？T了——啊这，这波我没有想到
于是乎手动O(2)，lca用树链剖分去搞，再加上多次提交，最后终于卡过去了一次

code

#pragma GCC optimize(2)
#include <set>
#include <cstdio>
#include <vector>
using namespace std;
#define maxn 800005
set < int > st;
set < int > :: iterator it;
vector < int > G[maxn];
int n, Q, cnt;
int dfn[maxn], dep[maxn], rnk[maxn], siz[maxn], son[maxn], top[maxn], f[maxn];void dfs1( int u ) {dfn[u] = ++ cnt, rnk[cnt] = u, dep[u] = dep[f[u]] + 1, siz[u] = 1;for( int i = 0;i < G[u].size();i ++ ) {int v = G[u][i];f[v] = u;dfs1( v );siz[u] += siz[v];if( ! son[u] || siz[v] > siz[son[u]] )son[u] = v;}
}void dfs2( int u, int t ) {top[u] = t;if( ! son[u] ) return;dfs2( son[u], t );for( int i = 0;i < G[u].size();i ++ ) {int v = G[u][i];if( v == son[u] ) continue;else dfs2( v, v );}
}int lca( int u, int v ) {while( top[u] ^ top[v] ) {if( dep[top[u]] > dep[top[v]] )u = f[top[u]];elsev = f[top[v]];}return ( dep[u] < dep[v] ) ? u : v;
}int main() {scanf( "%d %d", &n, &Q );for( int i = 2, fa;i <= n;i ++ ) {scanf( "%d", &fa );G[fa].push_back( i );}dfs1( 1 );dfs2( 1, 1 );while( Q -- ) {int x;scanf( "%d", &x );if( x < 0 ) {x = -x;if( st.empty() ) printf( "0\n" );else {it = st.upper_bound( dfn[x] );int lca1 = 0, lca2 = 0;if( it != st.end() ) lca2 = lca( x, rnk[*it] );if( it != st.begin() ) it --, lca1 = lca( x, rnk[*it] );if( dep[lca1] > dep[lca2] ) printf( "%d\n", lca1 );else printf( "%d\n", lca2 );}}else {it = st.find( dfn[x] );if( it == st.end() ) st.insert( dfn[x] );else st.erase( it ); }}return 0;
}