解析

在斜优的时候，有时我们会发现我们插入的点的横坐标并不单调
这个时候我们就无法利用单调队列维护凸包了
这时，我们就要请出今天的主角：splay

插点

splay斜优最容易错的一个地方
我们维护一个以结点横坐标作为关键值的splay
结点记录第信息有：左右儿子、父亲、xy坐标、分别与左右两边第一个结点的斜率
注意这个第一个结点不一定是左右儿子！
特别的，没有儿子时赋值成正（右）负（左）无穷

step1

首先，让我们把结点按照splay的常规操作塞进去

if(!rt){rt=New(x,y,id,0);lk[rt]=-2e18;rk[rt]=2e18;return;}int now=rt;while(1){if(tr[now][x>dx[now]]) now=tr[now][x>dx[now]];else{tr[now][x>dx[now]]=New(x,y,id,now);splay(tot);break;}}

step2

但是这样，可能凸包的性质会被打破
我们需要继续维护凸包的性质
首先，这个结点可能会是两边的点变成需要去掉的上凸点
下面以左侧为例

加入一个x点时：
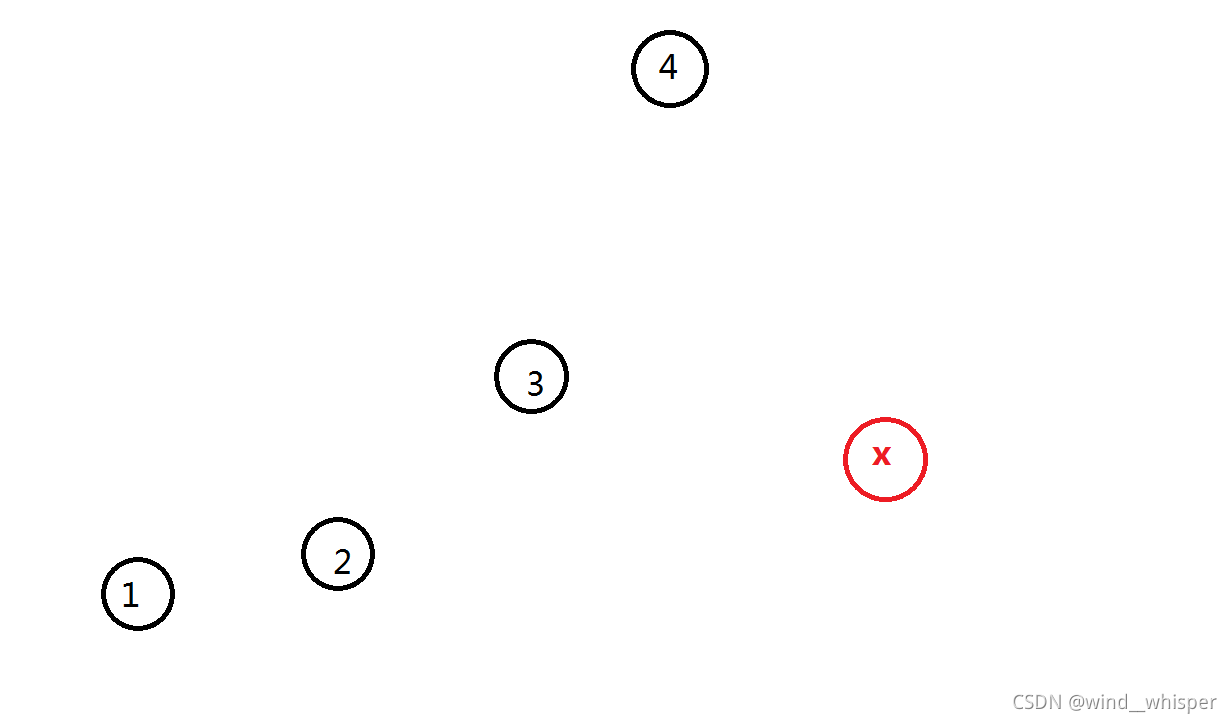
请添加图片描述
显然，3点和4点应该舍去
在原本的点集满足凸包性质的前提下
我们其实只需要找到左边第一个满足 $lk_i<slope(i,x)$ 的点 （在本图中就是2）
我们可以在splay上通过类似二分的方法来实现这个操作

inline int pre(){int now=tr[rt][0],res=0;while(now){if(lk[now]<slope(now,rt)+eps){res=now;now=tr[now][1];}else now=tr[now][0];}return res;
}

找到这个pre之后，把pre和当前点之间的点全部删去即可

if(tr[now][0]){int o=pre();//printf("?:\n");splay(o,now);tr[o][1]=0;lk[now]=rk[o]=slope(o,now);}

记得更新斜率！！！

step3

考虑到当前点本身可能就是上凸点
我们特判一下如果是直接把它删掉即可
特判的依据就是 $lk_x>rk_x$
注意这个特判必须在step2之后！！
为什么？因为x的lk和rk都是在step2求的…

if(lk[now]>rk[now]+eps){int ls=tr[now][0],rs=tr[now][1];f[ls]=0;rt=ls;tr[ls][1]=rs;f[rs]=ls;lk[rs]=rk[ls]=slope(ls,rs);}

查询

对于一个斜率k
找到 $lki≤k≤rkilk_i \leq k \leq rk_i$ 的位置即可
相对比较简单

if(lk[now]>rk[now]+eps){int ls=tr[now][0],rs=tr[now][1];f[ls]=0;rt=ls;tr[ls][1]=rs;f[rs]=ls;lk[rs]=rk[ls]=slope(ls,rs);}

update

本题中的横坐标两两不同，但有些题并非如此，需要特判横坐标相同的情况！
具体而言，只需要在插点的地方这么写：

	int x;//这里维护的上凸包if(!now) rt=New(xx,yy,0),x=rt;else{while(1){if(abs(dx[now]-xx)<eps){if(dy[now]<yy) return;else{dy[now]=yy;splay(now);x=now;break;}}if(tr[now][xx>dx[now]]) now=tr[now][xx>dx[now]];else{tr[now][xx>dx[now]]=New(xx,yy,now);splay(tot);x=tot;break;}}}.......

代码

主函数就变得非常easy！

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define il inline
#define debug(a) fprintf(stderr,a)
const int N=5e5+1000;
const int M=3e6+100;
const int mod=998244353;
const double eps=1e-10;
inline ll read(){ll x=0,f=1;char c=getchar();while(!isdigit(c)){if(c=='-') f=-1;c=getchar();}while(isdigit(c)){x=x*10+c-'0';c=getchar();}return x*f;
}
int n,m;
int tr[N][2],f[N],idx[N],rt,tot;
double lk[N],rk[N],dx[N],dy[N];
inline int New(double x,double y,int id,int fa){++tot;tr[tot][0]=tr[tot][1]=0;f[tot]=fa;dx[tot]=x;dy[tot]=y;idx[tot]=id;return tot;
}
inline bool which(int x){return tr[f[x]][1]==x;}
inline void rotate(int x){int fa=f[x],gfa=f[fa];int d=which(x),son=tr[x][d^1];f[x]=gfa;if(gfa) tr[gfa][which(fa)]=x;f[fa]=x;tr[x][d^1]=fa;if(son) f[son]=fa;tr[fa][d]=son;return;
}
inline void splay(int x,int goal=0){//printf("x=%d goal=%d fa=%d\n",x,goal,f[x]);for(int fa;(fa=f[x])!=goal;rotate(x)){if(f[fa]!=goal) which(fa)==which(x)?rotate(fa):rotate(x);}if(!goal) rt=x;return;
}
#define slope(u,v) ((dy[v]-dy[u])/(dx[v]-dx[u]))
inline int pre(){int now=tr[rt][0],res=0;while(now){if(lk[now]<slope(now,rt)+eps){res=now;now=tr[now][1];}else now=tr[now][0];}return res;
}
inline int nxt(){int now=tr[rt][1],res=0;while(now){if(rk[now]+eps>slope(rt,now)){res=now;now=tr[now][0];}else now=tr[now][1];}return res;
}
inline void ins(double x,double y,int id){if(!rt){rt=New(x,y,id,0);lk[rt]=-2e18;rk[rt]=2e18;return;}int now=rt;while(1){if(tr[now][x>dx[now]]) now=tr[now][x>dx[now]];else{tr[now][x>dx[now]]=New(x,y,id,now);splay(tot);break;}}//for(int i=1;i<=tot;i++) printf("i=%d ls=%d rs=%d (%.3lf %.3lf)\n",i,tr[i][0],tr[i][1],dx[i],dy[i]);now=rt;if(tr[now][0]){int o=pre();//printf("?:\n");splay(o,now);tr[o][1]=0;lk[now]=rk[o]=slope(o,now);}else lk[now]=-2e18;if(tr[now][1]){int o=nxt();splay(o,now);tr[o][0]=0;rk[now]=lk[o]=slope(o,now);}else rk[now]=2e18;if(lk[now]>rk[now]+eps){int ls=tr[now][0],rs=tr[now][1];f[ls]=0;rt=ls;tr[ls][1]=rs;f[rs]=ls;lk[rs]=rk[ls]=slope(ls,rs);}return;
}
int query(double k){int now=rt;while(1){if(!now) return 0;//printf("now=%d lk=%.3lf rk=%.3lf (%.3lf %.3lf)\n",now,lk[now],rk[now],dx[now],dy[now]);if(lk[now]-eps<=k&&k<=rk[now]+eps) return idx[now];else if(lk[now]+eps>k) now=tr[now][0];else now=tr[now][1];}
}
double ans=2e18;
int v[N];
ll x[N];
double dp[N],r[N];
#define X(o) (-1.0/(2.0*sqrt(r[o])))
#define Y(o) (dp[o]-1.0*x[o]/(2*sqrt(r[o])))
int main() {
#ifndef ONLINE_JUDGEfreopen("a.in","r",stdin);freopen("a.out","w",stdout);
#endifn=read();m=read();for(int i=1;i<=n;i++){x[i]=read();r[i]=read();v[i]=read();}dp[1]=v[1];ins(X(1),Y(1),1);//printf("  i=%d dp=%.3lf (%.3lf,%.3lf)\n\n",1,dp[1],X(1),Y(1));for(int i=2;i<=n;i++){//printf("i=%d\n",i);int j=query(x[i]);//printf("  ok\n");dp[i]=dp[j]+1.0*(x[i]-x[j])/(2*sqrt(r[j]))+v[i];//printf("  j=%d i=%d dp=%.3lf (%.3lf,%.3lf)\n\n",j,i,dp[i],X(i),Y(i));ins(X(i),Y(i),i);if(x[i]+r[i]>=m) ans=min(ans,dp[i]);}//printf("ceck:%3lf\n",slope(1,2));printf("%.3lf\n",ans);return 0;
}
/*
3 1
3 1 33 2
1 1 2
3 1 3
*/