文章目录
- 一:CF1463F
- 二:CF1152F2
- 三:CF1342F
一:CF1463F
Max Correct Set
有一个结论:以x+yx+yx+y为周期排列填充一定是不劣于最后的答案的
令p=x+y,r=n%pp=x+y,r=n\%pp=x+y,r=n%p
⌊np⌋\lfloor\frac{n}{p}\rfloor⌊pn⌋出现次数为ttt次,则rrr的出现次数为t+1t+1t+1,预处理一下即可
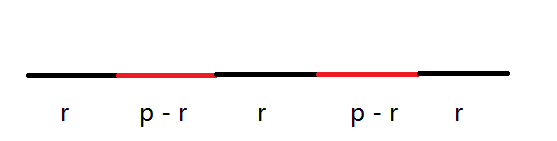
设dpi,sdp_{i,s}dpi,s表示一段ppp中的某个点iii为断点,最后max(x,y)max(x,y)max(x,y)位的状态为jjj的答案数
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
int n, x, y;
int dp[2][1 << 22], val[50];int main() {scanf( "%d %d %d", &n, &x, &y );int p = x + y, r = n % p;for( int i = 0;i < p;i ++ )val[i] = n / p + ( i < r );int S = 1 << max( x, y );memset( dp, -1, sizeof( dp ) );dp[1][0] = 0;for( int i = 0;i < p;i ++ ) {int now = i & 1;memset( dp[now], -1, sizeof( dp[now] ) );for( int j = 0;j < S;j ++ )if( ~ dp[now ^ 1][j] ) {dp[now][j << 1 & S - 1] = max( dp[now][j << 1 & S - 1], dp[now ^ 1][j] );if( ! ( 1 << x - 1 & j ) && ! ( 1 << y - 1 & j ) )dp[now][j << 1 & S - 1 | 1] = max( dp[now][j << 1 & S - 1 | 1], dp[now ^ 1][j] + val[i] );}}int ans = 0;for( int i = 0;i < S;i ++ )ans = max( ans, dp[( p - 1 ) & 1][i] );printf( "%d\n", ans );return 0;
}
二:CF1152F2
Neko Rules the Catniverse (Large Version)
简单版:
设dpi,j,sdp_{i,j,s}dpi,j,s:表示前iii个数,从中选了jjj个,离iii最近的mmm个元素是否选择的状态sss
考虑转移到i+1i+1i+1
iii不选,直接转移到dpi+1,j,s>>1dp_{i+1,j,s>>1}dpi+1,j,s>>1,(舍去距离iii为mmm的元素,该元素距离i+1i+1i+1变成了m+1m+1m+1,丢掉
iii选,那么这个元素可以放在最后距离≤m\le m≤m个元素中选了的元素后面,或者放在第一个(目前iii是最大的,一定可以放在最前面
#include <cstdio>
#define int long long
#define mod 1000000007
int n, k, m;
int dp[100005][14][1 << 4];signed main() {scanf( "%lld %lld %lld", &n, &k, &m );dp[0][0][0] = 1;for( int i = 0;i < n;i ++ )for( int j = 0;j <= k;j ++ )for( int s = 0;s < ( 1 << m );s ++ ) {dp[i + 1][j][s >> 1] = ( dp[i + 1][j][s >> 1] + dp[i][j][s] ) % mod;dp[i + 1][j + 1][s >> 1 | 1 << m - 1] = ( dp[i + 1][j + 1][s >> 1 | 1 << m - 1] + dp[i][j][s] * ( __builtin_popcount( s ) + 1 ) % mod ) % mod;}int ans = 0;for( int i = 0;i < ( 1 << m );i ++ )ans = ( ans + dp[n][k][i] ) % mod;printf( "%lld\n", ans );return 0;
}
加强版是建立在发现简单版的第二维和第三维大小一共在210210210左右
是可以用矩阵快速幂优化的,把第二维和第三维压在一起重新编号代替
#include <cstdio>
#include <cstring>
#define int long long
#define mod 1000000007
int n, k, m, cnt;
int id[15][20];struct matrix {int c[210][210];//2^4*13=208matrix() {memset( c, 0, sizeof( c ) );}matrix operator * ( matrix &v ) {matrix ans;for( int i = 1;i <= cnt;i ++ )for( int j = 1;j <= cnt;j ++ )for( int k = 1;k <= cnt;k ++ )ans[i][j] = ( ans[i][j] + c[i][k] * v[k][j] % mod ) % mod;return ans;}int *operator [] ( int x ) { return c[x]; }
}g, f;signed main() {scanf( "%lld %lld %lld", &n, &k, &m );for( int i = 0;i <= k;i ++ )for( int j = 0;j < ( 1 << m );j ++ )id[i][j] = ++ cnt;for( int i = 0;i <= k;i ++ )for( int s = 0;s < ( 1 << m );s ++ ) {
// int t = s << 1 & ( ( 1 << m ) - 1 );
// ( g[id[i][s]][id[i][t]] += 1 ) %= mod;
// if( i < k ) ( g[id[i][s]][id[i + 1][t | 1] += __builtin_popcount( s ) + 1 ) %= mod;
//两种写法均是正确的( g[id[i][s]][id[i][s >> 1]] += 1 ) %= mod;if( i < k ) ( g[id[i][s]][id[i + 1][s >> 1 | 1 << m - 1]] += __builtin_popcount( s ) + 1 ) %= mod;}f[1][1] = 1;while( n ) {if( n & 1 ) f = f * g;g = g * g;n >>= 1;}int ret = 0;for( int i = 0;i < ( 1 << m );i ++ )ret = ( ret + f[1][id[k][i]] ) % mod;printf( "%lld\n", ret );return 0;
}
三:CF1342F
Make It Ascending
设dpi,j,sdp_{i,j,s}dpi,j,s:表示划分了iii个集合,最后一个集合的合并点在jjj,最后一个集合选择的点状态为sss
小贪心:一个集合的合并点肯定越靠前越好,集合的和在大于上一个集合的条件下越小越好;这样都是为了增大后面再划分一个集合的概率
预处理集合为sss的aaa值和,然后直接转移就没了o(=·ω·=)m
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
#define INF 0x7f7f7f7f
int T, n;
int a[16], sum[1 << 15], id[16];
pair < int, int > pre[16][16][1 << 15];
int f[16][16][1 << 15];void opt( int x ) {for( int i = x;i < n;i ++) id[i] --;
}void print( int i, int pos, int s ) {if( ! s ) return;int lst = pre[i][pos][s].first, t = lst ^ s;for( int k = 0;k < n;k ++ )if( k != ( pos - 1 ) && ( 1 << k & t ) ) {printf( "%d %d\n", id[k], id[pos - 1] );opt( k );}print( i - 1, pre[i][pos][s].second, lst );
}void solve() {scanf( "%d", &n );for( int i = 0;i < n;i ++ )scanf( "%d", &a[i] );int S = 1 << n;for( int i = 1;i < S;i ++ )sum[i] = a[__builtin_ctz( i )] + sum[i & ( i - 1 )];for( int i = 0;i <= n;i ++ )for( int j = 0;j <= n;j ++ )memset( f[i][j], 0x7f, sizeof( int ) * S );f[0][0][0] = 0;for( int i = 0;i < n;i ++ )for( int s = 0;s < S;s ++ )for( int j = 0;j < n;j ++ ) {if( f[i][j][s] == INF ) continue;int t = ( S - 1 ) ^ s;for( int k = t;k;k = ( k - 1 ) & t ) {if( sum[k] <= f[i][j][s] || ! ( k >> j ) ) continue;int pos = j + __builtin_ctz( k >> j ) + 1;if( f[i + 1][pos][s | k] > sum[k] ) {f[i + 1][pos][s | k] = sum[k];pre[i + 1][pos][s | k] = make_pair( s, j );}}}for( int i = 0;i < n;i ++ ) id[i] = i + 1;for( int i = n;i;i -- )for( int j = 1;j <= n;j ++ )if( f[i][j][S - 1] != INF ) {printf( "%d\n", n - i );print( i, j, S - 1 );return;}
}int main() {scanf( "%d", &T );while( T -- ) solve();return 0;
}



![P3642 [APIO2016]烟火表演(左偏树、函数)](http://pic.xiahunao.cn/P3642 [APIO2016]烟火表演(左偏树、函数))
)




)




)

)

GPIO 的使用)
