背景

系列目录：【NET CORE微服务一条龙应用】开始篇与目录

在分布式或者微服务系统里，通过配置文件来管理配置内容，是一件比较令人痛苦的事情，再谨慎也有湿鞋的时候，这就是在项目架构发展的过程中，配置中心存在的意义。

其实配置中心的组件已经有非常出名的案例，比如携程的阿波罗配置中心（https://github.com/ctripcorp/apollo）

为什么又造轮子，因为不想发布项目的时候到处切管理平台。

基本要求

作为一个通用的配置组件，需要支持如下功能：

1、客户端定时刷新获信最新配置信息并进行热更新

2、配置有更新服务端主动推送重载或更新命令至客户端进行配置获取

所以涉及相对应组件如下：

1、支持广播的消息通知组件，目前使用redis(StackExchange.Redis)、Zookeeper(Rabbit.Zookeeper)实现客户端全局监听服务，服务端可以推送不同组建不同的命令

2、支持定时获取最新配置，目前使用HostedService实现全局统一启动，客户端实现全局启动接口，接口使用Timer进行定时获取配置

3、支持net core原生IConfiguration接口获取配置中心数据

 服务端设计

 

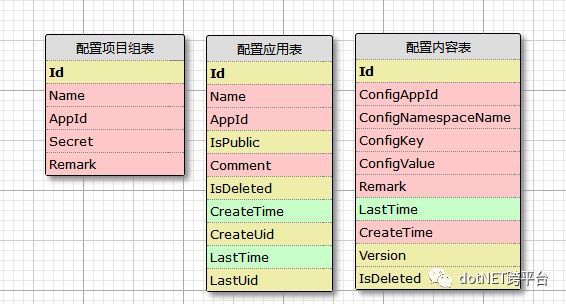
管理服务端主要实现：

1、三表增删改查

2、配置内容表，每次新增或者修改，当前配置信息版本号为，所以配置最大版本号然后加一

3、应用表列表增加主动通知功能

配置查询服务端

主要提供配置信息的查询接口

1、接口入参如下

2、查询逻辑

   2.1 入参基本验证

   2.2 AppId 密钥进行签名验证

   2.3 请求配置环境定位

   2.4 查询当前请求应用和共有配置应用

   2.5 查询大于当前查询版本号的配置信息并返回

配置中心客户端

客户端主要实现原理和功能

1、配置信息请求，当前Http请求，需根据配置信息组合请求url，然后请求获取配置，每次请求带上当前配置最大版本号(在以后请求时只获取有更新的配置）

2、配置信息本地存储（容灾），第一次获取成功后，把配置信息进行版本文件存储，以后的请求中当有配置更新时再进行文件存储。

3、当配置请求失败时进行本地文件配置信息的还原应用。

4、配置定时获取

5、客户端接收更新或者重载命令

6、原生IConfiguration配置查询支持

部分功能介绍

客户端参数

原生IConfiguration配置查询

查看AddJsonFile源码，可以发现实现自定义配置源，需要集成和实现ConfigurationProvider和IConfigurationSource两个方法

代码如下

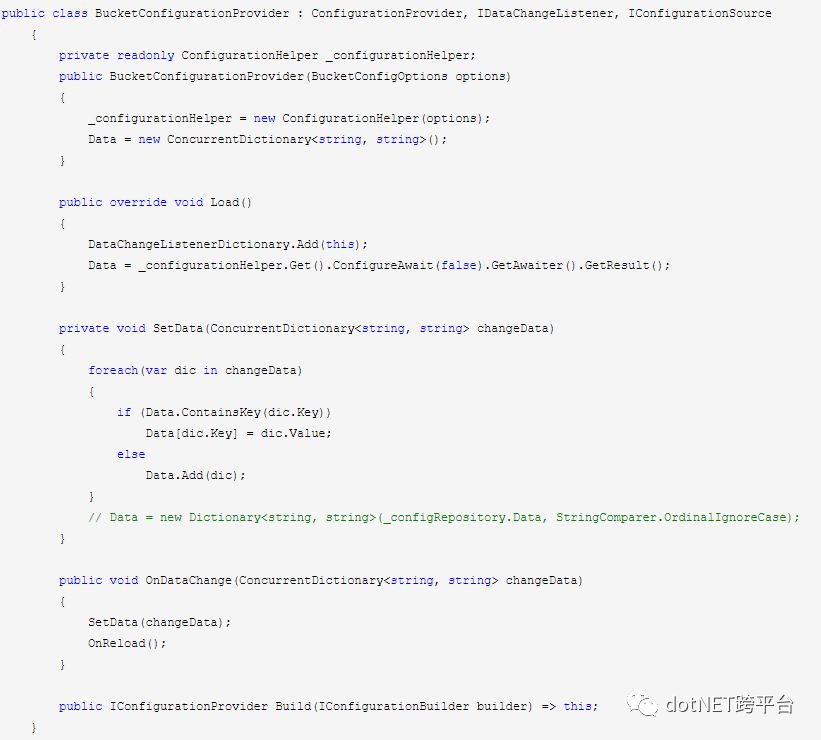
当有配置更新时，我们需要更新到ConfigurationProvider的Data中，所以我们需要实现自定义接口IDataChangeListener的OnDataChange方法，当客户端请求发现有配置更新时，会调用接口的OnDataChange把最新的配置信息传递进来。

启用原生IConfiguration方法如下：

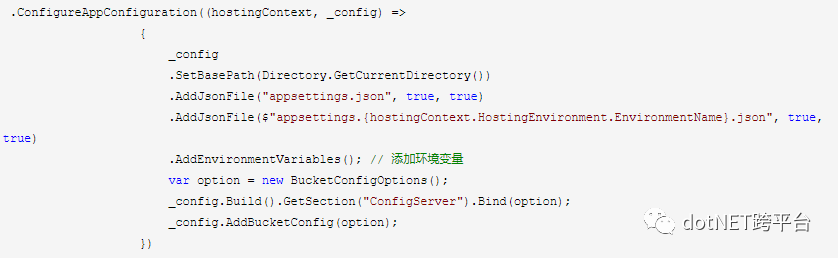
定时配置获取

常规做法是写一个hostedservice的方法，然后写一个timer去定时获取，由于其他的组件可能都需要有定时的情况，我们统一处理了一下定时的任务，每个组件实现IExecutionService接口，然后组件会在启动的时候循环调用IExecutionService的StartAsync的方法，组件包Bucket.Config.HostedService，原理比较简单，使用代码如下：

组件命令监听

和上面原则一样，也进行了统一的封装，目前监听主要实现了redis和zookeeper，下面举例redis

组件监听需实现接口

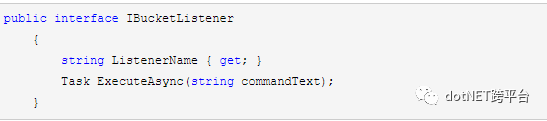
命令序列化实体

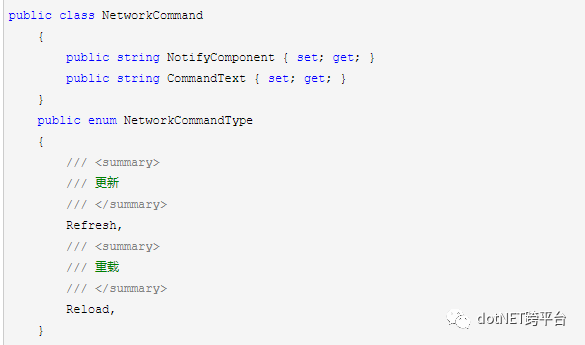
在hostedservice启动时实现

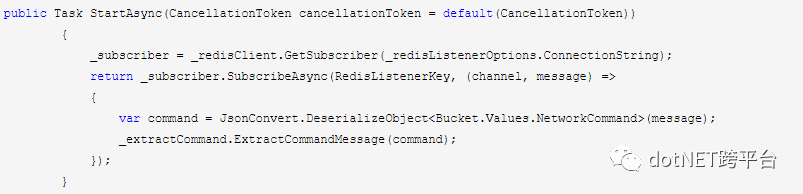
在接口IExtractCommand里会根据各个监听组件的ListenerName进行对应的调用

使用方法如下：

所以对应组件实现的命令监听只要关心自身逻辑即可吗，代码如下

配置中心使用配置如下

Appsettings.json相关配置信息转移至配置中心

由于配置中心客户端实现了原生的IConfiguration，所以appsetting的相关配置我们完全可以移至配置中心中，由于appsetting使用的是json，所以在配置中心服务端配置信息的Key需要转换，举例：

在配置中心key如下：

BucketListener:Redis:ConnectionString

BucketListener:Redis:ListenerKey

......

数组使用如下：

DbConfig:0:Name

DbConfig:0:DbType

DbConfig:1:Name

DbConfig:1:DbType

总结

个人写作水平有限，涉及的东西也很多，篇幅有限所以只做了大体介绍，忘谅解

本章涉及源码
https://github.com/q315523275/FamilyBucket/tree/master/src/Config 客户端组件

https://github.com/q315523275/FamilyBucket/tree/master/%E5%9F%BA%E7%A1%80%E6%9C%8D%E5%8A%A1%E9%A1%B9%E7%9B%AE/Pinzhi.ConfigServer 配置查询服务端

https://github.com/q315523275/FamilyBucket/tree/master/%E5%9F%BA%E7%A1%80%E6%9C%8D%E5%8A%A1%E9%A1%B9%E7%9B%AE/Pinzhi.Platform 综合管理服务接口

相关文章：

• 【NET CORE微服务一条龙应用】第一章 网关使用与配置
  

原文地址：https://www.cnblogs.com/tianxiangzhe/p/10342428.html

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com