C - Rencontre Gym - 102798C
参考题解：
参考一
参考二

题意：

有一棵树，树上的点分为三种，（一个点可以为多种），现在分别在三种点中随机选一点a，b，c，然后找到一个合适的v，使得f=min(dis(a,v)+dis(b,v)+dis(c,v))
求出f的期望

题解：

f = min(dis(a,v)+dis(b,v)+dis(c,v)) = min{1/2( dis(a,b)+ dis(b,c) +dis(a,c) )}
E(f) = 1/2( E(dis(a,b))+E(dis(a,c))+E(dis(b,c)) )
这样a，b，c就是独立的三组，我们要求任意两组内所有点的距离的期望，咋求？

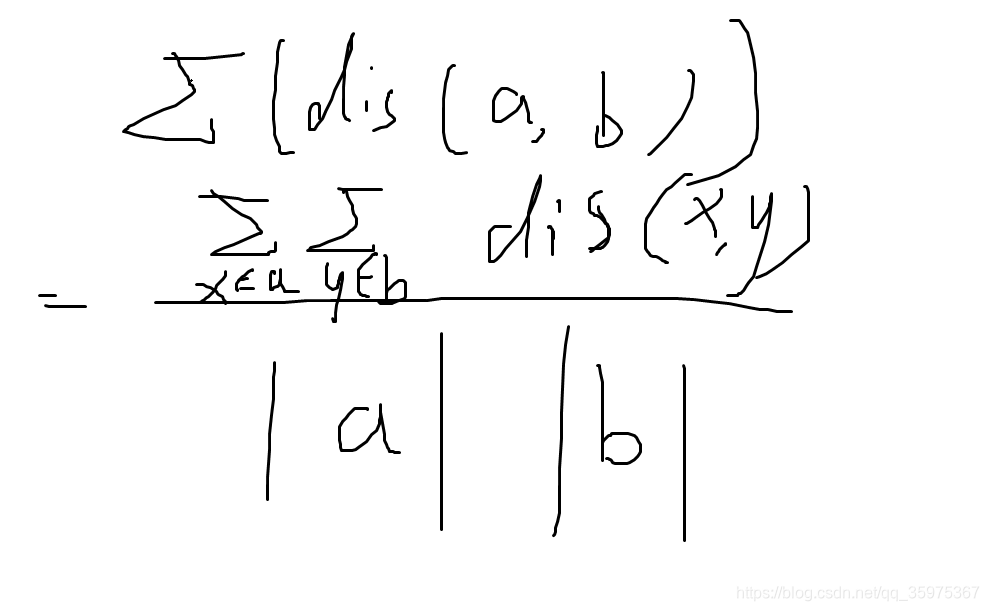
|a|表示集合a内的元素数量
现在问题就是如何快速求任意两点距离和
这个我们可以用换根法来求
对于边(u,v)，其对答案的贡献就是siz[v] * (n-siz[v]) * w
siz[v]表示v的子树中节点数量
n-siz[v]表示非v的子树的节点数量
这两部分中点都可以相互连接
代码中siz[v][1]：表示在v的子树中属于块1的点的数量

代码：

#include <bits/stdc++.h> 
using namespace std;typedef long long ll;
const int N = 1e6 + 10;struct Edge {int v;ll w;
};vector<Edge> g[N];
ll cnt[4], siz[N][4];
double ans;void dfs1(int u, int fa) {for(auto e : g[u]) {int v = e.v;if(v == fa) continue;dfs1(v, u);for(int i = 1;i <= 3; i++) {siz[u][i] += siz[v][i];}}
}void dfs2(int u, int fa) {for(auto e : g[u]) {int v = e.v;if(v == fa) continue;dfs2(v, u);for(int i = 1;i <= 3; i++) {for(int j = 1;j <= 3; j++) {//枚举任意两个块 if(i == j) continue;ans += 1.0 * ((siz[1][i] - siz[v][i]) * siz[v][j] * 1.0 * e.w / (cnt[i] * cnt[j]) / 2.0);/*(siz[1][i] - siz[v][i])表示在子树v之外的属于块i的点的数量siz[v][j]表示在子树v之内的属于块j的点的数量 */ }}}
}void solve() {int n; cin >> n;for(int i = 1;i < n; i++) {int u, v; ll w; cin >> u >> v >> w;g[u].push_back(Edge{v, w});g[v].push_back(Edge{u, w});}for(int i = 1;i <= 3; i++) {cin >> cnt[i];for(int j = 1;j <= cnt[i]; j++) {int x;cin >> x;siz[x][i]++;}}dfs1(1, -1);dfs2(1, -1);printf("%.12f\n",ans);
}int main() {solve();return 0;
}