P3959 [NOIP2017 提高组] 宝藏

题意:

额题意不好说，就是n个点m个边，选定一个点为根节点，构造一个最小生成树，边的权值为该该边起点到根节点之间的点的数量K（不含根节点） * 道路长度
1<=n<=12
0<=m<=1e3
v<=5e5

题解:

参考题解
这数据范围？暴力暴力暴力
不，我们用状压dp来做
我们设dp[i][j]表示用到第i个元素，当前连接状态为j的花费的最小值
这个式子没办法直接转移，因为每个边的花费是不一样的，即k是不一样的，我们可以重新设计一个状态，我们将k值理解为距离初始化点的层数，如图

被涂蓝色的就是根节点，k就是划分的层数
这样我们设dp[i][j]表示到第i层，总共取了的点的状态为j
转移为：
dp[i][j] = min(dp[i-1][k]+trans[k][j] * (i-1))
trans[k][j] * (i-1)就是题目说的距离 * K(题目中说的k)
k是j的子集，即有可能转移到j的状态
trans[k][j]表示从状态k转移到状态j的最小花费路径
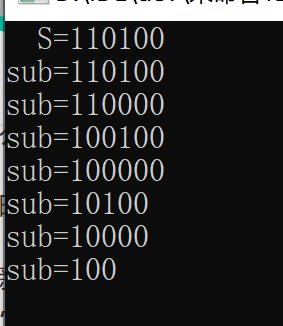
这个子集意思就是：sub就是S的子集
这个子集怎么求？？
直接求2^n必然不行，会T，有小技巧
由公式：

for (int sub = S; sub; sub = (sub - 1) & S) {// sub 为 S 的子集
}

证明过程

最终答案就是：min(dp[i][2ⁿ-1])
初始化：dp[1][2^(i-1)] = 0 (i∈[1,n])
我感觉代码很妙，思路也很妙，让我想是真写不出来
我详细说trans如何求：
现在i是当前状态，j是i的子状态，我们现在要状态转移从j–>i
temp=i ^ j,即要转移的点(因为 ^ 为不同为1)
然后我们开始枚举temp中存在的点k(从高位往低位)，然后求从k到j的最短距离tmin，把tmin加入到trans[j][i]中

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
long long read()
{long long x=0,f=1; char c=getchar();while(!isdigit(c)){if(c=='-') f=-1;c=getchar();}while(isdigit(c)){x=x*10+c-'0';c=getchar();}return x*f;
}
const int N=12+2;
const int M=1<<N;
int n,m,dis[N][N],trans[M][M],POW[N];
long long f[N][M];
int main()
{n=read(),m=read();memset(dis,0x3f,sizeof dis);for(int i=1;i<=m;i++){int s=read(),t=read(),v=read();if(dis[s][t]>v)dis[s][t]=dis[t][s]=v;}for(int i=0;i<(1<<n);i++)for(int j=i;j!=0;j=(j-1)&i){bool OK=true;int temp=i^j;//状态i与状态j的不同之处，状态转移为j->i for(int k=n-1;k>=0;k--){if((temp>>k)&1)//说明点k是转移中增加的点，即 j没有，i有 {int tmin=0x3f3f3f3f;for(int L=1;L<=n;L++)if(1&(j>>(L-1)))//如果状态j包含此点 ,求出L到k+1的最短距离//if(((1<<(L-1))&j)==(1<<(L-1))) tmin=min(tmin,dis[L][k+1]);if(tmin==0x3f3f3f3f)//如果此路无法走通 {OK=false;break;}trans[j][i]+=tmin;/*相当于把j到i这段路拆分成了好几份 */ temp-=(1<<k);}}if(OK==false)trans[j][i]=0x3f3f3f3f;}memset(f,0x3f,sizeof f);for(int i=1;i<=n;i++)f[1][(1<<(i-1))]=0;for(int i=2;i<=n;i++)for(int j=0;j<(1<<n);j++)for(int k=j;k!=0;k=(k-1)&j)//k为j的子状态，也就是k是j的子集 if(trans[k][j]!=0x3f3f3f3f)//说明可以从状态k到j f[i][j]=min(f[i][j],f[i-1][k]+(i-1)*trans[k][j]);long long ans=0x3f3f3f3f3f3f3f3fll;for(int i=1;i<=n;i++)ans=min(ans,f[i][(1<<n)-1]);printf("%lld",ans);return 0;
}