α角 与 β角
支持 现实生活 的 计算机系统,总有着两大偏差,第一个是 现实生活 与 计算机系统 的α角,另外一个是计算机系统的 逻辑设计 与 物理设计 的β角。举个栗子:
α角:假设某个公司的商业流程,我们在做计算机自动化的时候,会发生某种程度的改变。可能是用了新计算机系统,需要调整商业流程;也可能是某些商业流程,由于种种原因,没有被计算机系统实现支持。。。
β角:这个比较常见,例如某个类本身是没有什么ID之类的属性,而由于我们选择了某个数据库产品来做持久化,而数据表的主键用了 某某ID 这样的字段,于是引致我们的 类 里面也可能会包含了 ID 这样的属性;或者由于需要用 SQL Server 的 数据复制 功能,从而使到我们的类加入了各种TimeStamp字段
Entity Split
今天我们讨论的Entity Split,就是属于上述的β角。有时候,由于某些原因(例如 纵向切割 数据表),某个 类 ,它被保存到超过一个的数据表中。例如,我们可能有一个 Customer 类,由于它的属性比较多,于是为了提供系统性能,我们把最常用的属性归纳到 Customers 数据表,而把那些比较少用到的属性归纳到 CustomerOtherInfo 数据表,等等。
在用EF Core的时候,我们会在DbContext.OnModelCreating方法里面用modelBuilder.Entity<MyEntity>().ToTable("Tablename");的做法来指定 BusinessEntity 与 数据表 的映射关系,但是这个只能是Entity级别的,而没有能去到 属性 级别啊 。如何才能做得到指定 “某Entity的某些属性,映射到数据表A;而某些其他属性,映射到数据表B”,这样的效果呢?
(本篇的程序,可以在 https://github.com/kentliu2007/EFCoreDemo/tree/master/EntitySplit 上下载,我用的是 VS2017。建议可以下载之后,对照着程序来阅读本篇)
数据表
先来看看数据表是怎样的:
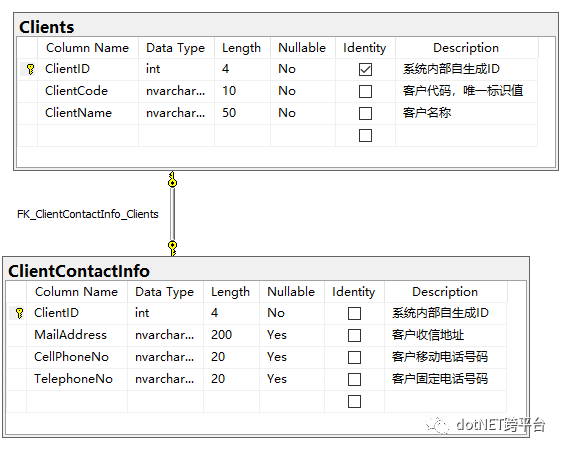
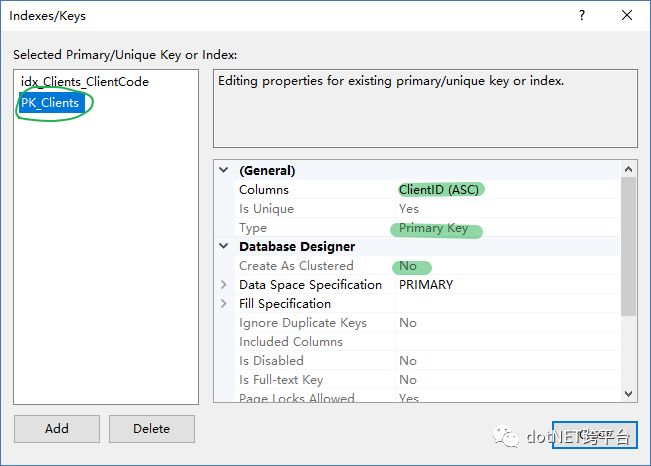
Clients 表的索引
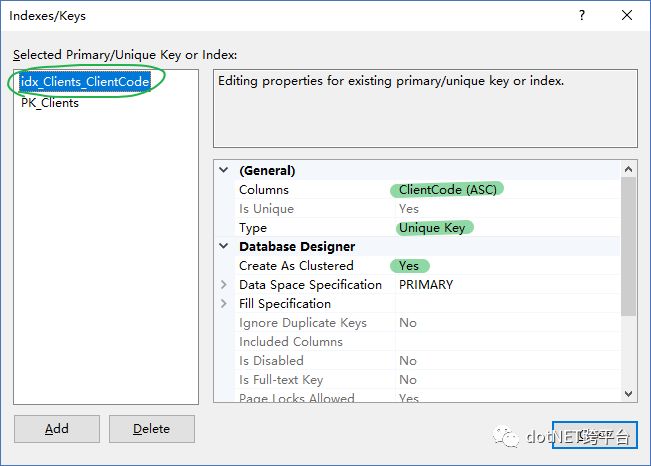
ClientContactInfo 表的索引
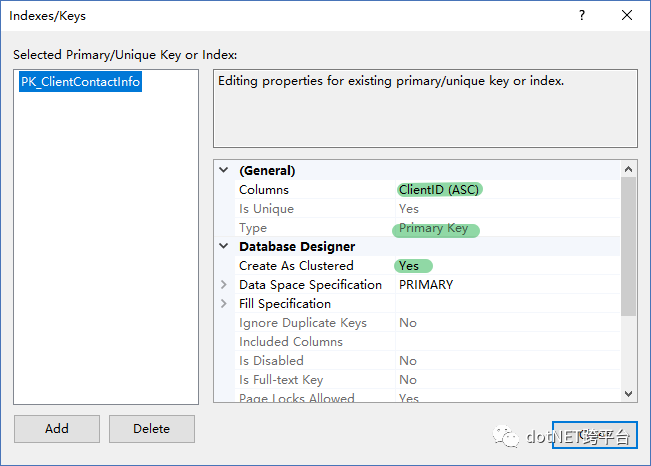
外键FK_ClientContactInfo_Clients的设置
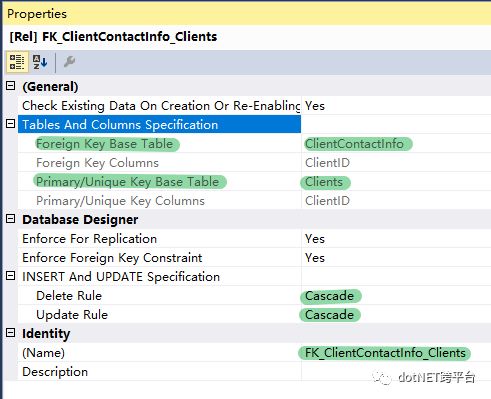
如何用EF5/6实现 Entity Split
首先让我们先来看看 EF5/6 是怎么实现的。
如果用EF5/6的话,这个很简单。因为有设计器啊,TableMapping就可以轻松搞定。
项目文件:
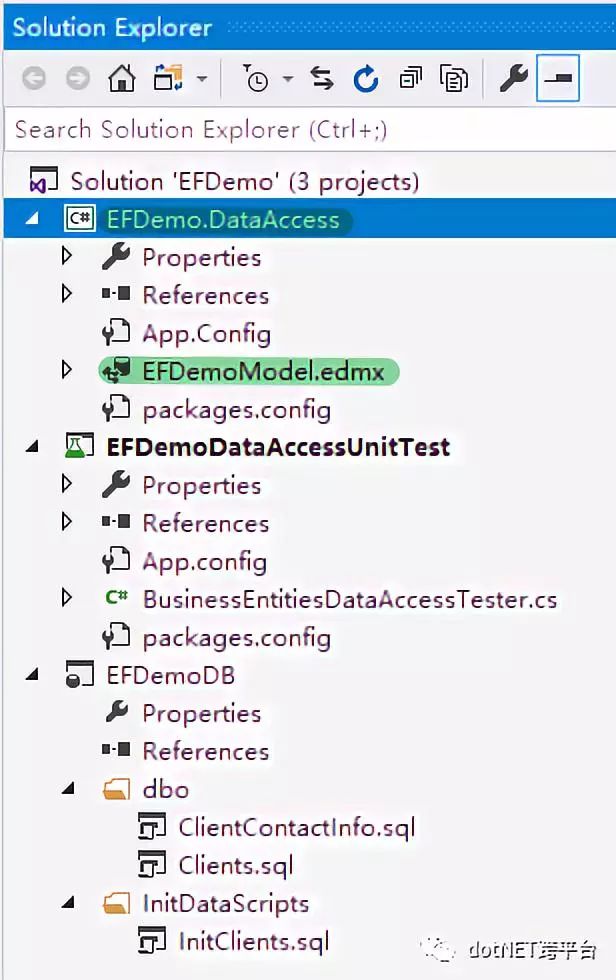
EF Diagram:
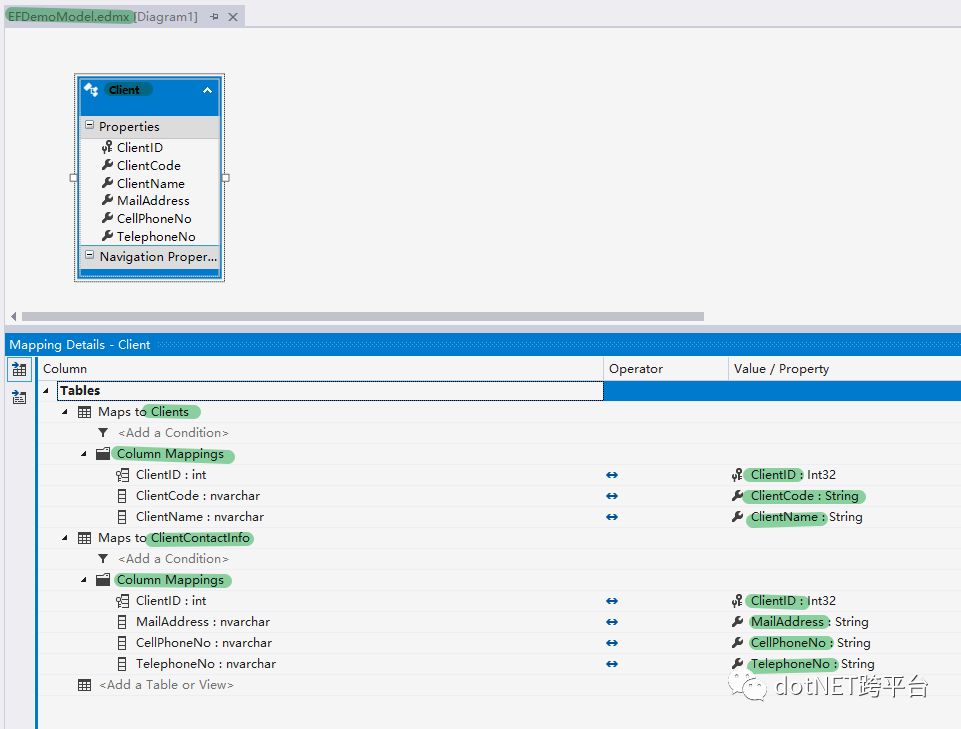
UnitTest程序:
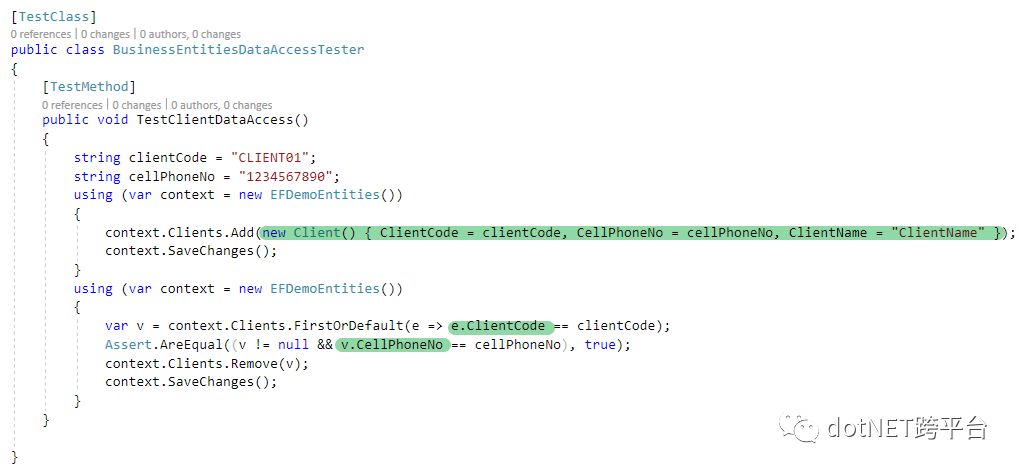
看,程序完全不需要考虑数据是来源于不同的两个数据表。简单吧?
如何用EFCore 实现 Entity Split
用EF Core,没有设计器,怎么搞?其实,就算有设计器,也不能和EF5/6那样的实现方式的。
这里我们需要先请出 EF Core的一个重大功能 Lazy Loading。这个功能从EF Core V2 开始支持。
EF Core Lazy Loading
文档:https://docs.microsoft.com/zh-cn/ef/core/querying/related-data#lazy-loading
它有两种实现方式,
一种是用Microsoft.EntityFrameworkCore.Proxies包,以及调用UseLazyLoadingProxies来启用这个包。并且要求类里面的NavigationProperty需要是public且virtual
另外一种使用 Microsoft.EntityFrameworkCore.Abstractions 包中定义的 ILazyLoader 服务的引用。这个需要类里面做更多的特定代码来支持
上述两种做法各有利弊,所以我们接下来会针对两个做法都分别用一次。用它们来实现 基于 EF Core的Entity Split
可行性分析
通过上面分析的EFCore里面ToTable的做法,我们知道,实际上是真的不可避免地需要有俩 Entity ,这样才可以设置它们分别映射到不同的数据表。然后,因为有了Lazy Loading,我们可以对 Client 这个 主类 ,添加引用 ClientContactInfo 类的相应的几个属性。通过玩弄getter和setter的把戏。让EFCore的Lazy Loading在getter/setter调用到ClientContactInfo的属性的时候,按需装载,这样又可以实现Entity Split,系统性能也得到好处。
用Microsoft.EntityFrameworkCore.Proxies来实现EFCore的Entity Split
项目文件:
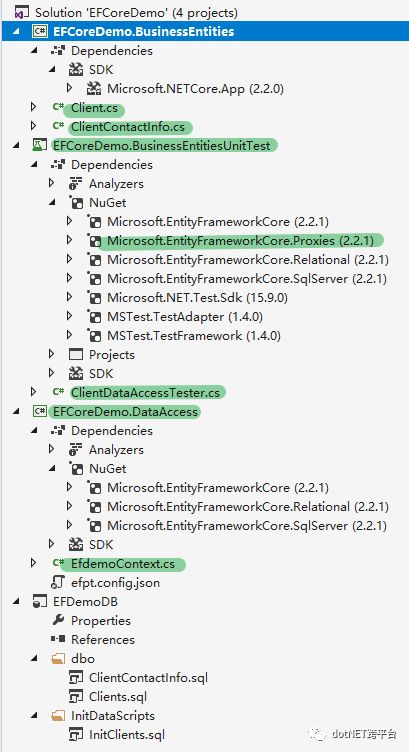
程序:
DbContext:

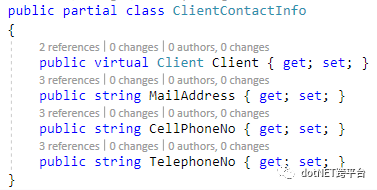
ClientContactInfo:
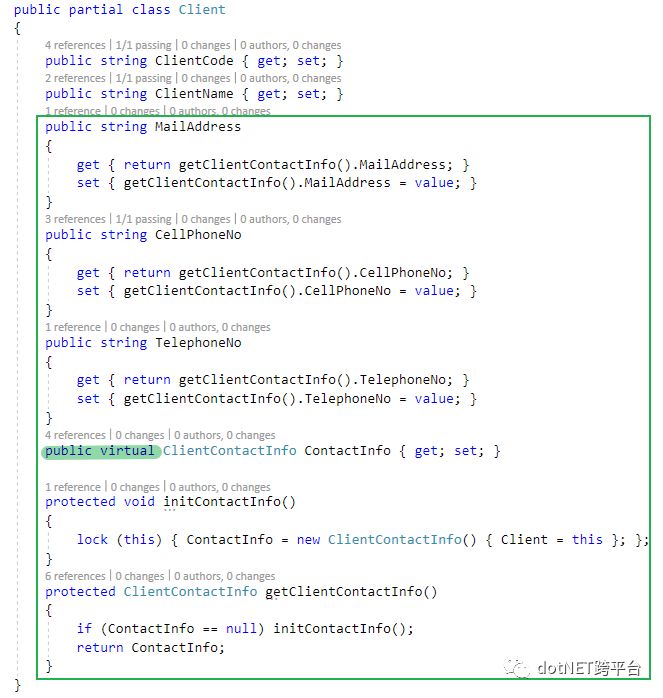
Client:
UnitTest:
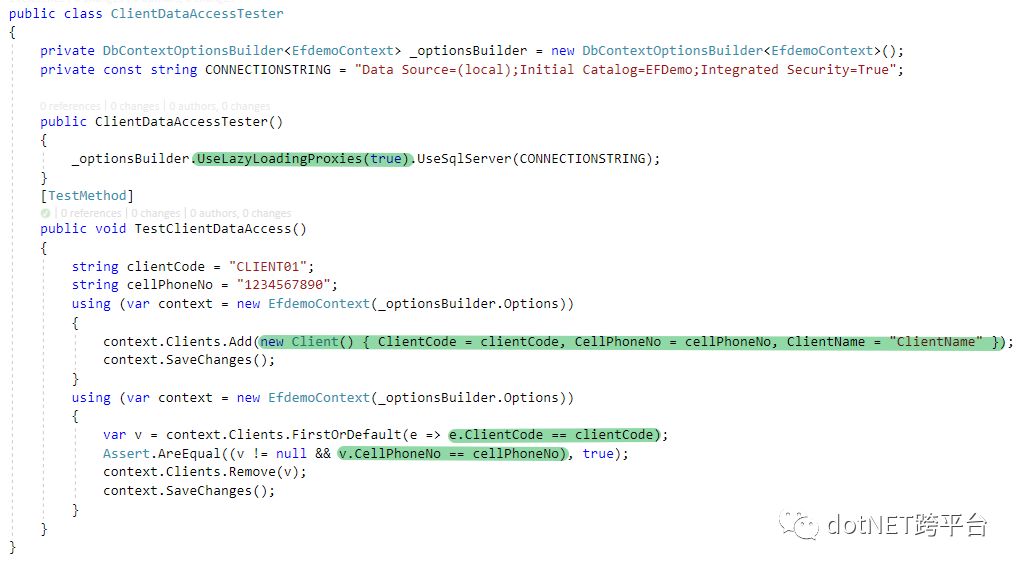
看上面UnitTest的程序,就看出来,我们程序调用Client的时候,完全不需要考虑数据是来源于不同的两个数据表。Entity Split就这样搞定了。
用Microsoft.EntityFrameworkCore.Proxies的缺点是,我们需要有Client.ClientContactInfo这个NavigationProperty。而且还有另外一个可能的坑(如果你尝试调用Client.ClientContactInfo.GetType()就知道了,这个我们可以以后再特别弄个随笔来吐槽一下)。
接下来,为了维持OOP的美式咖啡口味,让我们换个Lazy Loading的实现方法。
用Microsoft.EntityFrameworkCore.Abstractions来实现EFCore的Entity Split
项目文件:
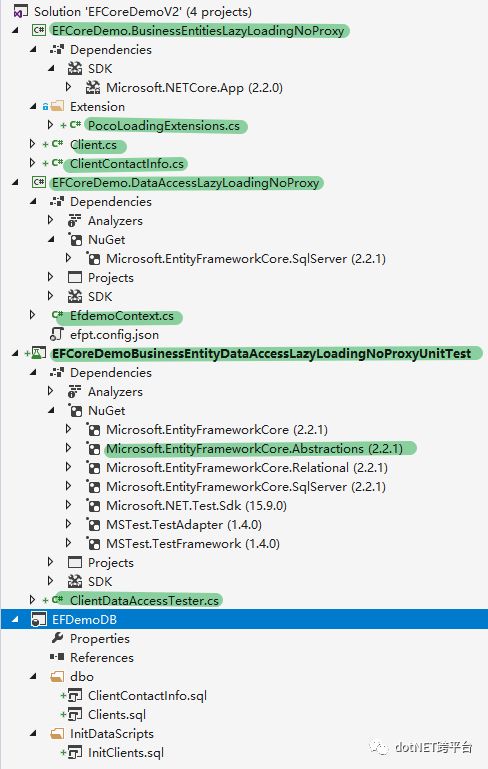
程序:
DbContext (这个和上面那个例子一样,就不骗篇幅了,大家继续参照上面那个Lazy Loading做法的贴图就好)
ClientContactInfo(这个和上面那个例子一样,就不骗篇幅了,大家继续参照上面那个Lazy Loading做法的贴图就好)
PocoLoadingExtensions (这个是直接抄微软文档上的,所以我也不骗篇幅,大家直接参阅上述微软文档的内容就好。网页上查找一下PocoLoadingExtensions这个文本就能找到了)
Client:
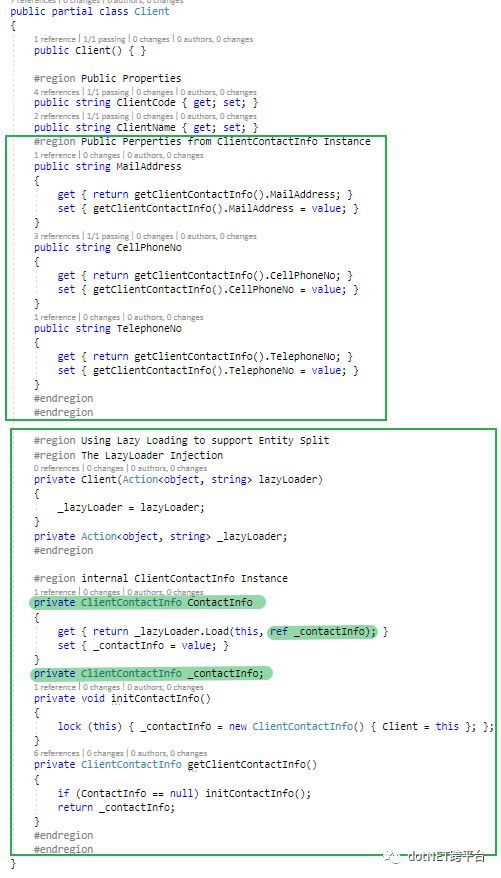
程序里面用了一个private field来存放 ClientContactInfo的 实例,然后用了一个private的ClientContactInfo的property(通过继续玩弄它的getter/setter的把戏来帮忙提高程序的可维护性)UnitTest(这个和上面那个例子一样,就不骗篇幅了,大家继续参照上面那个Lazy Loading做法的贴图就好)
用Microsoft.EntityFrameworkCore.Abstractions的缺点是,我们的类里面需要加入一些额外的程序(为了支持ILazyLoader )。但是好处是,Client的public属性里面,再也没有ClientContactInfo这种NavigationProperty了。就真的是毫无痕迹地实现了Entity Split。
结语
怎么样?EF Core真的很棒,对吧?借助Lazy Loading的功能,我们花费了一些周折,如此简单地实现了Entity Split。
当然,我本人还是希望Entity Split这个可以built-in为EF Core的一个基本功能,而不是采取借助Lazy Loading这样的Walk Around做法。也许接下来的第N个版本,它就会实现的。毕竟"面包会有的,牛奶会有的,一切都会有的。" :-P
下一篇,让我们继续讨论,如何借助Lazy Loading,在用EF Core的Inheritance功能的时候,继续保持数据表的清洁(不需要有冗余的字段)。敬请期待噢。 :-D
相关文章:
Shadow Properties之美(一)【Microsoft Entity Framework Core随笔】
Shadow Properties之美(二)【Microsoft Entity Framework Core随笔】
“幕后英雄”之Backing Fields【Microsoft Entity Framework Core随笔】
原文地址:https://www.cnblogs.com/fatkent/p/10365659.html
.NET社区新闻,深度好文,欢迎访问公众号文章汇总 http://www.csharpkit.com 
div373(div2))




)



)
![AT5147-[AGC036D]Negative Cycle【dp,模型转换】](http://pic.xiahunao.cn/AT5147-[AGC036D]Negative Cycle【dp,模型转换】)



)
![pjudge#21652-[PR #4]到底有没有九【数位dp】](http://pic.xiahunao.cn/pjudge#21652-[PR #4]到底有没有九【数位dp】)


)
 报文类)