前言

我们都知道，API网关是工作在应用层上网关程序，为何要这样设计呢，而不是将网关程序直接工作在传输层、或者网络层等等更底层的环境呢？让我们先来简单的了解一下TCP/IP的五层模型。

 

 

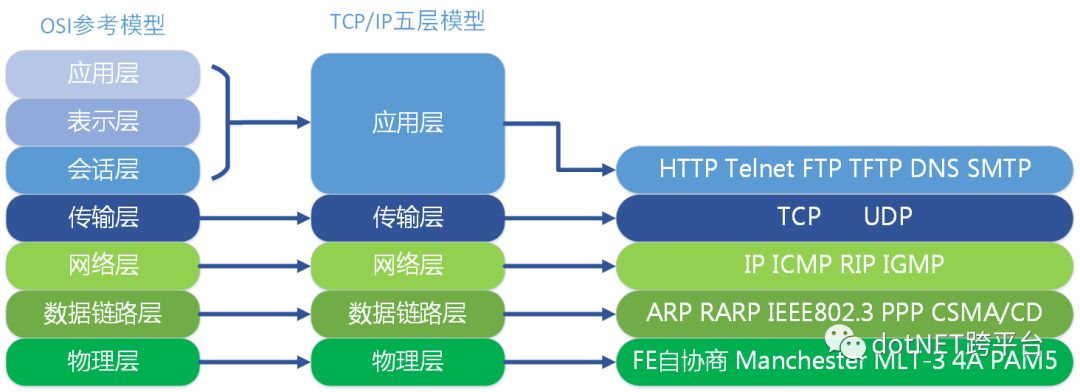
（图片出自http://www.cnblogs.com/qishui/p/5428938.html）

 

具体的每一层的工作原理想必大家都已经滚瓜烂熟了，笔者也不在重复的复述这内容。回到上面的问题，为何API网关需要工作在应用层上的问题就变得一目了然，物理层面的网关是交给物理设备进行的，例如物理防火墙，而HTTP是网络通信中已经完全规范化和标准化的应用层协议，随处可见的通信协议，当然，你把网关集成到FTP上面也可以，增加相应的协议转换处理即可。

回过头来，RPC是什么，是一个协议吗？不是。确切的说它只是“远程调用”的一个名称的缩写，并不是任何规范化的协议，也不是大众都认知的协议标准，我们更多时候使用时都是创建的自定义化（例如Socket，Netty）的消息方式进行调用，相比http协议，我们省掉了不少http中无用的消息内容，例如headers消息头。本一个简单的GET请求，返回一个hello world的请求和响应，元数据就10个字节左右，但是加上headers消息头等等http的标准内容，估计会膨胀到25~30个字节，下面是一个常见的http的headers消息头。

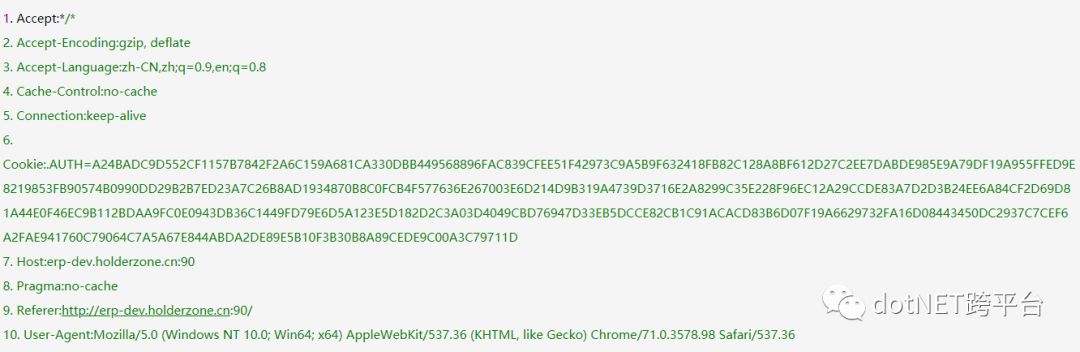
因此很多系统内部调用仍然采用自定义化的RPC调用模式进行通信，毕竟速度和性能是内网的关键指标之一，而标准化和语义无关性在外网中举足轻重。所以，为何API网关无法工作在RPC上，因为它没有一个像HTTP/HTTPS那样的通用标准，需要我们将标准化的协议转为为自定义协议的处理，通常称为Relay，如图所示。

 

 

 

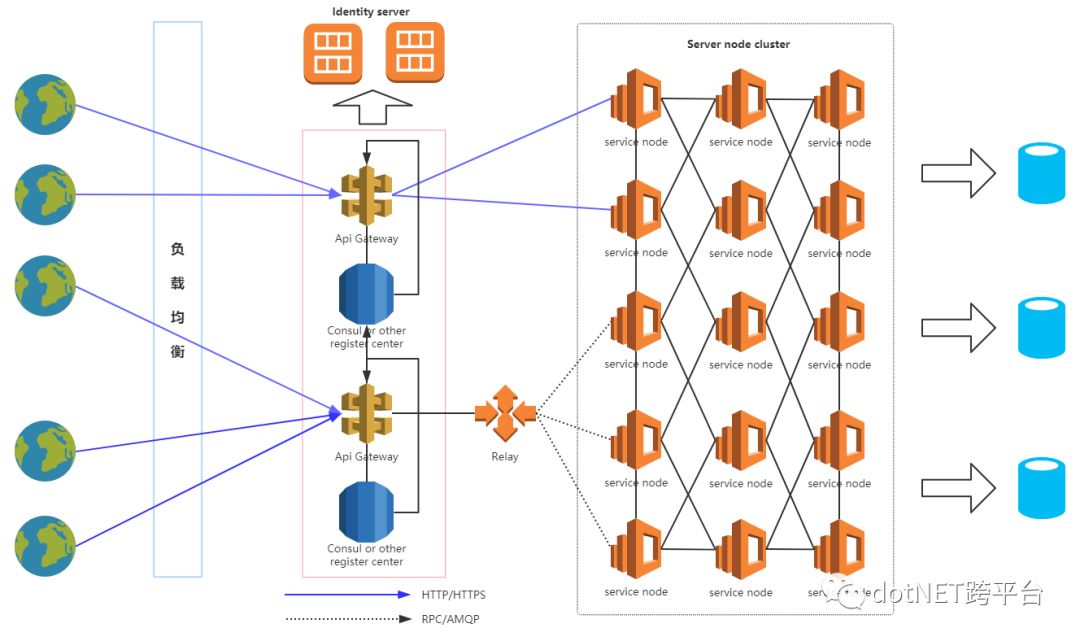
上一篇中，我们已经简单的介绍了Ocelot在Http中的网关实现，无需任何修改，全都可以在配置文件中完成，相当方便。但是，我们需要实现自定义的RPC协议时，应该怎么办呢？

这里，感谢张队在上一篇中提供建议和思路https://www.cnblogs.com/SteveLee/p/Ocelot_Api_http_and_https.html#4171964，可以通过增加（或扩展）OcelotMiddleware来处理下游协议的转换。

 

 

（图片出自https://www.cnblogs.com/shanyou/p/7787183.html）

 

Ocelot下游中间件扩展

我们知道，在Ocelot网关中，所有操作均通过中间件来进行过滤和处理，而多个中间件之间的相互迭代通信便形成了Ocelot的通信管道，源码中使用OcelotPipelineConfiguration来扩展和配置更多的Ocelot中间件，见源码所示：

 

 

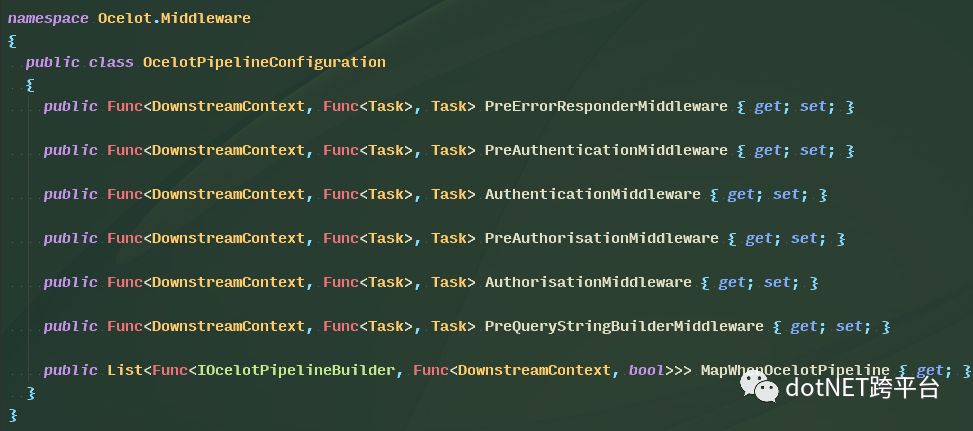
在源码中，我们可以看到，所有的中间件对应操作对象的均是DownstreamContext下游上下文对象。而MapWhenOcelotPipeline正好可以满足我们扩展中间件的需求，它提供List<Func<IOcelotPipelineBuilder, Func<DownstreamContext, bool>>>委托以供我们配置多个下游处理中间件并映射到Ocelot管道构建器中。我们查看DownstreamContext的源码，可以看到，构建下游上下文的时候，默认就传递了HttpContext对象，而通过DownstreamRequest和DownstreamResponse完成对下游的请求和响应接收。

 

 

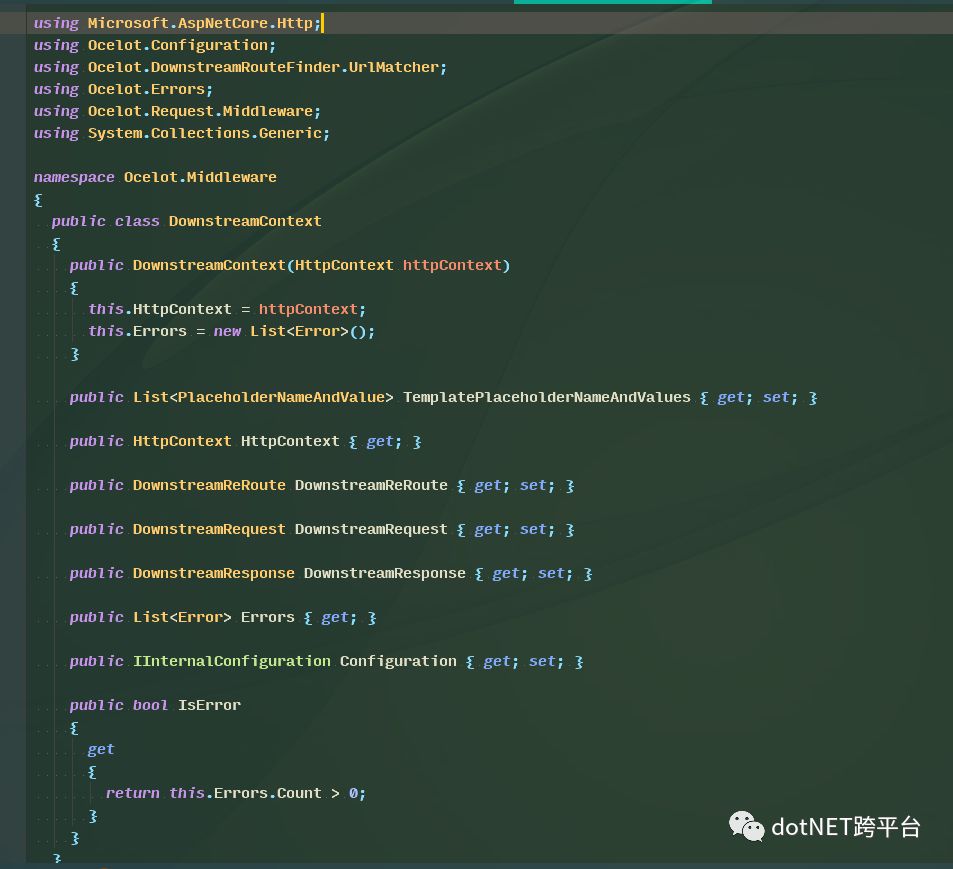
这样，我们便可以通过对OcelotPipelineConfiguration的扩展来添加自定义中间件，我们把它扩展名称定义为OcelotPipelineConfigurationExtensions吧。

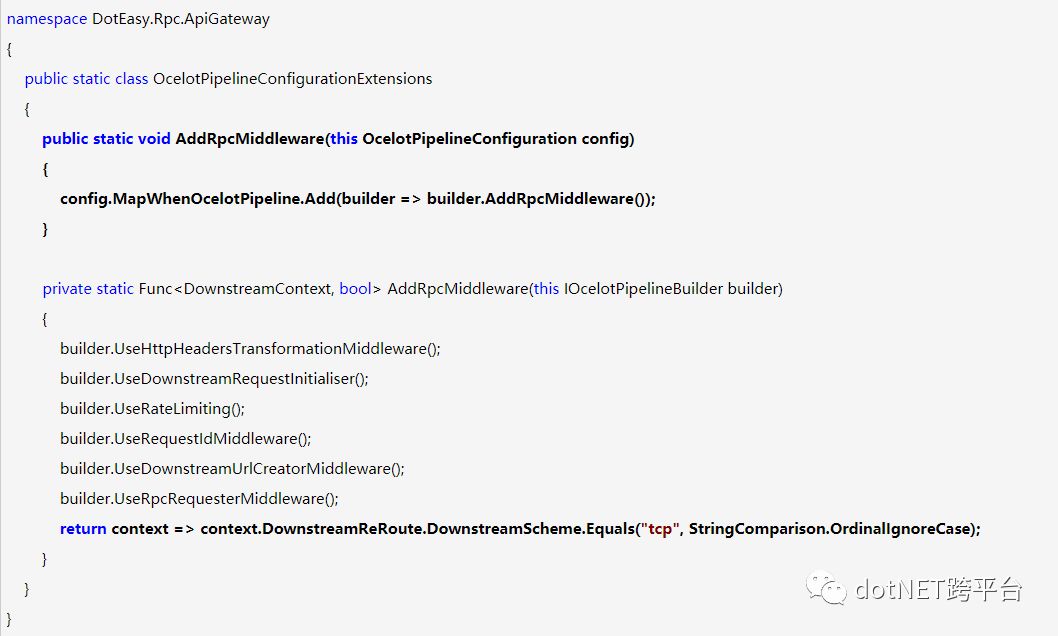
当有了DownstreamContext的扩展定义，而且在下游配置中，我们需要指定的配置协议是tcp，那么我们便可以开始实现这个扩展的中间件了，我们把中间件的名称定义为RelayRequesterMiddleware。

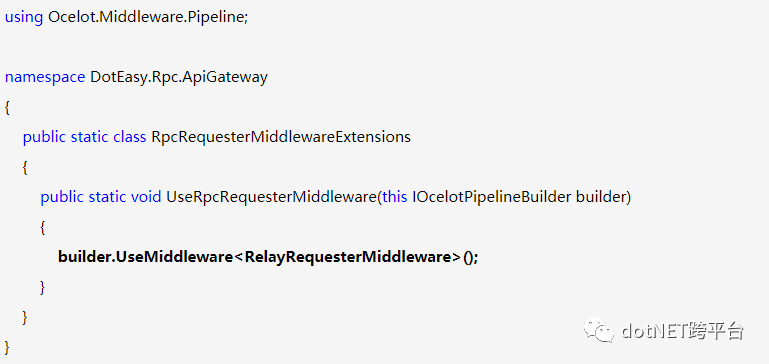
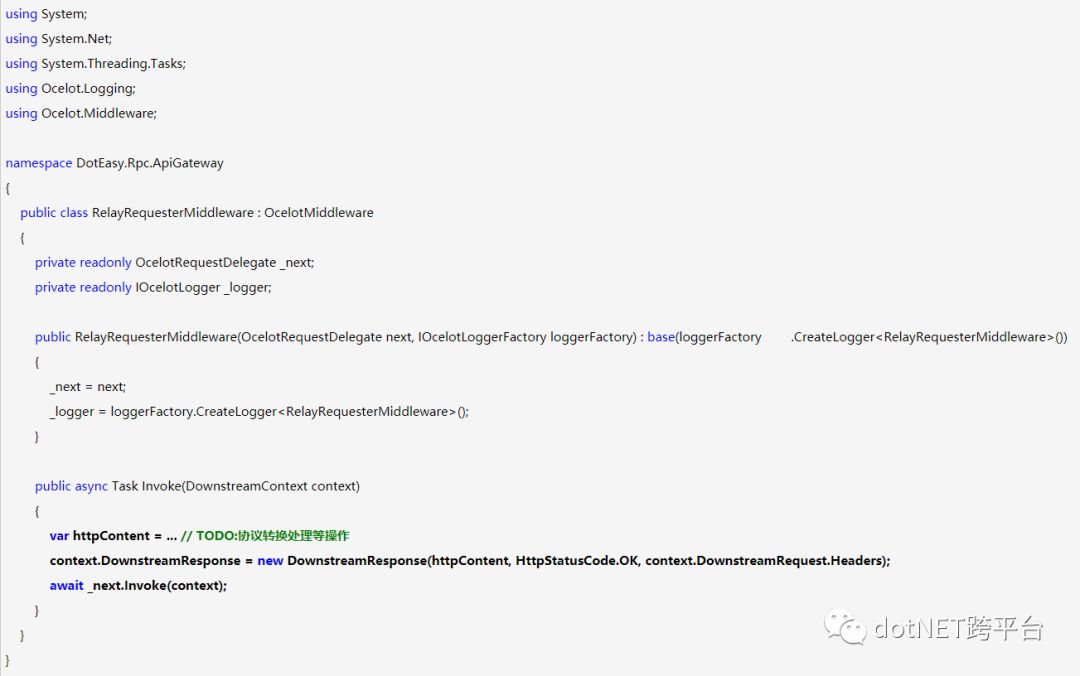
上面加粗的代码便是下游拦截的主要处理地方，在这里我们便可以使用http转rpc的协议转换处理。当然，在Ocelot的使用配置中，我们需要对该Middleware中间件进行添加。

 

app.UseOcelot(pipelineConfiguration => pipelineConfiguration.AddRpcMiddleware()).Wait();

 

以上便完成了对Ocelot中DownstreamContext的扩展，

总结下来，当我们需要扩展下游协议时，我们需要手动配置OcelotPipelineConfiguration并添加到IOcelotPipelineBuilder中，然后通过扩展IOcelotPipelineBuilder实现下游中间件的自定义处理。

 

手动协议转换

其实到上面这一小节，相信很多朋友都可以实现自定义的下游拦截和处理了，而本节的介绍，只是针对在Doteasy.RPC中如何进行协议转换的一个参考。

 

我们先看一组http中的URL：http://127.0.0.1:8080/api/values，然后再看看tcp中的URL：tcp://127.0.0.1:8080/api/values。有什么区别吗？没有任何区别，唯一的区别是scheme从http转为tcp。而在rpc过程调用中，一般我们是没有“绝对路径+谓词”的方式去识别服务节点的，一般都是tcp://127.0.0.1:8080，而具体指定的服务节点交给注册中心去完成，也就是通常所说的服务发现。

由于Doteasy.RPC内部并未实现如“<scheme>://<username>:<password>@<host>:<port>/<path>......”这样标准化的统一定位，所以笔者的做法是将RPC的客户端集成到Ocelot宿主中，让它替代DownstreamConext下游的请求和响应，通过扩展反射的方式实现所有代理的生成，并根据谓词和参数进行方法的调用，这样，代码就不需要做太多的修改。

首先需要明白这样做的一个目的

1. 在Doteasy.RPC单次调用中，为了减少众多接口生成代理所带来的耗时，每次调用前都会检查相关接口的动态代理是否已经生成，确保每次只生成一个片段的代理。然而，作为一个网关中的中继器，这样一次生成一个代码片段显得非常无力，需要将所有的接口全部生成代理，以方便在Relay中查找和调用。

2. 再看一个RESTful风格中的URL：http://127.0.0.1:8080/api/1/Sync，一般我们将谓词放置最后，而参数一般放置在谓词的前面，在手动转换RPC的过程中，就可以利用谓词来假设我们需要调用的RPC服务名称（但实际不一定就是Sync）。

3. 基于Doteasy.RPC中的服务容器，可以很方便的实现参数类型转换以及后期的Headers处理。

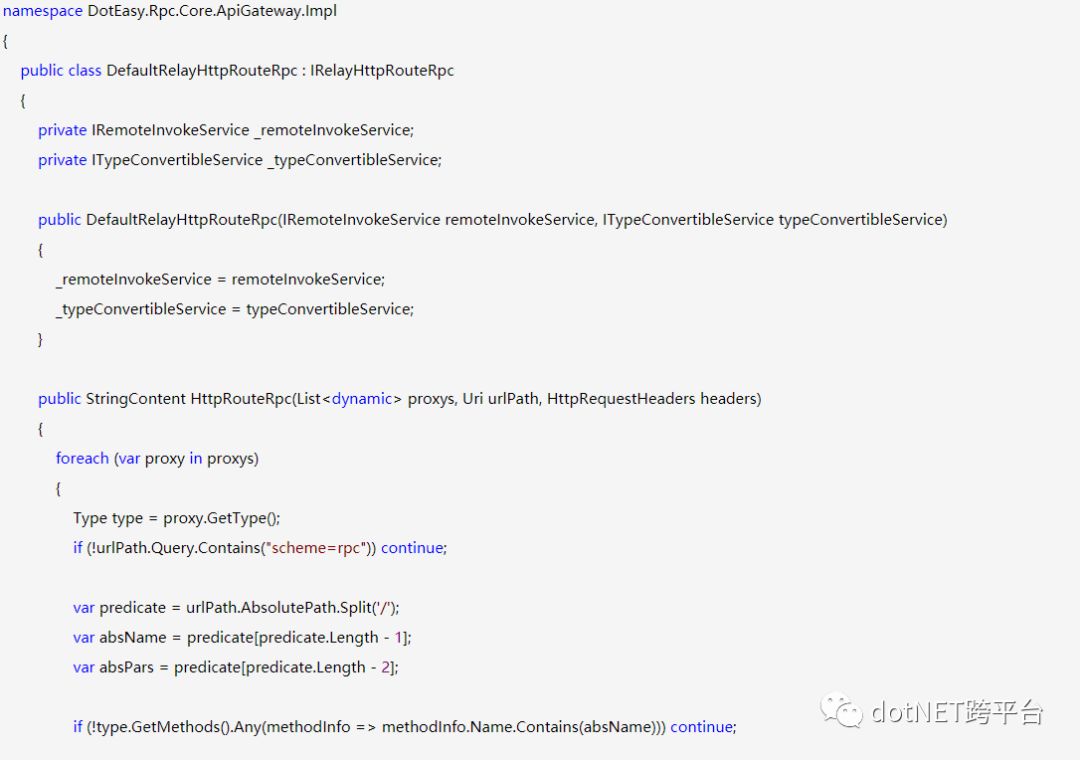
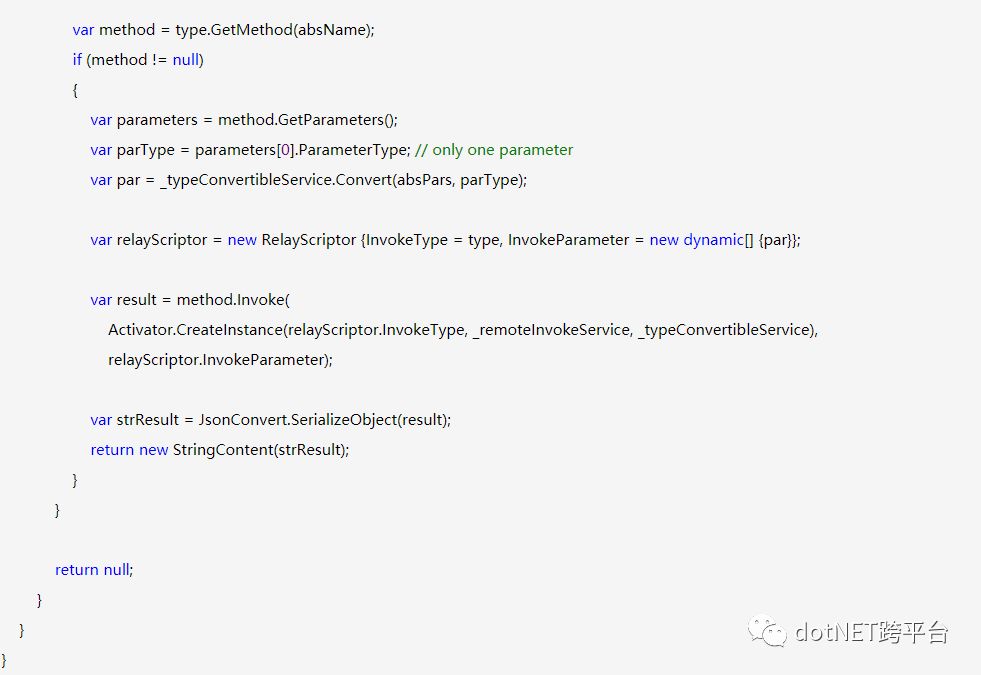
笔者的转换方式是将谓词作为服务名称和参数值进行调用，虽然这种方式目前来看十分拙劣，但为自定义转换提供了一组思路，还可以不断的优化和调整，目前缺点如下：

1. 当http中多个参数时，无法进行协议转换，因为不知道代理目标方法的参数集合是多少，只有全局假设一对一的参数目标。

2. RPC客户端在网关中集成了大量的代理生成，无法实现动态更新，例如原来手动替换DLL，接口自动更新动态代理。

3. 每一次调用都需要从大量的代理中查找指定（或模糊匹配）的方法名称，如果存在1KW+的接口名称，这个查找将是一个非常严重的瓶颈。

 

总结

世上没有100%完美的事物，所以才有各种各样的手段，这里笔者在Doteasy.RPC和Ocelot的基础上做了一个简单下游协议转换，有兴趣的朋友可以自行实现自己想要的协议转换。再次感谢张队提供的Ocelot手动转RPC思路。

原文地址：

https://www.cnblogs.com/SteveLee/p/Ocelot_Api_http_route_RPC.html

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com