D - ABC Conjecture Gym - 102798D

题意：

规定rad(n)=n的所有质因子的乘积
给你一个c，问能否构造a和b使得a+b=c且rad(abc)<c

题解：

先说结论，如果c可以拆分出两个一样的质因子，则能构造a和b
即 n=p1^a1 * p2^a2 . . .*pn^an,
a1到an有一个>=2即可
为什么？
首先如果a1到an都是1，那rad©=c,那么rad(abc)不可能小于c
如果a1到an存在一个>=2，怎么能够说明rad(abc)<c?看下图

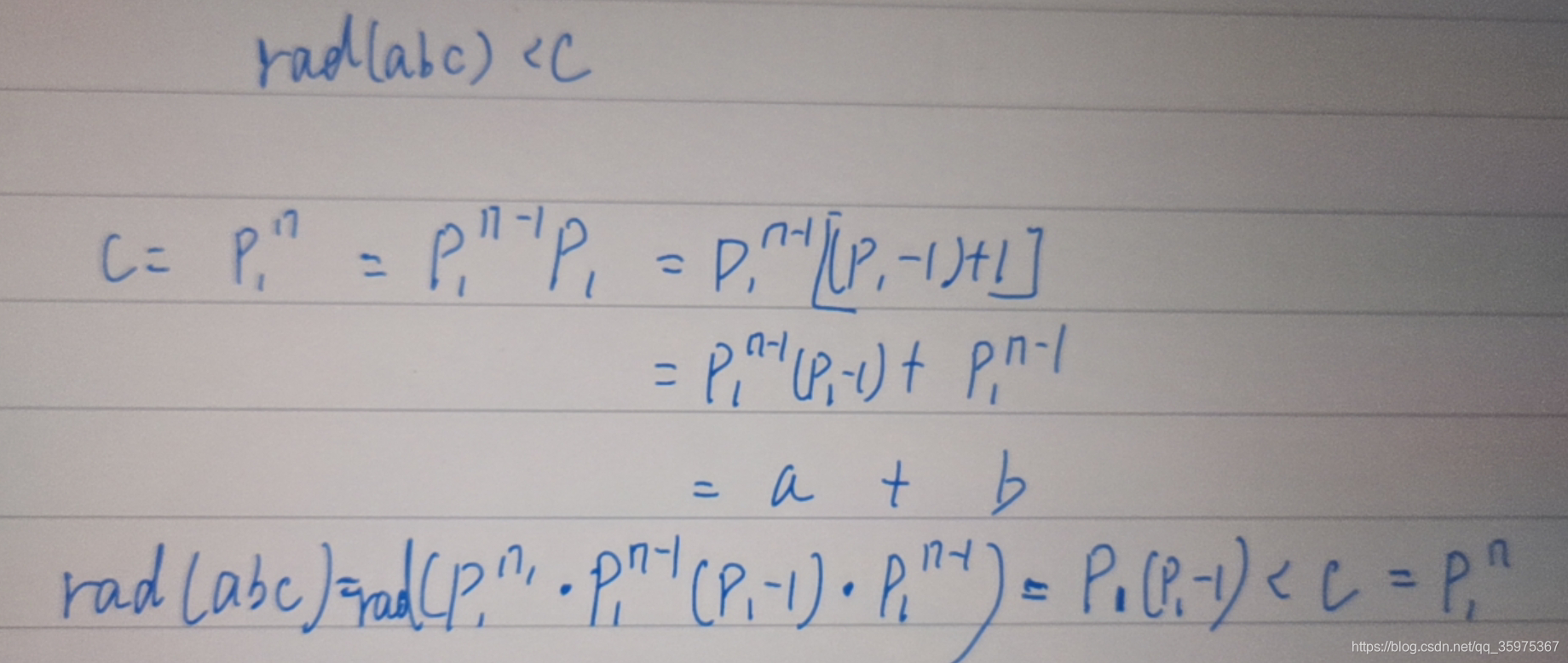
看本题，1<=c<=1e18
线性筛可以晒出1e7以内，那么也就是可以解决[1,1e14]以内的c，那1e14到1e18之间如何解决？
我们想c = P ⁿ *x,n>=2
P为[1e14,1e18]以内的素数,那n只能是2，不然c就超范围了，而x最大也才到1e4，所有我们可以将c先除x，然后看（int）sqrt(c/x) 的平方是否等于c/x，相当于反向验证了是否存在P
详细看代码：

代码:

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e7;
int prime[maxn+1];
bool vis[maxn];
void getprime()
{vis[1]=1;for(int i=2;i<=maxn;i++){if(!vis[i])prime[++prime[0]]=i;for(int j=1;j<=prime[0]&&prime[j]<=maxn/i;j++){vis[prime[j]*i]=1;if(i%prime[j]==0)break;}}
}
int main()
{getprime();int t;cin>>t;while(t--){ll x;cin>>x;bool f=0;for(int j=1;j<=prime[0];j++){if(x%(prime[j]*prime[j])==0){f=1;break;}else if(x==1){f=0;break;}else if(x%prime[j]==0)x/=prime[j];}if(f==1)cout<<"yes"<<endl;else if(x==1)cout<<"no"<<endl;else {ll w=sqrt(1.0*x);if(w*w==x)cout<<"yes"<<endl;else cout<<"no"<<endl;}}return 0;
}
/*
54
1000000007
*/