参考文章
详细定义内容看这个参考文章

结论：

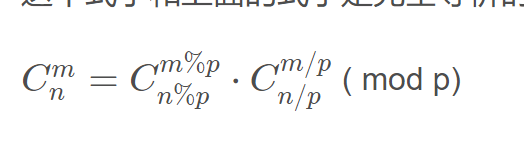
模板：

Lucas函数：

long long Lucas(long long n,long long m){if(m==0)  return 1;return Lucas(n/p,m/p)*C(n%p,m%p)%p;
}

组合数函数：
此处求逆元的用的b^p-2

long long C(long long n,long long m){if(n<m)      return 0;if(m>n-m)     m=n-m;long long  a=1,b=1;for(int i=0;i<m;i++){a=(a*(n-i))%p;b=(b*(i+1))%p;}return a*quickpow(b,p-2)%p;
}

整体代码：

#include <iostream>
#include <algorithm>
#include <cstdio>
using namespace std;long long n,m,p;long long quickpow(long long base,long long power){long long ret=1;while(power){if(power%2)ret=ret*base%p;base=base*base%p;power/=2;}return ret;
}long long C(long long n,long long m){if(n<m)      return 0;if(m>n-m)     m=n-m;long long  a=1,b=1;for(int i=0;i<m;i++){a=(a*(n-i))%p;b=(b*(i+1))%p;}return a*quickpow(b,p-2)%p;
}long long Lucas(long long n,long long m){if(m==0)  return 1;return Lucas(n/p,m/p)*C(n%p,m%p)%p;
}int main()
{int T;scanf("%d",&T);while(T--){scanf("%lld%lld%lld",&n,&m,&p);printf("%lld\n",Lucas(n,m));}return 0;
}

复杂度

O(p * logm * logp)，后者都是常数级别，所以复杂度主要取决于p，p不能太大，一般在10⁵以内即可

优化

由于p已知，所以可以O( p )的处理阶乘，优化常数