AWS vs K8s 是新的 Windows vs Linux

作者：Ian Miell是开源程序员、演讲师、作家和博客写手

以前……

如果你与我一样，年过四十，又在IT行业工作，恐怕还记得每个人使用Windows，一小群但越来越多的人在业余时间埋头编译Linux的年代。

Windows用户见此情形会困惑不解：“明明Windows拥有你需要的一切功能，得到支持，还易于使用，你何必这么做？！”

这个问题的答案可谓五花八门。有些人喜欢捣鼓，有些人希望操作系统“免费”，有些人想要对软件拥有更大的控制权，有些人想要速度更快的系统，所有人都能搬出这么做的某个理由。

现在……

当我又熬夜试图让某个新的Kubernetes附件按文档记载的那样运行时，惊讶地发现我处于与过去颇为相似的境地。就在几年前，Kubernetes本身对于门外汉来说是混乱而恐怖的东西：API经常变更；你试图自行构建，却发觉说明文档编得很差；以及一个不成熟的大型软件项目该有的种种特点。

话虽如此，无论过去还是现在，Kubernetes的治理都比大多数开源软件项目先进得多，不过当时的感觉就如同2000年前后编译Linux，或者处理每当你拔掉USB连线，一半时候崩溃的笔记本电脑（是的，这种事过去常发生）。

就拿knative来说吧：

640?wx_fmt=png

knative俱乐部的第一条规则是，你无法解释knative是什么东东。

我那些使用AWS的同事看到我经常费老大的劲，问道：“明明AWS拥有你需要的一切功能，得到支持，还易于使用，你何必这么做？！”

AWS是Windows

与Windows一样，AWS也是一种产品。它并不灵活，但性能可靠。API得到了明确的定义，关键性能指标（KPI）很好，对于大多数“实际”工作负载来说足够实用。帮助定义你能实现什么、不能实现什么的种种资源方面有限制。

大多数人都想要这样，就像大多数人想要一辆可以跑起来，又不需要常修理的汽车一样。有些人喜欢维修汽车。一些公司聘有机修工来维修一大批汽车，因为规模化后成本较低。同样道理，一些组织切中要点：它们可以看到再度自建数据中心带来的好处。想想Facebook或者完全改弦易辙的Dropbox。（后文会探讨这点）。

与微软一样，AWS采取的做法是拥抱并拓展（embrace and extend），现在谷歌如法炮制，一旦觉得某个领域有利可图，就开发出越来越多的产品。

AWS和Kubernetes

这就引出了AWS与Kubernetes的关系。AWS没有领会Kubernetes的要点，这可不是什么秘密。AWS已经拥有ECS，这是个丑陋又笨拙的产品，不过如果你一开始就在AWS上投入了大成本，它倒是再合适不过。

有人说，不过有EKS。我最近没有关注EKS，该产品很久后才面市，但它根本谈不上功能丰富。给人的感觉就像是一个云框架（AWS）与另一个框架（K8s）联姻，一个难缠的青少年退学了。比如说，继续有人埋怨部署起来“太费时间”。

640?wx_fmt=png

就像微软当初对待Linux，AWS长期无视Kubernetes，而且与微软一样，AWS也被迫对竞争对手采取“拥抱并拓展”的做法来保护市场份额。我经常接触AWS人员，他们在解释我们明明可以用ECS为什么要使用EKS时讳莫如深。

EKS和锁定

这就引出了AWS交付EKS，因而“拥抱”Kubernetes的主要原因之一：身份和访问管理（IAM）。

EKS（同所有AWS服务一样）与AWS IAM高度集成。正如大多数人所知，IAM是AWS锁定的真正根源（而Lambda是出众的锁定技术。）

改变身份管理系统几乎是任何一家企业组织最不想做的事情。要求贵公司的首席技术官主张对核心安全系统进行根本性改变，短期内对公司没有效益，风险又很大，这可不是提升职业生涯的举措。

另一方面，有人对为什么Linux永远不会威胁Windows提出了类似的论点；虽然桌面端确是如此，但手机和Mac的出现已经将Windows沦为消费级计算市场的配角。只要看看在过去的10年微软没有将浏览器强行推给人们就略知一二了。

因此，只要市场上出现一些意想不到的转变，另外某种技术就能受到追捧，成为市场老大。微软清楚这一点，AWS也清楚这一点。这就是为什么微软和AWS不断为各自的解决方案添加新产品和新功能，这就是为什么EKS会问世。

微软最终让这艘巨型油轮掉头驶向云，大力支持开源、Linux和Docker以及能够将IT人员吸引到其服务上的所有技术。哦，你可以使用与贵公司网络一样的活动目录（AD），并将微软Windows许可证转移到云端。第一个是免费的。微软不再关心操作系统。没有人关心，连Red Hat这家以支持与Windows竞争的操作系统为生的公司也不关心。操作系统已死，成了提供的剩余价值越来越少的大路货。

Kubernetes会迫使AWS将这艘巨型油轮驶向Kubernetes吗？我们可以预料它会拥抱Istio和Knative以及此后出现的任何框架进入到它的解决方案中吗？

AWS的竞争和成本

我不知道。但下面有另外几个原因解释它可能会这么做。

与Windows操作系统鼎盛时期的微软一样，AWS只有一个竞争对手：私有数据中心。就像微软当时的竞争对手（Linux）一样，接纳这个竞争对手很痛苦，成本昂贵，而且风险颇大。

但那个数据中心的操作系统又是什么呢？在Kubernetes出现之前，答案应该是OpenStack。OpenStack被广泛认为很失败，不过凭我的经验，它在大型企业组织中还活着（即便日子不是过得很滋润）。我不是OpenStack的专家，不过据我所知，它无法满足在它需要运行的所有基础设施上成为一种稳定产品，并成为大众化产品所需要的全部条件。这同样是微软在过去面临的情况：你可以在“任何”PC和“任何”硬件上运行，它会“工作”。苹果以限制和控制硬件（并在此过程中获得可观的利润）来应对。Linux有强大的社区支持，它最终满足了对其使用场合来说足够有用的条件。

OpenStack还没有抵达成功彼岸，它试图一蹴而就，不过它嵌入得足够深，对不想被云提供商锁定的那些企业组织而言已成为Kubernetes安装的默认基础。

值得关注的是，AWS提出私有云失败的原因对它自己来说同样适用：企业无法适当地管理弹性需求，无论在自己的数据中心还是掏钱请别的公司打理。指挥与控制式的财务治理结构根本不会在一夜之间改变，以适应敏捷灵活的资源配置模式。（顺便插一下，如果你想在企业中转变IT，就从财务部门开始。如果能拿下这个部门，就有机会在安全和控制职能部门取得成功。如果你不知道为什么一开始从财务部门开始很重要，必然会失败）。

但企业没有全力投入AWS有其他理由：锁定（见上文）和规模经济。我们前面已经提到Dropbox从AWS迁移到自己的数据中心。

就我使用云服务的经历而言，这里有相似的情况。我本人觉得对我自己的数据而言，云存储仍不是来得更便宜，尽管它有明显的好处（没错，即使我计入了自己的人力和冗余要求）。为什么是这样？有这几个原因：

我拥有设计降低人力成本的解决方案的专长和能力
旋转磁盘的折旧很低（购买2块以上磁盘更是如此），访问速度很快
我有足够多的数据要存储，线性云成本开始显得很昂贵

这些原因（专长、资产价值和数据规模经济）是大企业同样会自己搞的几个原因。这个简略的图表表明了这一点：

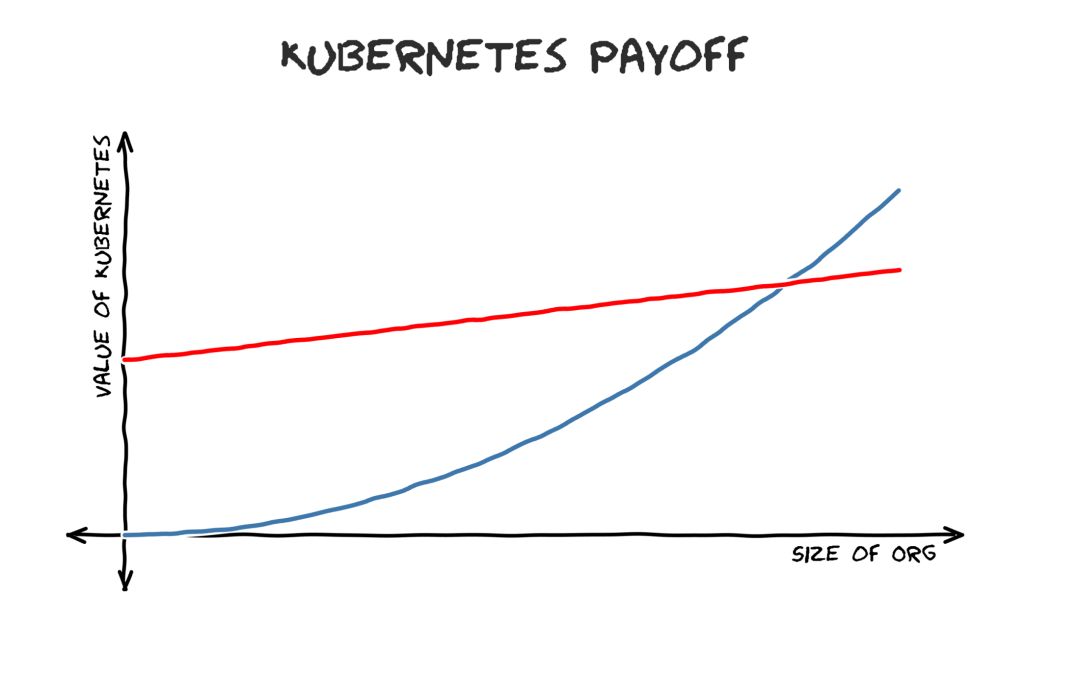
640?wx_fmt=png

红线=运行Kubernetes的成本

运行Kubernetes的零日成本很高（左边红线），但随着你扩展服务，该值呈指数级增长。这就是为什么AWS赚了那么多钱：只要未向你透露其非线性特性，对你用户而言的价值就远高于成本。坦率地说，如果你的规模变得足够大，那么AWS会开始压榨你，但你可能不在乎，因为贵公司在扩展规模。你好比是水里煮的青蛙。等你意识到自己的处境，为时太晚――脱身会很难很难。

AWS和“如果贝索斯失去理智会怎样？”因素

大公司鼎力支持，Linux才真正流行起来。与之相仿，Kubernetes一开始就得到了两家大公司的大笔资金：谷歌和Red Hat。

只有企业组织重视AWS的垄断问题，才会真正取得进展。一些企业肯定重视这个问题，因为监管部门已要求：制定计划，万一贝索斯失去理智，或者亚马逊里面安插了众多俄罗斯间谍，可以在合理的时间里设法迁移。其他原因是，不同的云提供商有不同的优势；随着时间的推移，大企业更有可能同时面对多家提供商。

如果足够多的企业组织这么做，那么AWS基本上无力应对这种威胁。

若使用微软产品，如果你想要其软件，除了乖乖交钱外，别无他路；但如果使用Linux，你其实并不真正被一家提供商牢牢锁定。我见过大企业在谈判期间与Red Hat比胆量，并且投入大量资金调查改而使用CentOS。

出现在Linux身上的一幕出现了在Kubernetes的身上。我们已经看到Kubernetes采用Linux的“发行版”模式：构建了这个平台的精选版，以便更容易使用“特定版本”。早期就有RedHat的OpenShift，它后来改名为“OKD”（我猜是“OpenShift Kubernetes发行版”的意思）。

一些企业会为此付费：让一个庞大的Kubernetes垄断性支持者掌管一切，不过（与Linux一样）总是可以选择换成内部支持或另一家提供商，因为核心系统不归任何人所有。

未来

Kubernetes足够庞大、足够独立才能独自生存。

看看OpenShift以及它如何避免被人说成是Kubernetes的分支。无论是什么样的正当理由，RedHat的抗议并非是不真诚的――他们不仅知道可以在开源基础设施的基础上赚钱，还知道自己也得益于开源基础设施的成功。他们不需要对Kubernetes进行分支。值得关注的，他们的确对Docker进行了分支，甚至在OCI分支之前，这有充分的理由，因为Docker做出的决策显然是为了自身求得生存（比如说，由于“一致性”的原因，硬编码的默认注册中心是Docker自己的）。

Kubernetes则没有这个问题。让我（和其他人）担心的是这个：

640?wx_fmt=png