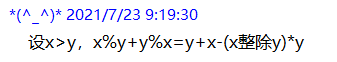
d数组是来算（x整除y）*y中y比x小的数 

 s数组是算（x整除y）*y中y比x大的数

（x整除y）*y    看x对于前面大于他的数是枚举，对于前面小于他的数是d树状数组储存。

d中 x整除y表示x中有多少个y 所以 每个y对于他的倍数都加上y 比如d【y】+y ，d【y*2】+y...d【y*n】+y；当一个比y大的x要求（x整除y）*y的时候就可以根据d【x】来求

{要还是不明白的话就设y=3，x=10 （10/3)*3=9=3+3+3 =d【3】+d【6】+d【9】这真的很巧妙。这样每个数字对于他后面的数字的贡献就可以确定了。就是这个意思。}

那样就看代码吧。

#include<iostream>
#include<cstdio>
using namespace std;typedef long long ll;
const int N=1e6+10;
ll d[N],s[N],ans,sum,num;     //d  s 是上述的意思；  void add(ll *x,int k,int p)
{while(k<N)x[k]+=p,k+=k&-k; 
}
ll ask(ll *x,int k)
{ll ans=0;while(k)ans+=x[k],k-=k&-k;return ans;
}int main()
{int n;scanf("%d",&n);for(int i=0;i<n;i++){scanf("%lld",&num);ans+=1ll*num*i+sum;     sum+=num;ans-=ask(d,num);  //这里是求（x整除y）*y中 小与num的数； for(int j=num;j+num<N;j+=num) //枚举num的倍数 {ans-=1ll*(ask(s,j+num-1)-ask(s,j-1))*j; //枚举num的倍数  s存的是数量，求j-num-1到j-1的数量，这段中那个式子等于j； add(d,j,num);//到时候不懂再说； }add(s,num,1); //num的数量+1； printf("%lld ",ans);}return 0;}