SOS_dp算法

Codeforces博客

简介：

前置知识：状压dp
Sum over Subsets dynamic programming，简称Sos dp,状压dp的一种
用一个列题引出SOS dp：
给你一个由 $2^N$ 个整数组成的确定数组A，我们需要计算对于任意的x， $F (x) = 所有 A [i] 的和 s u m$ 且x&i=i,i是x的子集
整理成公式就是：
$F[mask]=∑i∈maskA[i]F[mask]=\sum_{i∈mask}A[i]$
i∈mask就是&mask=i
F[mask]里面包含了mask所有二进制子集的信息
复杂度为 $O (n * l o g (n))$
$d p [m a s k] [i]$ 表示 $x&mask=x,x∧mask<2i+1x\&mask=x,x^{\land}mask<2^{i+1}$ 的A[x]的和
也就是dp[mask][i]是和mask只有前i个位(最靠右的i位)不同的A[x]的和
转移方程有：
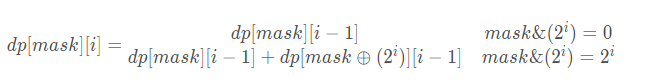
在这里插入图片描述
如图：

可以理解为：每次我求解一个状态时，只从他的所有子集里和他只差一位的状态转移过来
代码：

//iterative version
for (int mask= 0; mask < (1 << N); ++mask) {dp[mask][-1]= A[mask]; //handle base case separately (leaf states)for (int i= 0; i < N; ++i) {if (mask & (1 << i))dp[mask][i]= dp[mask][i - 1] + dp[mask ^ (1 << i)][i - 1];elsedp[mask][i]= dp[mask][i - 1];}F[mask]= dp[mask][N - 1];
}//memory optimized, super easy to code.
for (int i= 0; i < (1 << N); ++i)F[i]= A[i];
for (int i= 0; i < N; ++i){for (int mask= 0; mask < (1 << N); ++mask) {if (mask & (1 << i))F[mask]+= F[mask ^ (1 << i)];}
}